计数类DP——整数划分

//背包：容量是n的背包，n个物品的体积分别是1，2，3……n，恰好装满背包的方案数，每个物品可以用无限次

状态表示：f(i, j)

集合：从1~i中选，体积恰好是j的方案

属性：数量

状态计算：

f（i，j)：i选了0，1，2，3……n个: f[i - 1][j], f[i-1][j-i], f(i-2, j - 2i), f(i-1,j-si)

从1~i中选，选了2个i，并且和恰好为j

从1~i-1中选，和为j - 2r

……

f[i][j] = f[i-1][j] + f[i-1][j-i] + f[i-1][j-2i] + …… +f[i-1][j-i*s]

f[i][j-i] =            f[i-1][j-i] + f[i-1][j-2i] +……+ f[i-1][j-i*s]

——> f[j] = f[j] + f[j-i]

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010, mod = 1e9 + 7;

int n, f[N];

int main()
{
    cin>>n;
    f[0] = 1;
    
    for(int i = 1;i <= n; i++)
        for(int j = i; j <= n; j++)
        {
            f[j] = (f[j] + f[j - i]) % mod;
        }
    
    cout<<f[n]<<endl;
}

 

第二种解法：

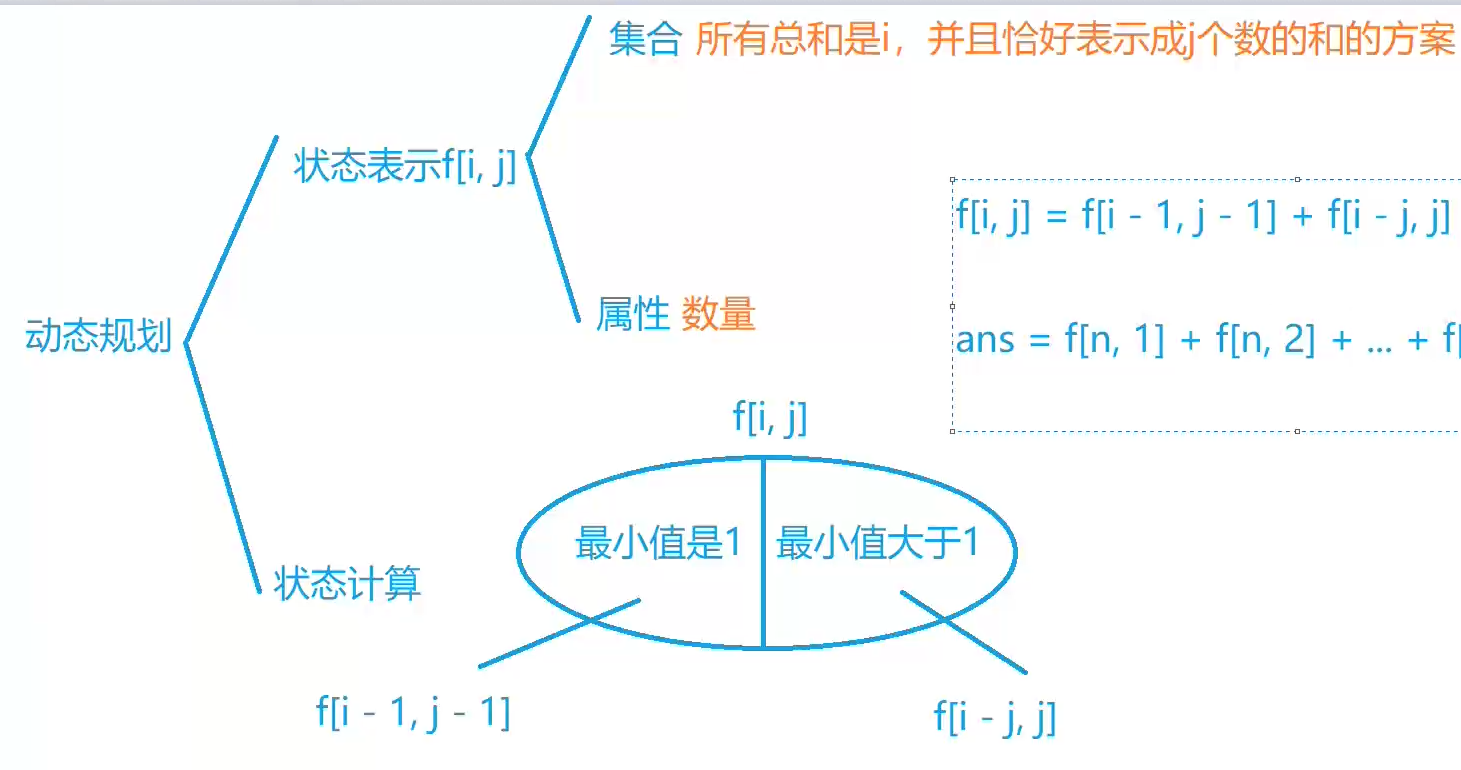
　　所有总和是i，并且可以恰好表示成j个数的和的方案

f(i, j)

方案中最小值是1 ： 把最小值1去掉就是f[i-1][j-1]

方案中最小值大于1: 把每个数都减去1：f[i-j, j]

f[i][j] = f[i-1][j-1] + f[i-j,j]

ans = f[n][1] + f[n][2]……f[n][n]

完全背包的状态转移方程是：f[i][j] = f[i-1][j] + f[i][j-i]

 

 

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010, mod = 1e9 + 7;

int n, f[N][N];

int main()
{
    cin>>n;
    f[0][0] = 1;
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= i; j++)
        {
            f[i][j] = (f[i-1][j-1] + f[i-j][j]) % mod;
        }
    
    int ans = 0;
    for(int i = 1;i <= n;i++)
        ans = (ans + f[n][i]) % mod;
        
    cout<<ans<<endl;
}