线性DP-数字三角形，最长上升子序列

    一层一层的，有着近似的线性关系，称为线性DP。

数字三角形：

 

          复杂度：状态数量 * 转移，本题状态数量是n ^ 2 = 500 * 500 = 250000，转移是O(1)的。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 500, INF = 1e9;
int a[N][N], f[N][N];
int main()
{
    int n;
    cin>>n;
    for(int i = 1;i <= n;i++)
        for(int j = 1; j <= i; j++)
            cin>>a[i][j];
    
    for(int i = 0; i <= n; i++)
        for(int j = 0; j <= i + 1; j++)
            f[i][j] = -INF;
    
    f[1][1] = a[1][1];
    for(int i = 2; i<=n;i++)
        for(int j = 1;j<=i;j++)
        {
            f[i][j] = max(f[i-1][j-1] + a[i][j], f[i-1][j] + a[i][j]);
        }
    
    int res = -INF;
    for(int i = 1;i<= n;i++)
        res = max(res, f[n][i]);
    cout<<res<<endl;
        
}

1、因为有负数，所以不能默认就初始化为0，0不能作为最小数来进行比较。

2、初始化为负无穷的时候多初始化一列，因为到下一行最后一列的时候，f[i-1][j]的j实际上是上一行的i+1列。而第一行第一列的时候上一行的f[i-1][j-1]都是为0，所以赋值虽然是从1开始，但是初始化要从0开始，并且多一个结束。

从下至上：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 500, INF = 1e9;
int a[N][N], f[N][N];
int main()
{
    int n;
    cin>>n;
    for(int i = 1;i <= n;i++)
        for(int j = 1; j <= i; j++)
            cin>>a[i][j];
    
    for(int i = 0; i <= n; i++)
        for(int j = 0; j <= i + 1; j++)
            f[i][j] = -INF;
    
    for(int i = 1; i <= n; i++)
        f[n][i] = a[n][i];
    for(int i = n-1; i >= 1; i--)
        for(int j = 1; j<=i; j++)
        {
            f[i][j] = max(f[i+1][j] + a[i][j], f[i+1][j+1] + a[i][j]);
        }
    
    cout<<f[1][1]<<endl;
        
}

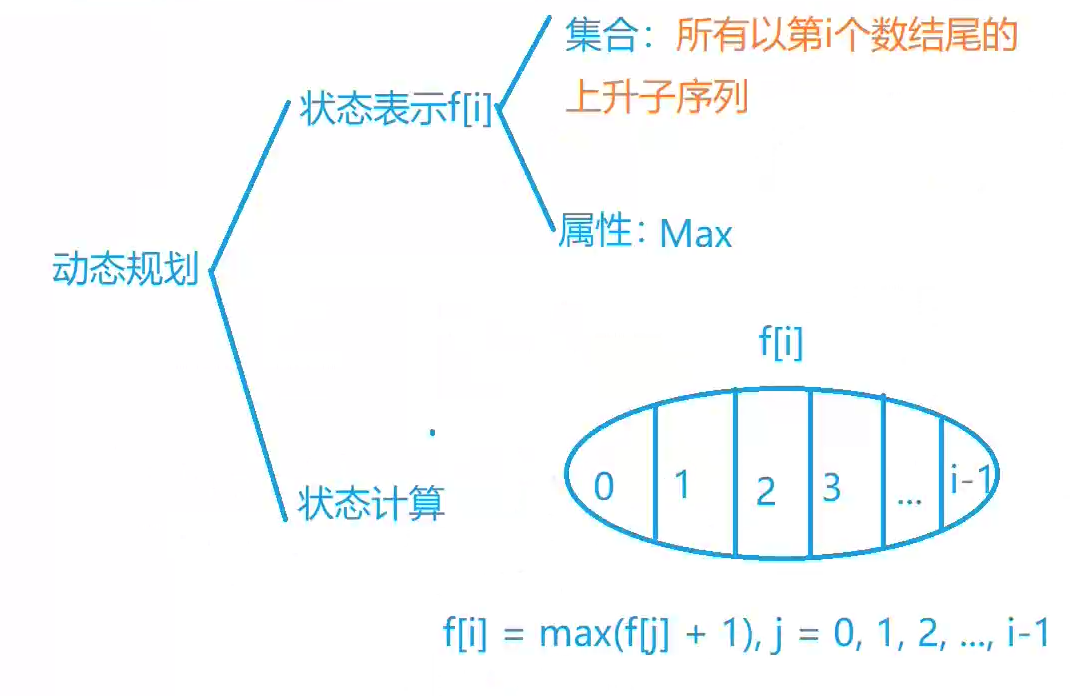
 最长上升子序列：

 

 f[i]: 所有以第i个数结尾的上升子序列的长度，比如以8为结尾的子序列有，1 8，2 8， 1 2 8，1 8， 3 8.

然后整个序列的最大上升子序列就是以每个i结尾的子序列的长度里面的最大值，然后遍历取个max。for(int i = 1;i <= n;i++) res = max(res, f[i]); 

0, 1, 2, 3, ... , i-1, i. aj < ai, f[i] = max(f[i], f[j] + 1);

 

 

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1001;
int a[N], f[N];

int main()
{
    int n;
    cin>>n;
    for(int i = 1; i <= n; i++) {
        cin>>a[i];
        f[i] = 1;
    }
    
    for(int i = 2; i <= n; i++)
        for(int j = i-1; j >= 1;j--)
        {
            if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
        }
    
    int res = 0;
    for(int i = 1;i<=n;i++){
        res = max(res, f[i]);
    }
    
    cout<<res<<endl;
}

也可以上升：

for(int i = 2; i <= n; i++)
        for(int j = 1; j < i;j++)
        {
            if(a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
        }
 时间复杂度：状态数量 * 计算每个状态的转移量，即 n * n;


最长上升子序列 II
如果数据范围N<=100000, 那么上面的复杂度不满足要求。
 优化：

 

 比如以一开始の3和1最长序列都是1，那么如果后面的数能够跟在3后面，那它也一定可以跟在1后面，1比3更小更优，3就可以不用存了，只保留1即可，单调队列优化。当求f[i]时，先计算i，首先计算前面的长度为1的只要保留数最小的那一个即可，长度是2的也只保留第二个数最小的那个，以此类推……,把每个长度最后值最小的存在一个数组里面。最后结尾的数值应该是严格单调递增的。

求ai的最长上升子序列，那么把ai接到前面能找到的最大小于ai的后面，然后直接放进去替代后面的数。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, INF = -2e9;

int a[N];
int q[N];//所有不同长度的上升子序列结尾数的最小值

int main()
{
    int n;
    cin>>n;
    for(int i = 0;i<n;i++) cin>>a[i];
    
    int len = 0;//数组里面的最大长度
    q[0] = INF;
    for(int i = 0; i < n;i++)
    {
        int l = 0, r = len;
        while(l < r)
        {
            int mid = (l + r + 1) >> 1;
            if(q[mid] < a[i]) l = mid;//找得是小于a[i]的最大值
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];//q[r+1]>=a[i]，不停的保存最小的
        
    }
    cout<<len<<endl;
}