邻接表树和图的基于链表的DFS

 

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010, M = 2 * N;
int n, ans = N;
int h[N], e[M], ne[M], idx;//n个单链表的头h[N];
bool st[N];
void insert(int a, int b)//插入以a为起点指向b的邻接表，插在a指向链表的开始位置h[a]
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int dfs(int u)
{
    st[u] = true;=
    int sum = 1, res = 0;//sum子树节点总数，初始化为根节点自己一个，res表示剩下连通块的大小，即所求
    for(int i = h[u]; i != -1;i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            int s = dfs(j);//以u为根节点子树的大小
            res = max(s, res);//每求得一个子树的大小，放入预定的最小池子里面
            sum += s;//把u的每个子树的大小加到s里面，得到的就是u为根的子树的大小，剩下的就是: n - s
        }
    }
    res = max(res, n - sum);//先求得去掉某一个数 剩余连通块的最大值
    
    ans = min(ans, res);//去掉n个数每一个数之后所剩连通块最大值的最小。
    
    return sum;
}
int main()
{
    memset(h, - 1, sizeof h);
    cin>>n;
    for(int i = 0;i<n-1;i++)
    {
        int a,b;
        cin>>a>>b;
        insert(a, b), insert(b,a);//无向边，需要加入b->a, a->b。
    }
    dfs(1);//假定1位根，搜索起点
    cout<<ans<<endl;
    return 0;
}

 如果在dfs后面加一行打印的话：

9

1 2

1 7

1 4

2 8

2 5

4 3

3 9

4 6

j:  6sum: 1

j:  9sum: 1

j:  3sum: 2

j:  4sum: 1

j:  7sum: 5

j:  5sum: 1

j:  8sum: 2

j:  2sum: 6

4

Program ended with exit code: 0

可以发现根据递归式栈的特点，最后进入的最先算出来，所以是DFS的逆序输出结果。

 

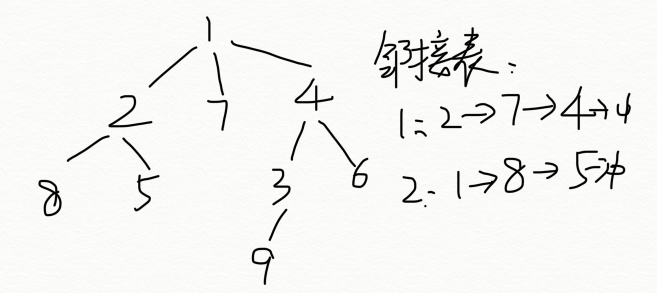
 重心 子树大小 结点

res 8 sum: 1   6

 res 8 sum: 1  9

 res 7 sum: 2  3

 res 5 sum: 4  4

 res 8 sum: 1  7

 res 8 sum: 1  5

 res 8 sum: 1  8

 res 6 sum: 3  2

 res 4 sum: 9  1

4

可以看到打印输出的结果是跟递归的顺序刚好相反的：

递归顺序是：1 2 8 5 7 4 3 9 6 

返回顺序是：6 9 3 4 7 5 8 2 1

子树sum值：1  1 2 4 1  1 1  3 9

然后所求res: 8 8 7 5 8 8 8 6 4 最小的就是4.