trie
在一个字符串集合当中进行字符串的插入和查找，采用的是由上而下的存储从首字母开始的一个树结构。
进行字符串的插入操作：
int insert(char str[]) { int p = 0; for(int i = 0;str[i];i++) { int u = str[i] - 'a'; if(!s[p][u]) s[p][u] = ++idx; p = s[p][u]; } return cnt[p]++; }
我们可以用三个字符串来举例：
1. abcd
2. afce
3. abc
可以这么理解：p代表的是这棵trie数的层数（不一定是层数，当不同延展开来的时候是不同字符串字母散开来的序号编号），从上初始化开始的时候是第0层，每增加一个字符串的一个字母的时候，编号p就+1，p的值最后代表的就是字符串往下延伸了几层（也可能是平行延展，当不同字符串出现时）。真正有意义有值的字符串开始是从1开始的，这棵trie树的root结点是默认为0的位置）那么s[p][u]二维数组的第二维就是代表在这一层上有多少个字符串是以这个字母出发继续延展下去的。s[p][u]代表的是第p层的字母以字母u为分支散开去的序号，因为idx是从0开始，终结的是买个字符串结尾处，即标记每个字符串的位置。
1. abcd这个字符串插入的过程如下：
1）p = 0, u = 0, s[0][0]不存在，那么s[0][0] = ++idx = 1, p = s[0][0] = 1;(s[0][0]指的是以根节点root往下延伸开枝散叶以u为叶子得到的) 'a'
2）u = 1, s[1][1] = 2 = p; 'b'
3) u = 2, s[2][2] = 3 = p;
4) u = 3, s[3][3] = 4 = p, cnt[4] = 1; 'c'
2. afce插入过程：
1）u = 0, s[0][0]前面得到过 = 1， p = 1.
2) u = 5, s[1][5] = 5, p = 5; 'f'
3) u = 2, s[5][2] = 6, p = 6, 'c'
4) u = 4, s[6][4] = 7, p = 7, cnt[7] = 1; 'e';
3. abc的插入过程：
1） u = 0, p = 0, s[0][0] = 1,
2) u = 1, s[1][1] = 2,
3) u = 2, s[2][2] = 3, cnt[3] = 1;
综上也就是在字符串集合当中有{abcd, afce, abc}; 分别代表的是cnt[4], cnt[7], cnt[3]各为1。
查找的时候类似，有的话就赋值，然后以新的起点这里继续往下寻找，for循环完查找结束之后，返回cnt[p]即是字符串的个数。
查找的代码如下：
int search(char str[])
int p = 0; for(int i = 0;str[i];i++) {int u = str[i] - 'a'; if(!s[p][u]) return 0; p = s[p][u]; } return cnt[p];
其实只要把s[p][u]理解成序号为p的字母往下延伸的某个字母u的编号即可以了，然后再将p指针不断的指向下面这个新位置。最后字符串插入或者循环结束，用上面只要出现过就加一次的cnt数组来计算字符串的出现次数。
完整的代码：
#include <cstdio> #include <iostream> using namespace std; const int N = 100010; int s[N][26], cnt[N], idx; int insert(char str[]) { int p = 0; for(int i = 0;str[i];i++) { int u = str[i] - 'a'; if(!s[p][u]) s[p][u] = ++idx; p = s[p][u]; } return cnt[p]++; } int search(char str[]) { int p = 0; for(int i =0;str[i];i++) { int u = str[i] - 'a'; if(!s[p][u]) return 0; p = s[p][u]; } return cnt[p]; } int main() { int n; cin>>n; char a,b[101]; while(n--){ cin>>a; if(a == 'I') { cin>>b; insert(b); } else if (a == 'Q') { cin>>b; cout<<search(b)<<endl; } } }
最大异或对：
#include <cstdio> #include <iostream> using namespace std; const int N = 100010, M = 31 * N; int n; int a[N], son[M][2], idx; void insert(int x) { int p = 0; for(int i = 30;i>=0;i--) { int t = x >> i & 1; if(!son[p][t]) son[p][t] = ++idx; p = son[p][t]; } } int search(int x) { int p = 0, res = 0; for(int i = 30;i>=0;i--) { int t = x >> i & 1; if(son[p][!t]) { p = son[p][!t]; res = res * 2 + !t; } else{ p = son[p][t]; res = res * 2 + t; } } return res; } int main() { cin>>n; for(int i = 0;i<n;i++) cin>>a[i]; int res = 0; for(int i = 0;i<n;i++) { insert(a[i]); int t = search(a[i]); res = max(res,a[i] ^ t); } cout<<res<<endl; }
假设我们要求3、4、5、6、7这5个数最大异或是多少？
数 字： 3 4 5 6 7
二 进 制：011 100 101 110 111
最大异或：0 7 6 5 4
程序运行的结果与我们手动推算一致：
5
3 4 5 6 7
3^3: 0
4^3: 7
5^3: 6
6^3: 5
7^3: 4
7
把这个过程抽象成trie树为：
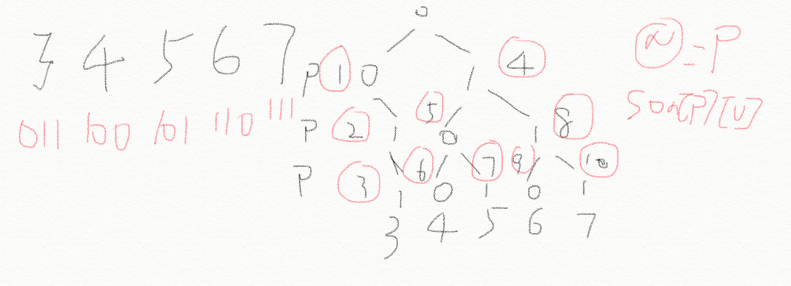
用红圈圈住的就是p的数字，即每个数转化成二进制0或1在trie树中的序号。每个son[p]数组有两种选择，往左是0，往右是1，所以M的大小是2*N = 2 * 10^5;
跟前面的建树过程一样，如果没有那么就新建，son[p][u] = ++idx, 代表用idx指针序号新建一个这样的编号，如果有的话，那么就不用建了，直接用p获取之前数组里面的内容：p = son[p][u]即可。3、4、5、6、7这5个数用2进制建的trie树即为如上图所示。
那么查找的过程一边插入，一边查找，就不是查找自己本身了，而是由高到低，找相反的那位即son[p][!u]有的话，就走这条，没有的话那就只能降而求其次选择已有的，
3（011）：一开始没有，自己与自己肯定是0，即3^3 = 0 ；
4（100）：从高到低，理想的情况是011，s[0][!1]是前面插入3存在的，s[1][1], s[2][1]都有，4 ^ 3 = 7;
5 (101) : 第一位最好是0, 所以是:5 ^ 3 = 110 = 6;
6(110) : 6 ^ 3 = 101 = 5;
7 (111): 7 ^ 3 = 100 = 4;
a[i]数组都是从0一直到最后求出每个数与前面的数最大的异或和，然后再把得到的这n个最大异或和再比较一次，就得到本题的答案了。
res = max(res, a[i] ^ t); cout<<res<<endl;
因为二进制每次都是*2的，所以res = res * 2 + t;来求得。
以上两种就是典型trie数的运用。
