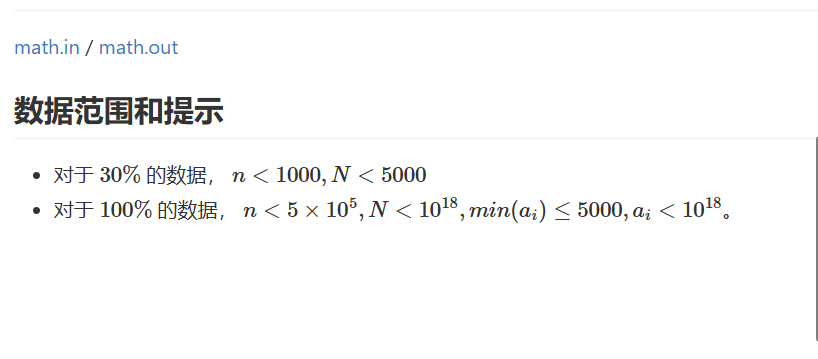【训练记录】2024年莆田市高中信息学奥赛国庆集训CSP-S提高组（第一天场外）

训练情况

rank#15

\(100 + 0 + 40 + 0 = 140\)

赛后反思

T3 忘记负数取模，丢了 \(60\) 分

T1. 跑步

显然，找到第一个大于 \(t\) 的 \(a,b,c\) 倍数，所以我们直接 \(t \div a,b,c\) 向上取整，再乘回去，最后减去 \(t\) 即可，注意一下 ceil 好像会爆

#include <bits/stdc++.h>
#define int long long

using namespace std;

void solve(){
    freopen("run.in","r",stdin);
    freopen("run.out","w",stdout);
	int a,b,c,t;
	cin>>a>>b>>c>>t;
	int aa = (t+(a-1))/a*a-t;
	int bb = (t+(b-1))/b*b-t;
	int cc = (t+(c-1))/c*c-t;
	cout<<min({aa,bb,cc})<<endl;
}

signed main(){
	// int T; cin>>T; while(T--)
	solve();
	return 0;
}

T2 邮件收发

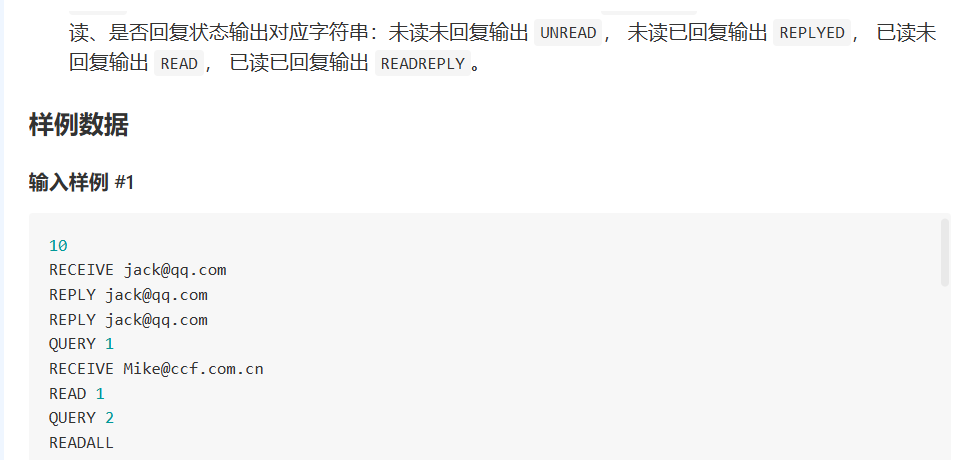
大模拟注意一下细节即可，对于 READALL 操作，我们可以采取记录当前的邮件数来判断，不必 \(O(n)\) 遍历，在下一次 QUERY 查询的时候比较一下邮件数即可。

#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;

int n;

map<string,bool> last;
map<string,int> lastcnt;
map<string,bool> laststate;
int readall;
int cnt;
map<int,int> mail;
map<string,string> from;

bool pd(string x){
	string username;
	string domain;
	for(int i = 0;i<x.size();i++){
		if(x[i] == '@'){
			username = x.substr(0,i);
			domain = x.substr(i+1);
			break;
		}
	}
	for(int i = 0;i<username.size();i++){
		if((username[i] >= 'a' && username[i] <= 'z') || (username[i] >= 'A' && username[i] <= 'Z') || (username[i] >= '0' && username[i] <= '9')) continue;
		return false;
	}
	if(username.size() < 3 || username.size() > 20) return false;



	for(int i = 0;i<domain.size();i++){
		if((domain[i] >= 'a' && domain[i] <= 'z') || domain[i] == '.') continue;
		return false;
	}
	if(domain[0] == '.' || domain[domain.size() - 1] == '.') return false;
	for(int i = 0;i<domain.size() - 1;i++){
		if(domain[i] == '.' && domain[i+1] == '.') return false;
	}
	if(domain.size() < 5 || domain.size() > 30) return false;

	return true;
}

void solve(){
	cin>>n;
	while(n--){
		string opt;
		cin>>opt;
		if(opt == "RECEIVE"){
			string email;
			cin>>email;
			if(!pd(email)){
				cout<<"ERR"<<endl;
				continue;
			}
			else {
				 cout<<"OK"<<endl;
				 last[email]=1;
				 lastcnt[email] = ++cnt;
				 laststate[email] = false;
				 mail[cnt] = 1; //1 未读 2已读未回复 3未读已回复 4已读已回复
			}
		} else if(opt == "REPLY"){
			string email;
			cin>>email;
			if(!pd(email)){
				cout<<"ERR"<<endl;
				continue;
			}
			if(!last[email]){
				cout<<"NOT FOUND"<<endl;
				continue;
			}
			if(laststate[email]){
				cout<<"REPLYED"<<endl;
				continue;
			}
			if(mail[lastcnt[email]] == 1) mail[lastcnt[email]] = 3;
			else if(mail[lastcnt[email]] == 2) mail[lastcnt[email]] = 4;
			else if(mail[lastcnt[email]] == 3) mail[lastcnt[email]] = 3;
			else if(mail[lastcnt[email]] == 4) mail[lastcnt[email]] = 4;
			cout<<"OK"<<endl;
			laststate[email] = 1;
		} else if(opt == "READ"){
			int x; cin>>x;
			if(!mail[x]) cout<<"NOT FOUND"<<endl;
			else {
				cout<<"OK"<<endl;
				if(mail[x] == 1) mail[x] = 2;
				else if(mail[x] == 2) mail[x] = 2;
				else if(mail[x] == 3) mail[x] = 4;
				else if(mail[x] == 4) mail[x] = 4;
			}
		} else if(opt == "READALL"){
			cout<<"OK"<<endl;
			readall = cnt;
		} else if(opt == "QUERY"){
			int x; cin>>x;
			if(cnt < x) cout<<"NOT FOUND"<<endl;
			else if(x <= readall){
				if(mail[x] >= 1 && mail[x] <= 2) cout<<"READ"<<endl;
				else if(mail[x] >= 3 && mail[x] <= 4) cout<<"READREPLY"<<endl;
			}
			else if(mail[x] == 1) cout<<"UNREAD"<<endl;
			else if(mail[x] == 2) cout<<"READ"<<endl;
			else if(mail[x] == 3) cout<<"REPLYED"<<endl;
			else if(mail[x] == 4) cout<<"READREPLY"<<endl;
		}
	}
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	// int T; cin>>T; while(T--)
	solve();
	return 0;
}

T3. 小果园

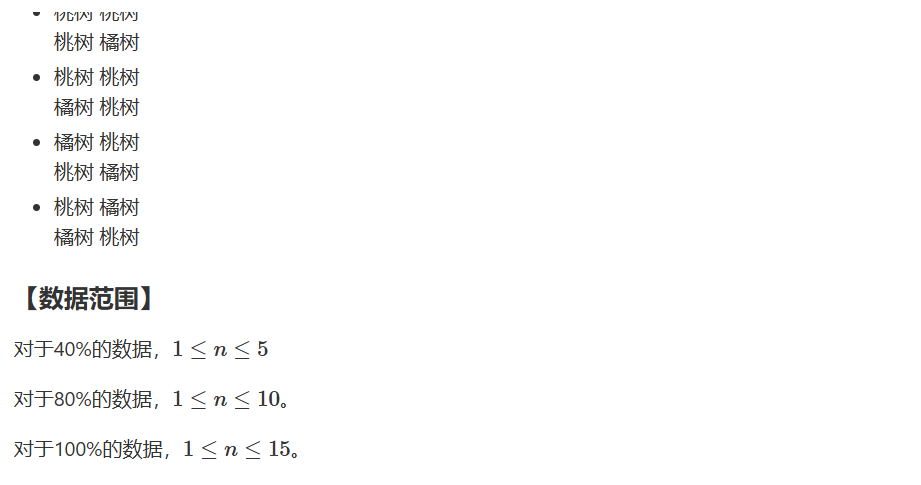
对于 \(40\%\) 的部分分，我们可以采用暴力 \(O(2^{n \times n})\) 枚举二维零一串，判断是否合法计数即可

对于 \(80\%\) 的部分分，我们可以使用状态压缩或者容斥定理（存疑）

公式推导晚点写，结论是

\[\sum_{k=0}^{n}\binom{n}{k}(-1)^k(2^{n-k}-1)^n \]

注意一下负数取模的问题

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int mod = 1e9 + 7;

int qpow(int a,int b){
	int x = a;
	int y = b;
	int ans = 1;
	while(y){
		if(y&1){
			ans *= x;
			ans %= mod;
		}
		x *= x;
		x %= mod;
		y >>= 1;
	}
	return ans%mod;
}

int inv(int x){
	return qpow(x,mod-2);
}

int combine(int n,int m){
	int fz = 1;
	for(int i = n;i>=n-m+1;i--) fz *= i,fz%=mod;
	int fm = 1;
	for(int i = 1;i<=m;i++) fm*=i,fm%=mod;
	return (fz*inv(fm))%mod;
}

void solve(){
    //freopen("xgy.in","r",stdin);
   // freopen("xgy.out","w",stdout);
	int n; cin>>n;
	int ans = 0;
	for(int k = 0;k<=n;k++){
		ans += (combine(n,k)*qpow(-1,k)*qpow(qpow(2,n-k) - 1,n)) % mod;
		ans %= mod;
	}
	cout<<(ans+mod)%mod<<endl;
}

signed main(){
	// int T; cin>>T; while(T--)
	solve();
	return 0;
}

T4. math