机器学习算法(3:决策树算法)
一、决策树简介
决策树是附加概率结果的一个树状的决策图,是直观的运用统计概率分析的图法。机器学习中决策树是一个预测模型,它表示对象属性和对象值之间的一种映射,一颗决策树是一棵有向无环树,它由若干个节点、分支、分裂谓词以及类别组成。树中的每一个节点表示对象属性的判断条件,其分支表示符合节点条件的对象。树的叶子节点表示对象所属的预测结果。
二、决策树的引导
下面是一段记者采访银行经理的对话(对话内容纯属虚构)
记者:向你们银行可以直接申请贷款要什么条件吗?
经理:只要年龄在30~50都可一申请到一定额度的贷款。
记者:那如果年龄超过50岁呢?
经理:那也没关系,只要办理我们银行的vip,也是可以申请贷款的。
记者:那如果年龄少于30岁的人该怎么办?
经理:那就看他是否有固定的收入。
记者:感谢与您的对话。
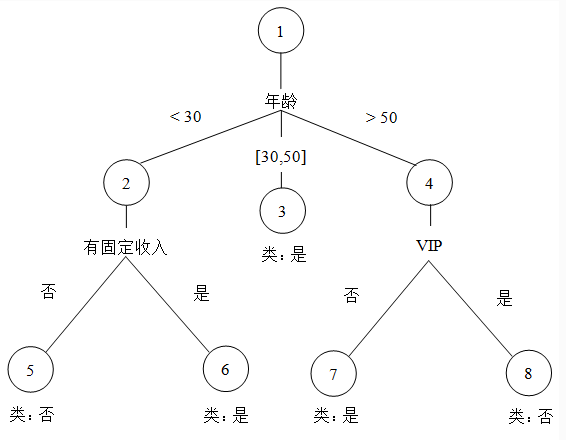
通过简单的对话我们构造了一个简单的决策树,如图所示,没有父亲节点的节点称为根节点,如图节点1。没有子节点的节点称为叶子节点,如图的3、5、6、7、8。一个节点按照某个属性分裂时,这个属性被称为分裂属性,如图中的年龄,有无固定收入和vip。同理每个分支都会被标记一个分裂谓词,这些分裂谓词就是分裂分节点的具体依据,例如图中的年龄就有对应三个分裂谓词“<30,[30,50],>50"每一个叶子节点都会被确定一个类标号,这里是”是“和”否“。
根节点:决策树的起源,进行分类的第一个特征属性,只有出边没有入边;
内部节点:进行分类的特征属性,有一条入边,至少有一条出边;
叶节点:分类结束的特征属性,有入边,没有出边;
三、决策树的构造
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。这里就要介绍一种判别属性优先分裂的方法---ID3算法
在ID3算法中,特征属性的选择是由目标函数决定的,目标函数代表的是特征属性的混乱程度(也就是特征属性越混乱越不好分类,该特征属性的分类顺序越靠后),这个目标函数就是信息增益,信息增益是由熵计算出来的,在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。具体细节看下面的介绍;
四、信息论基础
(1)熵:它度量了事物的不确定性,其值越大就越不确定,假如一个随机变量 的取值为
的取值为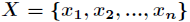 ,每一种取到的概率分别是
,每一种取到的概率分别是 ,那么
,那么 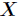 的熵定义为
的熵定义为
 的取值为
的取值为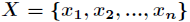 ,每一种取到的概率分别是
,每一种取到的概率分别是 ,那么
,那么 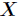 的熵定义为
的熵定义为 意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。(2)条件熵:条件熵的表达式H(X|Y),它度量了我们的X在知道Y以后剩下的不确定性,其表达式如下
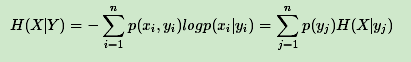
(3)信息增益:信息增益是特征选择中的一个重要指标,它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要,其值为H(X) - H(X|Y)。
总结:在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略,以上 就是ID3算法的核心思想。
五、python代码实现说明
- 在给定的数据中,我们先选出信息增益最大的那个属性来作为根节点;
- 若样本都在同一类,则为叶子点;
- 将以作为节点的数据删除,再次寻找信息增益最大的那个属性进行分裂,不断递归;
- 递归结束标记为如下:
- 所有属性都用完,若所用属性都用完后还未分类完,则依照少数服从多数来看;
- 某一属性的分类结果都一致;
六、python代码实现
from math import log
import operator
dataSet = [[1,1,0,'fight'],[1,0,1,'fight'],[1,0,1,'fight'],
[1,0,1,'fight'],[0,0,1,'run'],[0,1,0,'fight'],
[0,1,1,'run']] #需处理的数据
labels = ['weapon','bullet','blood'] #对应的标签
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
lableCounts = {}
for featVec in dataSet:
currentLable = featVec[-1] #取数据中各元素的最后一项:类别
if currentLable not in lableCounts.keys():
lableCounts[currentLable] = 0
lableCounts[currentLable] += 1 #给类别计数
shannonEnt = 0
for key in lableCounts:
prob = float(lableCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #计算熵的值
return shannonEnt #返回熵的值
def splitDataSet(dataSet,axis,value):
retDataSet = [] #创建新列表retDataSet
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #减去最后一项(类别)
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value) #调用splitDataSet函数
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet) #计算条件熵的值
infoGain = baseEntropy -newEntropy #计算信息增益的值
if infoGain > bestInfoGain:
bestInfoGain = infoGain
bestFeature = i #比较信息增益
return bestFeature #返回信息增益最大的位置
'''因为我们递归构建决策树是根据属性的消耗进行计算的,所以可能会存在最后属性用完了,
但是分类还是没有算完,这时候就会采用多数表决的方式计算节点分类'''
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
return max(classCount) #返回多数表决后的结果
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) ==len(classList):
return classList[0] #所有类别都相同则停止划分,直接返回该类别
if len(dataSet[0]) == 1: #所有特征已经用完
return majorityCnt(classList) #返回多数表决后的结果
bestFeat = chooseBestFeatureToSplit(dataSet) #调用chooseBestFeatureToSplit函数
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat]) #删除信息增益最大的位置对应的标签
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:] #为了不改变原始列表的内容复制了一下
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
myTree = createTree(dataSet,labels)
print myTree
{'weapon': {0: {'blood': {0: 'fight', 1: 'run'}}, 1: 'fight'}}
七、ID3算法的缺点
- ID3算法往往偏向于选择取值较多的属性,而在很多情况下取值较多的属性并不总是最重要的属性;
- ID3算法不能处理具有连续值的属性,也不能处理具有缺失数据的属性;
- ID3算法虽然理论清晰,但计算比较复杂,在学习和训练数据集的过程中机器内存占用率比较大,耗费资源;
- 在建造决策树时,每个结点仅含一个属性,是一种单变元的算法,致使生成的决策树结点之间的相关性不够强,虽然在一棵树上连在一起,但联系还是松散的;




