BZOJ2180: 最小直径生成树
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2180
2180: 最小直径生成树
Time Limit: 10 Sec Memory Limit: 259 MBSubmit: 195 Solved: 93
[Submit][Status][Discuss]
Description
Input
Output
Sample Input
1 2 0
2 3 1
3 1 2
Sample Output
[数据范围]
0 < M < = 1000
0 < = Z < = 1000
HINT
Source
最小直径生成树。。。话说网上讲这个的好像不是很多。。。反正我只找到一篇(http://blog.csdn.net/crazy_ac/article/details/8816877)。。。
为了防止以后忘了怎么写,还是来写一波吧。。
最小直径生成树,顾名思义,就是直径最小的生成树(手动滑稽)(不知道树的直径是什么的童鞋,请出门左转,自行百度)。。
这里再介绍一个概念,树的绝对中心,就是树上到各点距离最大值最小的点,这个绝对中心可以在边上。
很显然,绝对中心到其他点的距离最大值会出现两次。最小直径生成树的直径就是绝对中心到其他点的距离最大值*2。那么我们只要求出绝对中心,这题就解决了。
由于绝对中心可能在边上,我们需要枚举每条边,来找绝对中心。
假设我们枚举的边为(u,v),边的长度为L。那么这条边上的点到点S的距离函数f(x)的图像应该为下图:
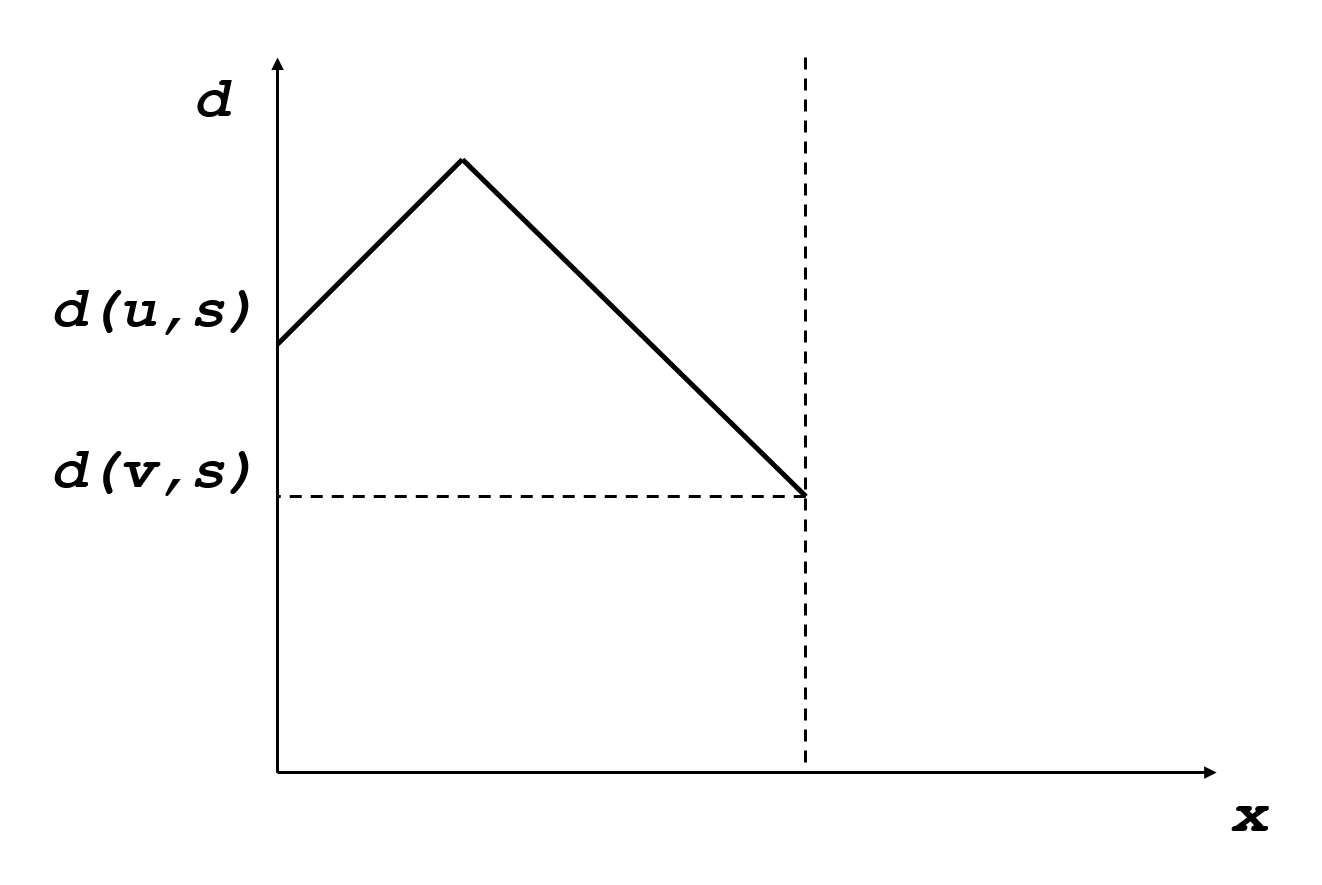
整个图有n个点,那么我们需要画出n条这样的折线,绝对中心必定在是最上面那一部分折线中最低的那个,如下图。

(好吧我承认这图是从我前面说的那篇博客复制的。。)
但如果是n条毫无规律的折线,要用程序找出最低的那个点有点困难,我们需要进一步挖掘。
我们发现如果d(x,u)>d(y,u)&&d(x,v)>d(y,v),那么y点毫无卵用,因为代表y的折线必定在x下方,如下图。
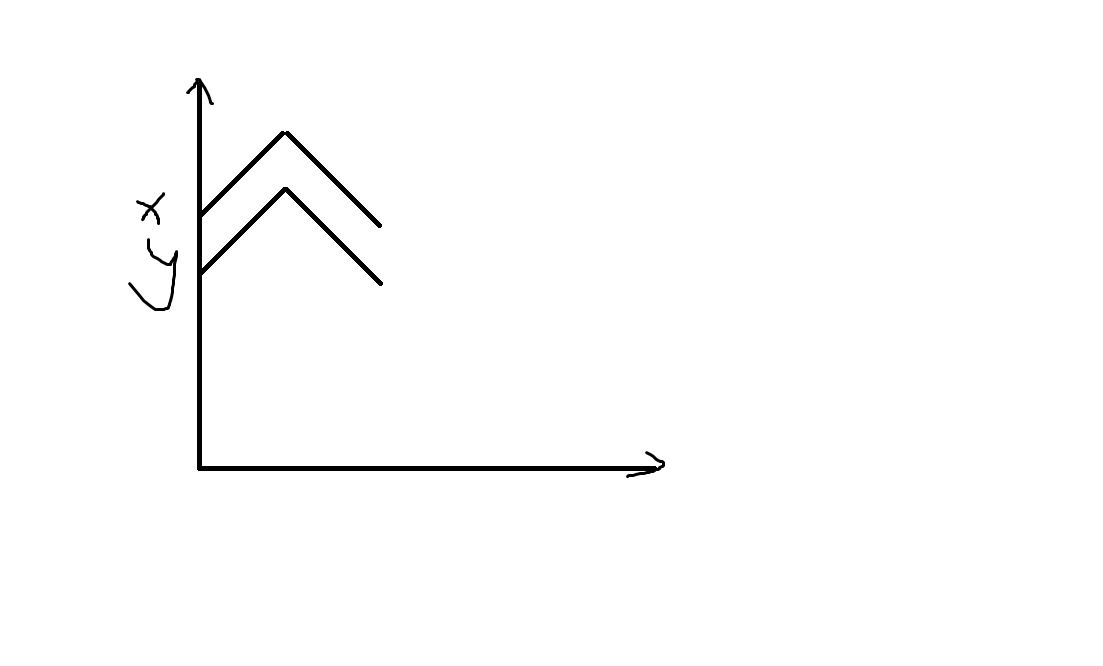
当我们把所有没用的点都删掉,并把留下来的点按到u的距离升序排序后,便会发现他们有一些优美的性质:它们到v的距离是严格递减的。
那么这下就好办了,因为最上面的部分的转折点一定是排序后两个相邻的点的折线的交点,那么我们排序后扫一遍就好了。
(啥?你不会写?看代码吧。。)
#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 1005
using namespace std;
int n,m,ans,dist[maxn][maxn],rank[maxn][maxn];
int read(){
int x=0,f=1;char ch;
for(ch=getchar();ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
return x*f;
}
int main(){
n=read();m=read();memset(dist,63,sizeof(dist));
for(int i=1;i<=n;i++)dist[i][i]=0;
for(int i=1,x,y,z;i<=m;i++){
x=read();y=read();z=read();
dist[x][y]=dist[y][x]=min(dist[x][y],z);
}
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)rank[i][j]=j;
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)if(k!=i)
for(int j=1;j<=n;j++)if(i!=j&&k!=j)
dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=j+1;k<=n;k++)
if(dist[i][rank[i][j]]<dist[i][rank[i][k]])swap(rank[i][j],rank[i][k]);
ans=1e9;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)if(i!=j){
ans=min(ans,dist[i][rank[i][1]]+dist[i][rank[i][2]]);
ans=min(ans,dist[j][rank[j][1]]+dist[j][rank[j][2]]);
for(int b=1,a=2;a<=n;a++)
if(dist[j][rank[i][b]]<dist[j][rank[i][a]])
ans=min(ans,dist[j][rank[i][b]]+dist[i][rank[i][a]]+dist[i][j]),b=a;
}
printf("%d\n",ans);
return 0;
}
(你说我代码太丑了?好吧,我承认。。。)
(话说为什么博客园推荐的代码插入器显示出来后丑死了,没有推荐的那个好看多了。。。)

