解题报告 smoj 2019初二创新班(2019.4.21)
解题报告 smoj 2019初二创新班(2019.4.21)
时间:2019.4.25
T1:删除
题目描述
给你\(N, N \le 2 \times 10^9\)个元素的数组(下标从\(1\)开始),一开始数组里的数是\(\{1,2,3,…,N\}\),然后执行\(D\)次删除操作。每次删除操作给一个区间\([l, r]\),要求删除下标位置从\(l\)到\(r\)的数,此时数组里的数据个数会减少\((r - l +1)\)个。
例如,\(N=8\),一开始数组里的数是\(\{1, 2, 3, 4, 5, 6, 7, 8\}\)。第\(1\)次删除操作区间是\([3, 4]\),结果为\(\{1,2,5,6,7,8\}\); 第\(2\)次删除操作区间是\([4, 5]\),结果为\(\{1, 2, 5, 8\}\)。
最后,输出第\(M\)位的数字是什么。如果剩余的数不够\(M\)个,输出\(-1\)。
\(N\)范围为\([1, 2000000000]\),\(M\)范围为\([1, N]\),\(D\)范围为\([1, 50]\)。
分析
观察到\(N\)很大,而且只有删除操作。
不妨将删除排序。可以发现删除的区间要么嵌套,要么不相交。如下图,删除B的左端点不可能在A的范围中,右端点也同理。
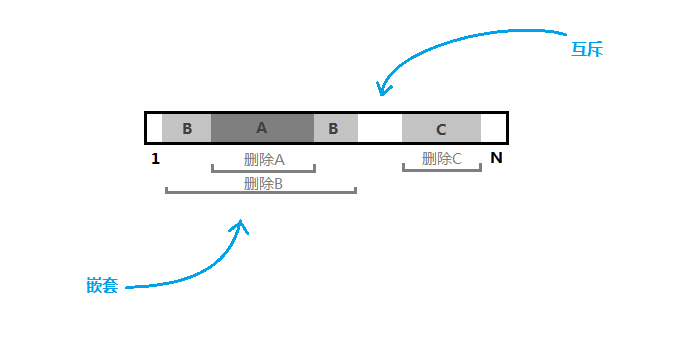
只要求出各个删除区间对应原序列在\([1, N]\)之间的位置,并将被包含的无用区间(如图中A)删除,即可求出\(M\)的位置。
代码
实现上,使用vector存储所有的区间。每添加一次删除,先计算出该删除的左右端点对应原序列的位置,然后将vector里它所包含的区间删除,将它添加进vector里,最后对vector排序。
时间复杂度:\(O(D^2 \log D), D \le 50\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int kMaxN = 50 + 10;
const int kInf = 2000000000 + 1000;
void Read(const char* str, int len, int& l, int& r) {
l = r = 0;
for (int i = 0; i < len; i++) {
if (str[i] == '-') {
swap(l, r);
} else {
r = r * 10 + str[i] - '0';
}
}
// printf(">>> str = %s, [l, r] = [%lld, %lld]\n", str, l, r);
}
struct Range {
int l, r;
};
bool Comp(const Range& x, const Range& y) {
return x.r < y.r;
}
// 保证sort by `r`
// 保证不相交
vector<Range> range;
int GetRealPos(int x) {
for (int i = 0; i < range.size(); i++) {
const Range& ran = range[i];
if (ran.l <= x) {
x += ran.r - ran.l + 1;
}
}
return x;
}
void AddRange(int l, int r) {
for (int i = 0; i < range.size(); i++) {
Range& ran = range[i];
if (ran.r < l || r < ran.l) {
continue;
} else {
assert(l <= ran.l && ran.r <= r);
ran.r = kInf;
}
}
sort(range.begin(), range.end(), Comp);
int new_size = range.size();
for (int i = 0; i < range.size(); i++) {
if (range[i].r == kInf) {
new_size = i;
break;
}
}
range.resize(new_size);
range.push_back((Range) {l, r});
sort(range.begin(), range.end(), Comp);
}
int T;
int n, k, m;
int l, r;
char buffer[127];
signed main() {
freopen("2878.in", "r", stdin);
freopen("2878.out", "w", stdout);
scanf("%lld", &T);
while (T--) {
range.clear();
scanf("%lld %lld %lld", &n, &k, &m);
for (int i = 1; i <= m; i++) {
scanf("%s", buffer);
Read(buffer, strlen(buffer), l, r);
l = GetRealPos(l);
r = GetRealPos(r);
AddRange(l, r);
}
int ans = GetRealPos(k);
if (ans > n) {
printf("-1\n");
} else {
printf("%lld\n", ans);
}
}
return 0;
}
T2:巡回
题目描述
某个国家有\(N\)个城市,编号为\(0\)到\(N-1\)。\(M\)条双向马路,每条路连接\(2\)个城市。奶牛\(Shary\)喜欢在路上巡回,不喜欢停留在城市里,总是从一个城市到另一个城市。\(Shary\)走第\(i\)条路花费的时间是\(Ci\)(两个方向花费时间相同)。
现在\(Shary\)开始在\(0\)号城市,她希望恰好花费\(T\)时间,巡回到达\(N-1\)号城市。请你编程判断是否存在这个方案,如果存在输出"Possible";否则输出"Impossible"。
数据范围:\(N\)和\(M\)不超过\(50\),\(T\)不超过\(10^{18}\)。\(Ci\)的范围是\([1,10000]\)
分析
为了方便,下文均用\(s\)来表示\(\it 0\)号节点,用\(\it t\)来表示\(\it {N - 1}\)号节点。
让我们看一看下面这张图:

从\(s\)出发,我们经过许多路径后到达了\(t\),然后找到一个与\(t\)相连的节点\(v\),并在相连的边\((t, v)\)上连续跳跃偶数次(当然也可以为\(0\)次),直到凑出\(T\)为止。
我们发现,这种情况是一定会发生的,而且从\(s\)出发经过的所有路径中,除了这条边\((t, v)\)外,没有一条边经过的次数会大于\(20000\)次。
这是因为每条边的权值不超过\(10000\),所以,若在别的边上跳跃了\(cnt (cnt > 20000)\)次,就可以转化为多在\((t, v)\)上跳跃\(\left \lfloor \dfrac {cnt} {2 \times d}\right \rfloor\)次,而只在这条边上跳跃\(cnt \mod (2 \times d)\)次,不影响答案。
枚举每一个与\(t\)相连的\(v\),得到\((t, v)\)的权值\(d\),然后判断能否从\(s\)到\(t\)走出一条与\(T\)在模\(2 \times d\)意义下同余的路径即可(想一想,为什么)。
同余最短路
考虑\(SPFA\)。记录一个全局的模数\(K\),用\(dis[u][x]\)表示到达\(u\)时,经过的路程\(\mod K\)刚好为\(x\)时的最短路。
松弛与普通\(SPFA\)类似,若\(y = x + dis\),\(dis[v][y] = \min(dis[u][x] + dis)\)。
同余最短路的本质其实是拆点。可以理解为将\(u\)拆成\(K\)个点,分别为\(u_0, u_1 ... u_{K - 1}\)。其中\(u_x\)就表示从起点到\(u\)时,路程与\(x\)在模\(K\)下同余的状态。

如图,在两排的点中间连边。实现代码上,我们并不需要将这\(K\)条边全部建出,直接对着数组松弛即可。
本题中,枚举每一个\(v\),令\(K = 2 \times d\),跑同余最短路即可。时间复杂度:\(O(N \times C \times k)\),这里的\(k\)是\(SPFA\)里的未知数。
代码
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int kMaxN = 50 + 10;
const int kMaxM = 50 + 10;
const int kMaxMod = 20000 + 10;
const LL kInf = 2e18;
struct Graph {
struct Arc {
int to, dis;
};
vector<Arc> arcs[kMaxN];
void Clear(int n) {
for (int i = 1; i <= n; i++) arcs[i].clear();
}
void Add(int u, int v, int dis) {
arcs[u].push_back((Arc) {v, dis});
arcs[v].push_back((Arc) {u, dis});
}
};
struct Node {
int u, x;
};
int T;
Graph G;
int n, m, s, t;
LL target;
LL dis[kMaxN][kMaxMod];
bool in[kMaxN][kMaxMod];
queue<Node> Q;
void Spfa(int mod) {
for (int i = 1; i <= n; i++) {
for (int j = 0; j < mod; j++) {
dis[i][j] = kInf;
}
}
dis[s][0] = 0;
Q.push((Node) {s, 0});
while (!Q.empty()) {
Node node = Q.front();
Q.pop();
int u = node.u;
int x = node.x;
in[u][x] = false;
for (int i = 0; i < G.arcs[u].size(); i++) {
Graph::Arc& arc = G.arcs[u][i];
int v = arc.to;
int d = arc.dis;
int y = (x + d) % mod;
if (dis[u][x] + d < dis[v][y]) {
dis[v][y] = dis[u][x] + d;
if (!in[v][y]) {
in[v][y] = true;
Q.push((Node) {v, y});
}
}
}
}
}
int main() {
freopen("2879.in", "r", stdin);
freopen("2879.out", "w", stdout);
scanf("%d", &T);
while (T--) {
scanf("%d %d %lld", &n, &m, &target);
G.Clear(n);
s = 1;
t = n;
for (int i = 1; i <= m; i++) {
int u, v, dis;
scanf("%d %d %d", &u, &v, &dis);
G.Add(u + 1, v + 1, dis);
}
bool flag = false;
for (int i = 0; i < G.arcs[t].size(); i++) {
Graph::Arc& arc = G.arcs[t][i];
int d = arc.dis << 1;
Spfa(d);
if (dis[t][target % d] <= target) {
flag = true;
break;
}
}
if (flag) {
printf("Possible\n");
} else {
printf("Impossible\n");
}
}
return 0;
}
T3:糖果
题目描述
你和朋友\(Shary\)玩一个游戏:在一个无环的、无向的图中,每个节点可以放一些糖果。每次\(Shary\)可以从糖果数不少于\(2\)的节点上拿\(2\)个糖果,吃掉\(1\)个,并把另一个糖果放到相邻的某个节点去。如果在某个时候,目标节点\(T\)上有了糖果,游戏结束,\(Shary\)赢。
如果你设计的初始状态,无论如何\(Shary\)都赢不了,则\(Shary\)输。
给定一个图,你能赢的方案中可以放的最多糖果数是多少?如果答案数超过\(2\times10^9\),只要输出\(-1\)即可。
分析
题目中的移动即为下图所示。

首先,判断原图是否连通。若不连通,你就可以在\(T\)所在连通分量之外的地方放任意多颗糖果,输出\(-1\)。
若图连通,那么图就成了一棵树。不妨令目标\(T\)为原树的根。可以发现,\(Shary\)的策略是尽量将所有节点的糖果都往根的方向移动。
怎么放尽量多的糖果,使\(Shary\)无法将任意一颗糖果送到根去呢?考虑一种特殊的情况:原树是一条链,其中\(T\)是链的一个端点。
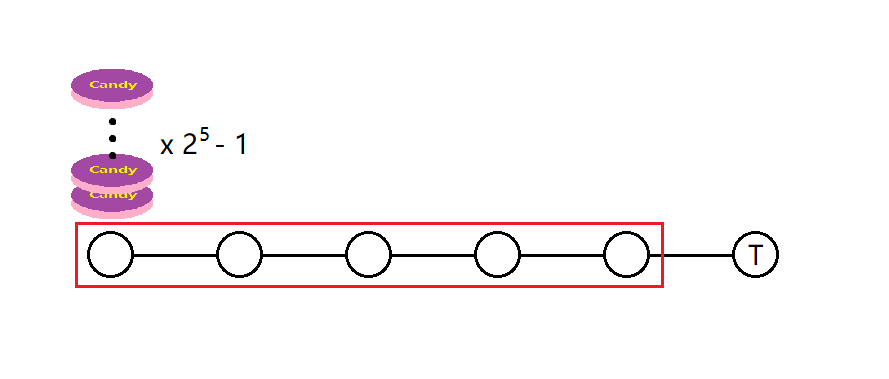
我们发现,在这条链的另一个端点放置\(2 ^ \text{红框的长度} - 1\)颗糖果是最优的。可以这样考虑:一开始在红框的右端放置一颗糖果,然后不停地向左移动,每次移动后将大小\(\times 2 + 1\)。

可以发现这样能让我们放置糖果的数量尽量多,而且保证\(Shary\)无法将糖果移动到\(T\)去。最后在这条链的端点处刚好有\(2 ^ {len} - 1\)颗糖果。
接下来,考虑把问题转回到树上。很容易联想到长链剖分(树链剖分的一种,每个节点保存一个len,表示到达子树中叶子节点的距离最大值,并通过len确定“重儿子”)。长链剖分能够保证剖分出的每一条树链长度最长。
长链剖分后,把每一条长链当成是上图中的“红框”就行了。若这条长链的长度是\(len\),那么答案加上\(2 ^ {len} - 1\)。可以发现这种策略一定能够达到最优。
若长链的一端是根,记得不要把根算进去(见代码输出前的那个for)
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int kMaxN = 50 + 10;
const LL kInf = 2000000000;
struct Graph {
vector<int> lis[kMaxN];
void Clear(int n) {
for (int i = 1; i <= n; i++) lis[i].clear();
}
void Add(int u, int v) {
lis[u].push_back(v);
}
};
int T;
Graph G;
int n, root;
char buffer[kMaxN];
void ReadGraph() {
G.Clear(n);
for (int i = 0; i < n; i++) {
scanf("%s", buffer);
for (int j = 0; j < n; j++) {
if (buffer[j] == 'Y') {
G.Add(i + 1, j + 1);
}
}
}
}
int len[kMaxN], wson[kMaxN];
void Dfs1(int u, int fa) {
len[u] = 1;
wson[u] = 0;
for (int i = 0; i < G.lis[u].size(); i++) {
int v = G.lis[u][i];
if (v != fa) {
Dfs1(v, u);
if (len[v] + 1 > len[u]) {
len[u] = len[v] + 1;
wson[u] = v;
}
}
}
}
int top[kMaxN];
void Dfs2(int u, int fa) {
if (wson[u]) {
top[wson[u]] = top[u];
Dfs2(wson[u], u);
}
for (int i = 0; i < G.lis[u].size(); i++) {
int v = G.lis[u][i];
if (v != fa && v != wson[u]) {
top[v] = v;
Dfs2(v, u);
}
}
}
int main() {
freopen("2880.in", "r", stdin);
freopen("2880.out", "w", stdout);
scanf("%d", &T);
while (T--) {
memset(len, 0, sizeof(len));
bool is_connected = true;
scanf("%d %d", &n, &root);
root++;
ReadGraph();
Dfs1(root, 0);
for (int i = 1; i <= n; i++) {
if (!len[i]) {
is_connected = false;
break;
}
}
if (!is_connected) {
printf("-1\n");
continue;
}
top[root] = root;
Dfs2(root, 0);
LL ans = 0;
for (int i = 1; i <= n; i++) {
if (top[i] == i && i != root) {
ans += (1ll << len[i]) - 1;
if (ans > kInf) break;
} else if (i == root) {
ans += (1ll << (len[i] - 1)) - 1;
if (ans > kInf) break;
}
}
if (ans > kInf) {
printf("-1\n");
} else {
printf("%lld\n", ans);
}
}
return 0;
}


