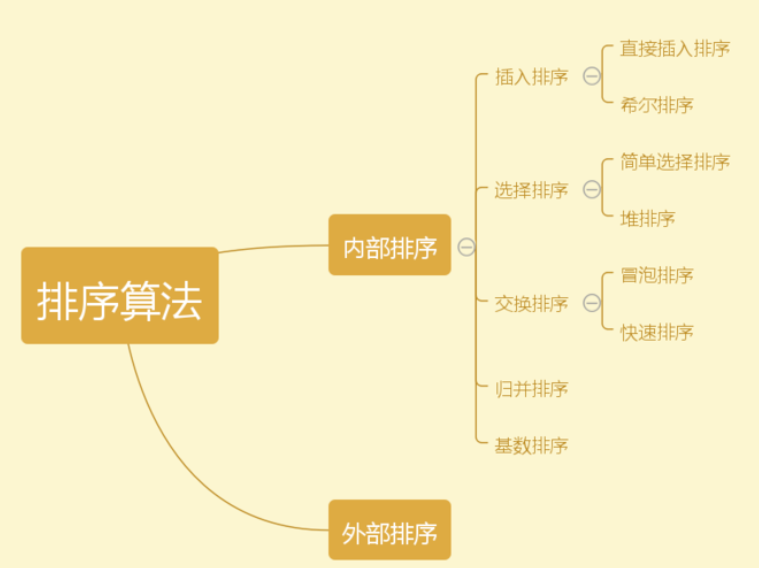
八大排序算法
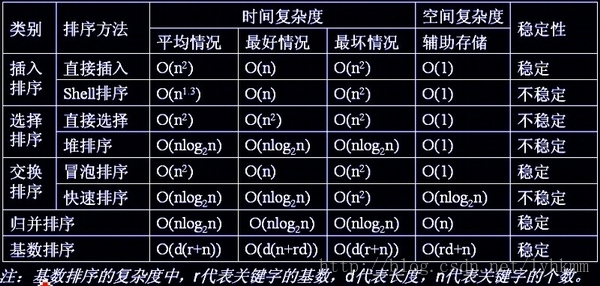
关系和复杂度
关系
复杂度
一、冒泡排序
原理
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
代码
void bubble_sort(int a[], int size){
for(int i = 0; i < size-1; ++i){
for(int j = 0; j < size-1-i; ++j){
if( a[j] > a[j+1] ){
swap(a, j, j+1);
}
}
}
}
二、选择排序
原理
选择排序与冒泡排序有点像,只不过选择排序每次都是在确定了最小数的下标之后再进行交换,大大减少了交换的次数
代码
void select_sort(int a[], int size){
for(int i = 0; i < size-1; ++i){
int minIndex = i;
for(int j = i; j < size; ++j){
if(a[j] < a[minIndex]) minIndex = j;
}
if( minIndex != i){
int temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
}
三、插入排序
原理
将一个记录插入到已排序的有序表中,从而得到一个新的,记录数增1的有序表
代码
void insert_sort(int a[], int size){
for(int i = 1; i < size-1; ++i){
int key = a[i];
int j = i-1;
while( j >= 0 && a[j] > key ) {
a[j+1] = a[j];
j--;
}
a[j+1] = key;
}
}
四、快速排序
原理
通过一趟排序将序列分成左右两部分,其中左半部分的的值均比右半部分的值小,
然后再分别对左右部分的记录进行排序,直到整个序列有序。
代码
int partition(int a[], int low, int high){
int key = a[low];
while( low < high ){
while(low < high && a[high] >= key) high--;
a[low] = a[high];
while(low < high && a[low] <= key) low++;
a[high] = a[low];
}
a[low] = key;
return low;
}
void quick_sort(int a[], int low, int high){
if(low >= high) return;
int keypos = partition(a, low, high);
quick_sort(a, low, keypos-1);
quick_sort(a, keypos+1, high);
}
五、堆排序
原理
假设序列有n个元素,先将这n建成大顶堆,然后取堆顶元素,与序列第n个元素交换,然后调整前n-1元素,使其重新成为堆,然后再取堆顶元素,与第n-1个元素交换,再调整前n-2个元素...直至整个序列有序。
代码
//当列表第一个是以下标0开始,结点下标为i,左孩子则为2*i+1,右孩子下标则为2*i+2,若下标以1开始,左孩子则为2*i,右孩子则为2*i+1
void heapAdjust(int a[], int s, int m){
int key = a[s];
for(int j = 2*s + 1; j <= m; j = 2*j + 1 ){
if(j < m && a[j] <= a[j+1] ) ++j;
if( a[j] <= key ) break;
a[s] = a[j];
s = j;
}
a[s] = key;
}
void heap_sort(int a[], int size){
//初始建堆,从最后一个非叶子节点开始
for(int i = size/2-1; i >= 0; --i){
heapAdjust(a, i, size-1);
}
//取堆顶,并且调整
for(int i = size-1; i > 0 ; --i){
swap(a, 0, i);
heapAdjust(a, 0, i-1);
}
}
六、希尔排序
原理
希尔排序是插入排序的一种高效率的实现,也叫缩小增量排序。简单的插入排序中,如果待排序列是正序时,时间复杂度是O(n),如果序列是基本有序的,使用直接插入排序效率就非常高。希尔排序就利用了这个特点。基本思想是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时再对全体记录进行一次直接插入排序。
代码
void shell_insert(int a[], int size, int d){
for(int i = d; i < size; i++){
int j = i - d;
int key = a[i];
while( j >= 0 && a[j] > temp){
a[j+d] = a[j];
j -= d;
}
if(j != i-d)
a[j+d] = key;
}
}
void shell_sort(int a[], int size){
int d = size/2;
while(d >= 1){
shell_insert(a, size, d);
d /= 2;
}
}
七、归并排序
原理
- 把有序表划分成元素个数尽量相等的两半
- 把两半元素分别排序
- 把两个有序表合并成一个
代码
void merge(int a[], int first, int mid, int last){
int temp[last-first+1];
int copyIndex = last - first;
int i = mid, j = last;
while( i>=first && j >= mid+1 ){
if(a[i] > a[j]) temp[copyIndex--] = a[i--];
else temp[copyIndex--] = a[j--];
}
while(i >= first ) temp[copyIndex--] = a[i--];
while(j >= mid+1) temp[copyIndex--] = a[j--];
for(int k = first; k <= last; ++k){
a[k] = temp[k-first];
}
}
void merge_sort(int a[], int first, int last){
if( first >= last) return;
int mid = (first + last)/2;
merge_sort(a, first, mid);
merge_sort(a, mid+1, last);
merge(a, first, mid, last);
}
八、计数排序
原理
当待排序的数的值都是在一定的范围内的整数时,可以用待排序的数作为计数数组的下标,统计每个数的个数,然后依次输出即可。
代码
void count_sort(int a[], int size){
int mx = a[0];
for(int i = 1; i < size; ++i)
mx = a[i] > mx ? a[i] :mx;
int* count = new int[mx+1](); //有() 默认初值为0
for(int i = 0; i < size; ++i)
count[a[i]] ++;
int id = 0;
for(int i = 0; i <= mx; ++i){
for(int j = 0; j < count[i]; ++j)
a[id++] = i;
}
delete[] count;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号