路径分析算法—基于Dijkstra算法的路径分析
原文链接：路径分析算法—基于Dijkstra算法的路径分析 – 每天进步一点点
路径分析是算法领域最为基础的算法分析之一，它包含了最短路径算法、路径规划算法等。无论是单源的最短路径或者多源的最短路径，以及基于概率路径等，在目前的日常应用中均会涉及，它们成为解决概率图问题、路径规划问题的有效解决方法。
Dijkstra（迪杰斯特拉）算法是典型的最短路径路由算法，也是一种单源路径算法，用于计算一个节点到其他所有节点的最短路径。该算法的主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止，Dijkstra算法对于处理非负权边的最短路径问题是比较高效的。Dijkstra 算法方法简明，能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低，同时在运算时占用空间大。
1.例子
在某个极地探险活动中，主办方给出了如下表所示的路径关系图，从入口到出口会经过丘陵、沼泽、河流、草地等，它们之间也可以相互到达，路径距离以“小时”为单位，如从沼泽到草地需要4小时完成，谁能够最早从入口到达出口，就被评为“极地先锋”。
| 入口 | 丘陵 | 沼泽 | 河流 | 草地 | 出口 | |
| 入口 | – | 6 | 3 | – | – | – |
| 丘陵 | 6 | – | 2 | 5 | – | – |
| 沼泽 | 3 | 2 | – | 3 | 4 | – |
| 河流 | – | 5 | 3 | – | 2 | – |
| 草地 | – | – | 4 | 2 | – | 3 |
| 出口 | – | – | – | 3 | 5 | 5 |
2.基于Dijkstra的最短路径规划
Dijkstra 算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容并有详细的介绍，如数据结构、图论、运筹学等。其基本思想是，设置顶点集合S并不断地进行贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时，S中仅含有源。设U是G的某一个顶点，把从源到U且中间只经过S中顶点的路称为从源到U的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra 算法每次从V-S中取出具有最短特殊路长度的顶点U，将U添加到S中，同时对数组dist进行必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其他顶点之间的最短路径长度。
根据极上面地探险的活动表，画出下图的无向图，计算出从入口到出口的耗时最短路径。
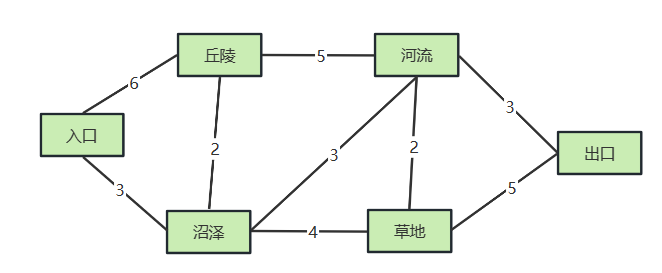
我们约定同一个地点之间的距离为，不可以直接到达的两点之间的距离为无穷大。那么从入口开始，寻找最短路径的步骤如下表：
| 步骤 | S集合 | U集合 |
| 1 | 选“入口”，初始化S={“入口”} 最短路径： Dist{“入口”，“入口”}=0 以“入口”为起点，向下寻找邻接地理位置 |
初始化U={“丘陵”,“沼泽”，“河流”，“草地”，“出口”} 计算： Dist{“入口”,“丘陵”}=5， Dist{“入口”,“沼泽”}=3， Dist{“入口”,“河流”}=Dist{“入口”,“草地”}=Dist{“入口”,“出口”}=无穷大 |
| 2 | 选“沼泽”,S={“入口”，“沼泽”} 最短路径Min=Dist{“入口”,“沼泽”}=4 此时以“沼泽”作为新的起点，向临近点继续寻找 |
U={“丘陵”,”河流”,”草地”,”出口”} 计算： Dist{“入口”,”沼泽”，“丘陵”}=5， Dist{“入口”,”沼泽”，“河流”}=6， Dist{“入口”,”沼泽”，“草地”}=7， Dist{“入口”,”沼泽”，“出口”}=无穷大， |
| 3 | 选”丘陵“，S={“入口”,”沼泽”,”丘陵”} 由于 Dist{“入口”，“入口”}=0 Dist{“入口”，“沼泽”}=3 Min=Dist{“入口”,”沼泽”,”丘陵”}=5 因此，最短路径依次为”入口“，”沼泽“，”丘陵“ 让”丘陵“作为中间位置，继续向邻近位置寻找。 |
U={“河流”,”草地”,”出口”} 计算： Dist{“入口”,”沼泽”,”丘陵”,”河流”}=10 Dist{“入口”,”沼泽”,”河流”}=6 |
| 4 | 选”河流”，S={“入口”，”沼泽”，”丘陵”,”河流”}，此刻为最短路径 Dist{“入口”，“入口”}=0 Dist{“入口”，“沼泽”}=3 Dist{“入口”，“沼泽”，”丘陵”}=5 Min=Dist{“入口”，“沼泽”，”河流”}=6 以“河流”为中间点，从“入口”、“沼泽”开始寻找路径 |
U={“草地”,”出口”} 计算： Dist{“入口”,”沼泽”,”河流”,”草地”}=8 Dist{“入口”,”沼泽”,”草地”}=7 Dist{“入口”,”沼泽”,”河流”,”出口”}=9 |
| 5 | 选“草地”,S={“入口”,”沼泽”,”丘陵”,”河流”,”草地”} 此时最短路径： Dist{“入口”，“入口”}=0 Dist{“入口”，“沼泽”}=3 Dist{“入口”，”沼泽”,”丘陵”}=5 Dist{“入口”，”沼泽”,”河流”}=6 Min=Dist{“入口”,”沼泽”,”草地”}=7 以”草地”为中间点，从”入口”,”沼泽”，”草地”继续开始寻找 |
U={“草地”} Dist={“入口”,”沼泽”,”草地”,”出口”}=12 Dist={“入口”,”沼泽”,”河流”,”出口”}=9 发现“入口”，“沼泽”，“河流”，“出口”路径最短 |
| 6 | 选“出口”，S={“入口”,”沼泽”，”丘陵”,”河流”，”草地 “，”出口”} Min=Dist{“入口”，”沼泽”,”河流”,”出口”}=9 |
U={},路径寻找结束 |
通过上述路径寻找过程可以发现，当“极地探险”的路径为“入口”、“沼泽”、“河流”、“出口”时，消耗的时间最短，仅为9小时。
Dijkstra算法解决的是一种单源最短路径，一般是关于确定的两个点之间的最短距离的求解。与其对应的还有另一类算法用于计算多源最短路径问题，如Floyd 算法是解决任意两点间的最短路径的一种算法，可以有效处理有向图或负权（但不存在负权回路）的最短路径问题，同时也被用于计算有向图的传递闭包。
