Algs4-2.4.7大堆中第k大元素所在的位置（满树时,非满树未解决)

2.4.7在堆中，最大的元素一定在位置1上，第二大的元素一定在位置2或者3上。对于一个大小为31的堆，给出第k大的元素可能出现的位置和不可能出现的位置，其中k=2、3、4（设元素值不重复)。
解：
堆是满树时:
堆有f层,f=log(n+1)。以任意结点为根的子树都是满树，以第k大结点为根的子树的最高满子树有fc层，fc=下取整(log(n-k+1+1)),那么第k大结点在堆中的最高层为ftop,ftop=堆层f-最高满子树层fc+1=f-fc+1。


第k大结点在堆中沿简单路径放置时，最低可以放在第k层，由于堆只有f层，所以第k大结点所在的最低层fbot=min(k,f)。


那么第k大元素所在的层fk的范围是：ftop<=fk<=fbot。

第k大元素可以在其所在层的任意位置上放置，这个可以通过交换其兄弟子树的位置 和 其层层父结点的子树和其层层父结点兄弟的子树的方式得到。


那么最终得到在堆是满树时，第k大元素可以放在fk层的所有位置，位置pk的范围为：2^ftop<=pk<2^fbot


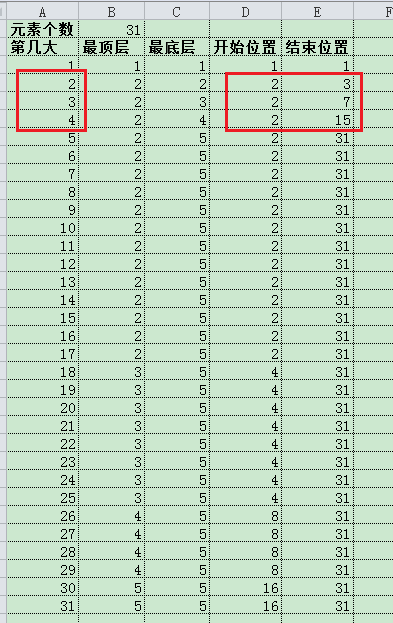
excel表计算结果如下：

公式说明:
最顶层=CEILING(LOG(2*($B$1+1)/($B$1-A3+2),2),1)
最底层=MIN(A3,LOG($B$1+1,2))
开始位置=POWER(2,B3-1)
结束位置=POWER(2,C3)-1

堆不是满树时：
分析不出。