Algs4-2.1.35不均匀的概率分布
2.1.35不均匀的概率分布。编写一个测试用例,使用非均匀分布的概率来生成随机排列数据,包括:
1)高斯分布;
2)泊松分布;
3)几何分布;
4)离散分布(一种特殊情况请见练习2.1.28)。
评估并验证这些输入数据对本节讨论的算法的性能的影响。
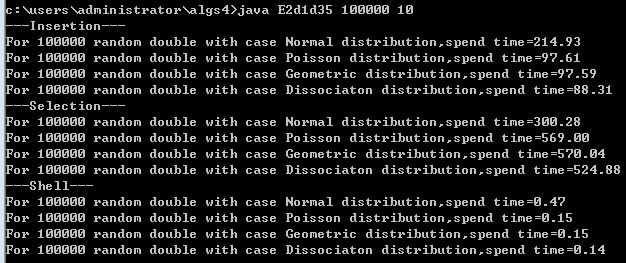
插入排序时高斯分布时间两倍于泊松分布、几何分布、离散分布。
选择排序时高斯分布约半倍于泊松分布、几何分布、离散分布。后三者时间相当,但比起选择排序性能要差6倍。
希尔排序一如即往性能远超选择排序和插入排序高斯分布时性能比另外三个慢3倍。
public class E2d1d35
{
public static double time (String alg,Double[] a)
{
Stopwatch timer =new Stopwatch();
if(alg.equals("Insertion")) Insertion.sort(a);
if(alg.equals("Selection")) Selection.sort(a);
if(alg.equals("Shell")) Shell.sort(a);
// if(alg.equals("Merge")) Merge.sort(a);
// if(alg.equals("Quick")) Quick.sort(a);
// if(alg.equals("Heap")) Heap.sort(a);
return timer.elapsedTime();
}
public static double timeRandomInput(String alg,int N,int T,int probabilityTYPE)
{
double total =0.0;
Double[] a=new Double[N];
//probabilityTYPE=0 Normal distribution
if (probabilityTYPE==0)
{
for (int t=0;t<T;t++)
{
generateNormalDistribution(a);
total+=time(alg,a);
}
}
//probabilityTYPE=1 Poisson distribution
if (probabilityTYPE==1)
{
for (int t=0;t<T;t++)
{
generatePoissonDistribution( a);
total+=time(alg,a);
}
}
//probabilityTYPE=2 Geometric distribution
if (probabilityTYPE==2)
{
for (int t=0;t<T;t++)
{
generatePoissonDistribution( a);
total+=time(alg,a);
}
}
//probabilityTYPE=3 Dissociaton distribution
if (probabilityTYPE==3)
{
for (int t=0;t<T;t++)
{
generateDissociatonDistribution(a);
total+=time(alg,a);
}
}
return total;
}//end timeRandomInput
public static void generateNormalDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=StdRandom.gaussian();
}
public static void generatePoissonDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.poisson(0.5);
}
public static void generateGeometricDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.geometric(0.5);
}
public static void generateDissociatonDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.uniform(0,2);
}
public static void main(String[] args)
{
Integer N=Integer.parseInt(args[0]);
Integer T=Integer.parseInt(args[1]);
String[] CASEmem=new String[4];
CASEmem[0]="Normal distribution";
CASEmem[1]="Poisson distribution";
CASEmem[2]="Geometric distribution";
CASEmem[3]="Dissociaton distribution";
Double time;
StdOut.printf("---Insertion---\n");
time=timeRandomInput("Insertion",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Insertion",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Insertion",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Insertion",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
StdOut.printf("---Selection---\n");
time =timeRandomInput("Selection",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Selection",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Selection",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Selection",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
StdOut.printf("---Shell---\n");
time =timeRandomInput("Shell",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Shell",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Shell",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Shell",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
}
}
1)高斯分布;
2)泊松分布;
3)几何分布;
4)离散分布(一种特殊情况请见练习2.1.28)。
评估并验证这些输入数据对本节讨论的算法的性能的影响。
插入排序时高斯分布时间两倍于泊松分布、几何分布、离散分布。
选择排序时高斯分布约半倍于泊松分布、几何分布、离散分布。后三者时间相当,但比起选择排序性能要差6倍。
希尔排序一如即往性能远超选择排序和插入排序高斯分布时性能比另外三个慢3倍。

public class E2d1d35
{
public static double time (String alg,Double[] a)
{
Stopwatch timer =new Stopwatch();
if(alg.equals("Insertion")) Insertion.sort(a);
if(alg.equals("Selection")) Selection.sort(a);
if(alg.equals("Shell")) Shell.sort(a);
// if(alg.equals("Merge")) Merge.sort(a);
// if(alg.equals("Quick")) Quick.sort(a);
// if(alg.equals("Heap")) Heap.sort(a);
return timer.elapsedTime();
}
public static double timeRandomInput(String alg,int N,int T,int probabilityTYPE)
{
double total =0.0;
Double[] a=new Double[N];
//probabilityTYPE=0 Normal distribution
if (probabilityTYPE==0)
{
for (int t=0;t<T;t++)
{
generateNormalDistribution(a);
total+=time(alg,a);
}
}
//probabilityTYPE=1 Poisson distribution
if (probabilityTYPE==1)
{
for (int t=0;t<T;t++)
{
generatePoissonDistribution( a);
total+=time(alg,a);
}
}
//probabilityTYPE=2 Geometric distribution
if (probabilityTYPE==2)
{
for (int t=0;t<T;t++)
{
generatePoissonDistribution( a);
total+=time(alg,a);
}
}
//probabilityTYPE=3 Dissociaton distribution
if (probabilityTYPE==3)
{
for (int t=0;t<T;t++)
{
generateDissociatonDistribution(a);
total+=time(alg,a);
}
}
return total;
}//end timeRandomInput
public static void generateNormalDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=StdRandom.gaussian();
}
public static void generatePoissonDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.poisson(0.5);
}
public static void generateGeometricDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.geometric(0.5);
}
public static void generateDissociatonDistribution(Double[] a)
{
for (int i=0;i<a.length;i++)
a[i]=1.0*StdRandom.uniform(0,2);
}
public static void main(String[] args)
{
Integer N=Integer.parseInt(args[0]);
Integer T=Integer.parseInt(args[1]);
String[] CASEmem=new String[4];
CASEmem[0]="Normal distribution";
CASEmem[1]="Poisson distribution";
CASEmem[2]="Geometric distribution";
CASEmem[3]="Dissociaton distribution";
Double time;
StdOut.printf("---Insertion---\n");
time=timeRandomInput("Insertion",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Insertion",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Insertion",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Insertion",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
StdOut.printf("---Selection---\n");
time =timeRandomInput("Selection",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Selection",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Selection",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Selection",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
StdOut.printf("---Shell---\n");
time =timeRandomInput("Shell",N,T,0);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[0],time);
time =timeRandomInput("Shell",N,T,1);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[1],time);
time =timeRandomInput("Shell",N,T,2);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[2],time);
time =timeRandomInput("Shell",N,T,3);
StdOut.printf("For %d random double with case %s,spend time=%.2f\n",N,CASEmem[3],time);
}
}



