Algs4-1.2.16有理数

 1.2.16有理数。为有理数实现一个可变数据类型Rational,支持加减乘除操作。无需测试溢出(请见练习1.2.17),只需使用两个long型实例变量表示分子和分母来控制溢出的可能性。使用欧几里得算法来保证分子和分母没有公因子。编写一个测试用例检测你实现的所有方法。
public class Rational
Rational(int numerator. int denominator)
Rational plus(Rational b) 该数与b之和
Rational minus(Rational b) 该数与b之差
Rational times(Rational b) 该数与b之积
Rational divides(Rational b) 该数与b之商
boolean equals(Rational that) 该数与that相等吗
String toString() 对象的字符串表示
答：


public class Rational
{
   private final long myNumerator;
   private final long myDenominator;
 
   private long gcd(long p,long q)
   {
       if (q==0) return p;
       return gcd(q,p%q);
   }
 
   public Rational(long numerator, long denominator)
    {
       long gcdValue=gcd(numerator,denominator);
       myNumerator=numerator/gcdValue;
       myDenominator=denominator/gcdValue;
    }
  
   public long Numberator()
   {
       return myNumerator;
   }
 
   public long Denominator()
   {
       return myDenominator;
   }
 
    public Rational plus(Rational b)
    {
        long gcdValue=gcd(this.Denominator(),b.Denominator());
        long n=this.Numberator()*b.Denominator()/gcdValue+b.Numberator()*this.Denominator()/gcdValue;
        long d=this.Denominator()*b.Denominator()/gcdValue;
        //
        gcdValue=gcd(d,n);
        n=n/gcdValue;
        d=d/gcdValue;
        return new Rational(n,d);
     }
  
     public Rational minus(Rational b)
    {
        long gcdValue=gcd(this.Denominator(),b.Denominator());
        long n=this.Numberator()*b.Denominator()/gcdValue-b.Numberator()*this.Denominator()/gcdValue;
        long d=this.Denominator()*b.Denominator()/gcdValue;
        //
        gcdValue=gcd(d,n);
        n=n/gcdValue;
        d=d/gcdValue;
        return new Rational(n,d);
     }
   
      public Rational times(Rational b)
    {
        long gcdValue1=gcd(this.Numberator(),b.Denominator());
        long gcdValue2=gcd(this.Denominator(),b.Numberator());
        //
        long n=this.Numberator()/gcdValue1*b.Numberator()/gcdValue2;
        long d=this.Denominator()/gcdValue2*b.Denominator()/gcdValue1;
        return new Rational(n,d);
     }
  
      public Rational divides(Rational b)
    {
        long gcdValue1=gcd(this.Numberator(),b.Numberator());
        long gcdValue2=gcd(this.Denominator(),b.Denominator());
        //
        long n=this.Numberator()/gcdValue1*b.Denominator()/gcdValue2;
        long d=this.Denominator()/gcdValue2*b.Numberator()/gcdValue1;
        return new Rational(n,d);
     }

      public boolean equals(Rational that)
    {
        if(this==that) return true;
        if(that==null) return false;
        if(this.Numberator()!=that.Numberator()) return false;
        if(this.Denominator()!=that.Denominator()) return false;
        return true;
    }

    public String toString()
    {
        return this.Numberator()+"/"+this.Denominator();
     }
  
    public static void main(String[] args)
    {
        long Numberator=Long.parseLong(args[0]);
        long Denominator=Long.parseLong(args[1]);
    
        Rational r1=new Rational(Numberator,Denominator);
        Rational r2=new Rational(Numberator,Denominator);
        //=
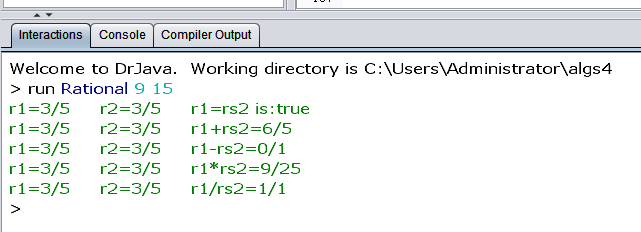
        StdOut.printf("r1=%-7s r2=%-7s r1=rs2 is:%s\n",r1.toString(),r2.toString(),r1.equals(r2));
        //+
        StdOut.printf("r1=%-7s r2=%-7s r1+rs2=%-7s\n",r1.toString(),r2.toString(),r1.plus(r2));
        //-
        StdOut.printf("r1=%-7s r2=%-7s r1-rs2=%-7s\n",r1.toString(),r2.toString(),r1.minus(r2));
        //*
        StdOut.printf("r1=%-7s r2=%-7s r1*rs2=%-7s\n",r1.toString(),r2.toString(),r1.times(r2));
        // /
        StdOut.printf("r1=%-7s r2=%-7s r1/rs2=%-7s\n",r1.toString(),r2.toString(),r1.divides(r2));
      
    }
}