奇异值分解（SVD）方法求解最小二乘问题的原理

@

目录

• 一、奇异值分解(SVD)原理
  • 1.1 回顾特征值和特征向量
  • 1.2 SVD的定义
  • 1.3 求出SVD分解后的U,Σ,V矩阵
  • 1.4 SVD计算举例
  • 1.5 SVD的一些性质
  • 1.6 SVD用于PCA
• 二、线性最小二乘问题
  • 2.1 最小二乘问题复习
  • 2.2 广义逆矩阵
  • 2.2 奇异值分解与线性最小二乘问题
• 三、SVD分解求解超定方程Ax=0（比二更简便的结论）
• 参考链接
• 打赏

一、奇异值分解(SVD)原理

1.1 回顾特征值和特征向量

　　　　我们首先回顾下特征值和特征向量的定义如下：

\[Ax=λx \]

其中A是一个n×n的实对称矩阵，x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x是矩阵A的特征值λ所对应的特征向量。

求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值\(λ_1≤λ_2≤...≤λ_n\),以及这n个特征值所对应的特征向量\(w_1,w_2,...,w_n\)，如果这n个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示：

\[A=WΣW^{−1} \]

其中W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。一般我们会把W的这n个特征向量标准化，即满足\(||w_i||_2=1\), 或者说\(w^T_iw_i=1\)，此时W的n个特征向量为标准正交基，满足\(W^TW=I\)，即\(W^T=W^{−1}\), 也就是说W为酉矩阵。

这样我们的特征分解表达式可以写成

\[A=WΣW^T \]

特征值和特征向量的求解可以参考：https://jingyan.baidu.com/article/27fa7326afb4c146f8271ff3.html

注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

1.2 SVD的定义

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

\[A=UΣV^T \]

其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足\(U^TU=I,V^TV=I\)。下图可以很形象的看出上面SVD的定义：

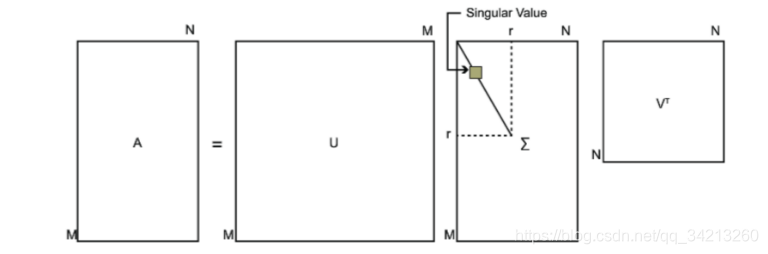
1.3 求出SVD分解后的U,Σ,V矩阵

如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵\(A^TA\)。既然\(A^TA\)是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

\[(A^TA)v_i=λ_iv_i \]

这样我们就可以得到矩阵\(A^TA\)的n个特征值和对应的n个特征向量v了。将\(A^TA\)的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵\(AA^T\)。既然\(AA^T\)是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

\[(AA^T)u_i=λ_iu_i \]

这样我们就可以得到矩阵\(AA^T\)的m个特征值和对应的m个特征向量u了。将\(AA^T\)的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

我们注意到:

\[A=UΣV^T⇒AV=UΣV^TV⇒AV=UΣ⇒Av_i=σ_iu_i⇒σ_i=Av_i/u_i \]

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

上面还有一个问题没有讲，就是我们说\(A^TA\)的特征向量组成的就是我们SVD中的V矩阵，而\(AA^T\)的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。

\[A=U \Sigma V^{T} \Rightarrow A^{T}=V \Sigma^{T} U^{T} \Rightarrow A^{T} A=V \Sigma^{T} U^{T} U \Sigma V^{T}=V \Sigma^{2} V^{T} \]

上式证明使用了:\(U^TU=I,Σ^TΣ=Σ^2\)。
可以看出\(A^TA\)的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到\(AA^T\)的特征向量组成的就是我们SVD中的U矩阵。
进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

\[\sigma_{i}=\sqrt{\lambda_{i}} \]

这样也就是说，我们可以不用\(\sigma_{i}=A v_{i} / u_{i}=\sqrt{\lambda_{i}}\)来计算奇异值，也可以通过求出\(A^TA\)的特征值取平方根来求奇异值。

1.4 SVD计算举例

这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为：

\[\mathbf{A}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\]

我们首先求出\(A^TA\)和\(AA^T\)

\[\begin{array}{c} \mathbf{A}^{\mathbf{T}} \mathbf{A}=\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)=\left(\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right) \\ \mathbf{A} \mathbf{A}^{\mathbf{T}}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)=\left(\begin{array}{lll} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1 \end{array}\right) \end{array}\]

进而求出\(A^TA\)的特征值和特征向量：

\[\lambda_{1}=3 ; v_{1}=\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) ; \lambda_{2}=1 ; v_{2}=\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)\]

接着求\(AA^T\)的特征值和特征向量：

\[\lambda_{1}=3 ; u_{1}=\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) ; \lambda_{2}=1 ; u_{2}=\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) ; \lambda_{3}=0 ; u_{3}=\left(\begin{array}{c} 1 / \sqrt{3} \\ -1 / \sqrt{3} \\ 1 / \sqrt{3} \end{array}\right)\]

利用\(Av_i=σ_iu_i,i=1,2\)求奇异值：

\[\begin{array}{l} \left(\begin{array}{cc} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)=\sigma_{1}\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) \Rightarrow \sigma_{1}=\sqrt{3} \\ \left(\begin{array}{cc} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)=\sigma_{2}\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) \Rightarrow \sigma_{2}=1 \end{array}\]

当然，我们也可以用$$\sigma_{i}=\sqrt{\lambda_{i}}$$直接求出奇异值为\(\sqrt{3}\)和1.
最终得到A的奇异值分解为：

\[A=U \Sigma V^{T}=\left(\begin{array}{ccc} 1 / \sqrt{6} & 1 / \sqrt{2} & 1 / \sqrt{3} \\ 2 / \sqrt{6} & 0 & -1 / \sqrt{3} \\ 1 / \sqrt{6} & -1 / \sqrt{2} & 1 / \sqrt{3} \end{array}\right)\left(\begin{array}{cc} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right)\]

1.5 SVD的一些性质

　　　　上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

\[A_{m \times n}=U_{m \times m} \Sigma_{m \times n} V_{n \times n}^{T} \approx U_{m \times k} \Sigma_{k \times k} V_{k \times n}^{T} \]

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵\(U_{m×k},Σ_{k×k},V^T_{k×n}\)
来表示。

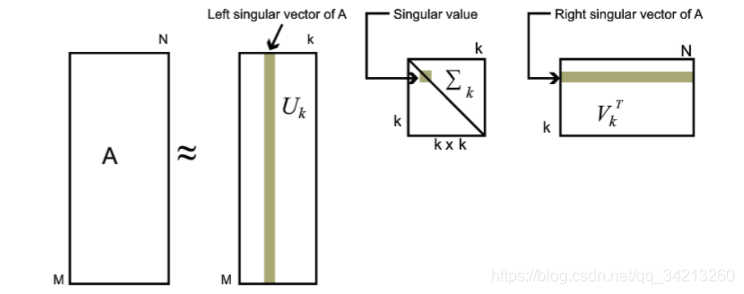
如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

1.6 SVD用于PCA

PCA降维，需要找到样本协方差矩阵\(X^TX\)的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵\(X^TX\)，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到协方差矩阵\(X^TX\)最大的d个特征向量张成的矩阵和SVD中的V矩阵是一样的，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵 \(X^TX\)，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵\(XX^T\)最大的d个特征向量张成的m×d维矩阵U，则我们如果进行如下处理：
\(X'_{d\times n}=U^T_{d\times m}X_{m\times n}\)

可以得到一个d×n的矩阵X‘,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了k，可见对行数进行了压缩。

左奇异矩阵可以用于行数的压缩。

右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

二、线性最小二乘问题

2.1 最小二乘问题复习

\[\begin{array}{l} \min \|A x-b\|_{2}^{2} \\ A \in R^{m^{* n}} \quad x \in R^{n} \quad b \in R^{m} \end{array}\]

m个方程求解n个未知数，有三种情况：

• m=n且A为非奇异，则有唯一解，\(x=A^{-1}b\)
• m>n，约束的个数大于未知数的个数，称为超定问题(overdetermined）
• m<n，负定/欠定问题（underdetermined）

通常我们遇到的都是超定问题，此时Ax=b的解是不存在的，从而转向解最小二乘问题：

\[J(x)=min \|A x-b\|_{2}^{2} \]

J(x)为凸函数，我们令一阶导数为0，得到：\(A^{T} A x-A^{T} b=0\),称之为正规方程一般解：

\[x=\left(A^{T} A\right)^{-1} A^{T} b \]

2.2 广义逆矩阵

2.2 奇异值分解与线性最小二乘问题

因为矩阵的逆很难求解，因此用SVD分解A矩阵的广义逆
对于m×n的矩阵A，其奇异值分解如下：

\[A=UΣV^T \]

根据奇异值分解，可以通过下面的计算得到广义逆：

\(A^+=(UΣV^T)^+=(ΣV^T)^+U^{−1}=VΣ^+U^T\)

其中，Σ因为是对角阵，所以广义逆就是他所有元素的倒数。可以看到这样子求解逆就十分容易了

三、SVD分解求解超定方程Ax=0（比二更简便的结论）

$Ax = 0 $ 对A做SVD分解,得\(U\Sigma V^Tx =0\)
因为是超定方程，一般无法等于0，问题转换为求最小值 =\(||U\Sigma V^Tx||_{min}\)
因为\(U\)是一个正交矩阵：正交变换不改变矩阵的秩, 特征值, 行列式, 迹 所以有：

即Ax=0的SVD解是V的最后一列

参考链接

https://www.cnblogs.com/pinard/p/6251584.html
https://zhuanlan.zhihu.com/p/131097680
https://blog.csdn.net/weixin_42587961/article/details/97374248

打赏

创作不易，如果对您有帮助，就打赏一下吧O(∩_∩)O