@
IMU与VO的融合问题可以看作是对状态量的最小二乘估计，因此核心问题就转换为了VIO 残差函数的构建。
一、系统需要优化的状态量
二、视觉重投影误差
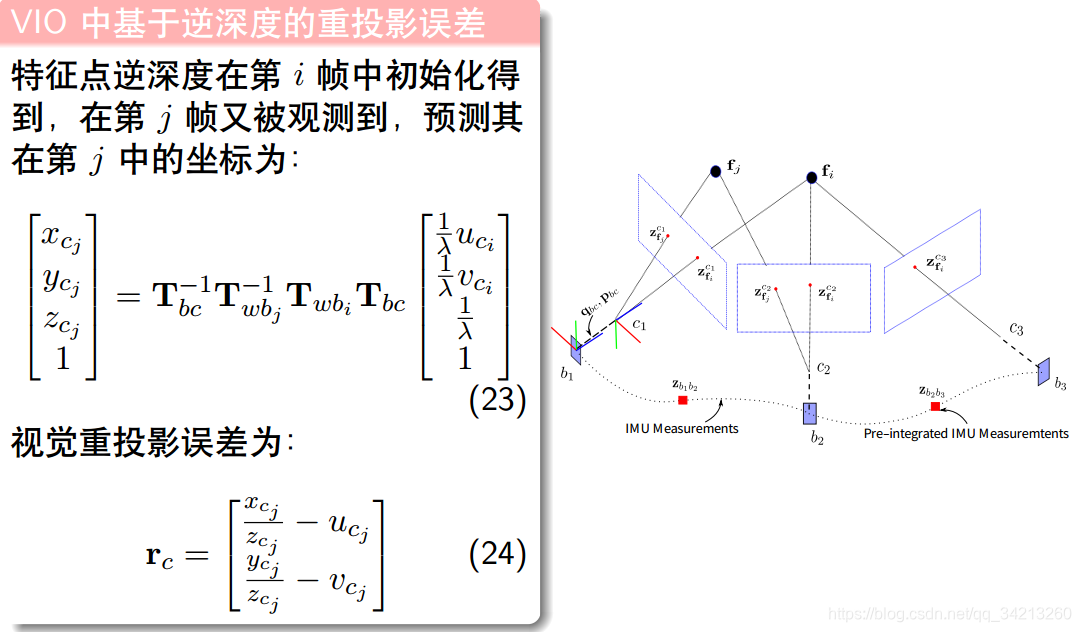
三、预积分模型
3.1 IMU 测量值的积分问题
3.2 IMU预积分模型的提出
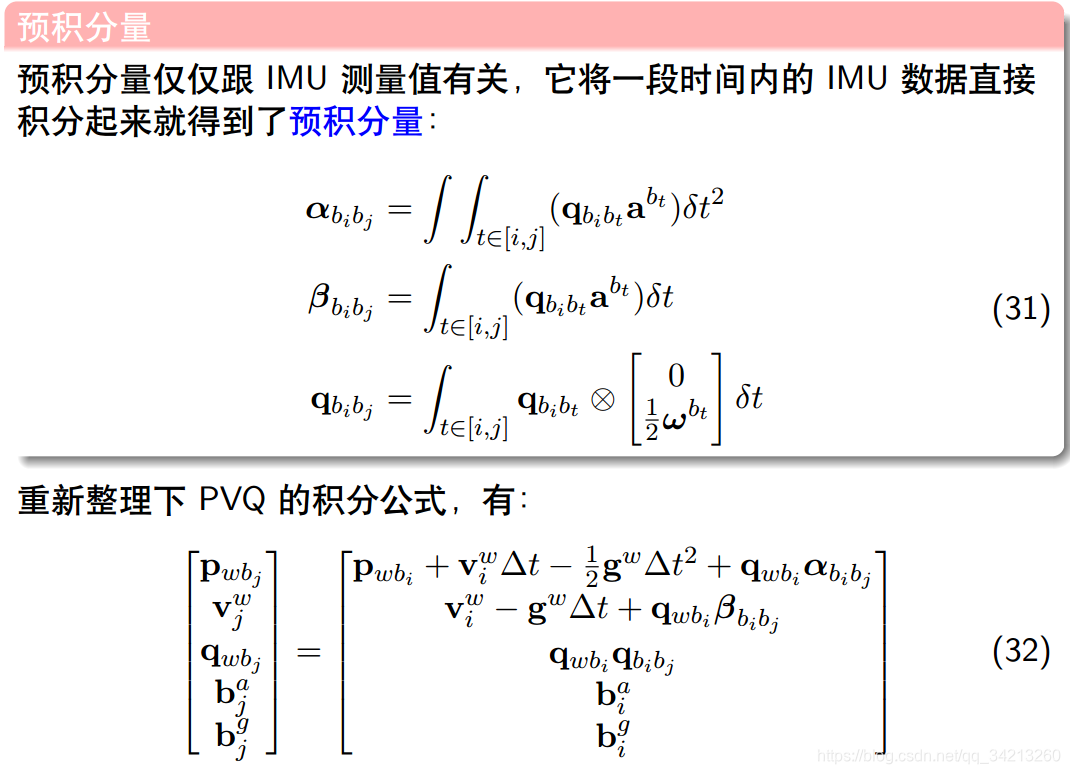
3.3 IMU 的预积分误差
第二项可以由第一章公式（7）得到
3.4 预积分的离散形式
3.5 预积分量的方差
四、状态误差线性递推公式的推导
4.1 简介
4.2 基于一阶泰勒展开的误差递推方程
4.3 基于误差随时间变化的递推方程
自己拿笔推导一下可以得到：
\(R[\delta \theta]_{×}\left(a^{b}+\delta a^{b}\right) \approx R[\delta \theta]_{×} a^{b}=R\left[a^{b}\right]_{×} \delta \theta\)
4.3 预积分的误差递推公式推导
这两个矩阵的推导从下往上推导会更简单一些
4.4 雅克比矩阵 F 的推导
F第五行推导：
\(\left\{\begin{array}{c}b_{k+1}^{g}=b_{k}^{y}+n_{b_{k}^{g}} \delta_{t} \\ \hat{b}_{k+1}+\delta b_{k+1}^{g}=\hat{b}_{k}^g+\delta b_{k}^{y}+n_{b_k^{g}} \delta t\end{array}\right.\)
\(\Rightarrow \quad \delta b_{k+1}^{g}=\delta b_{k}^{g}+n_{b_k^{g}} \delta t\)
所以可得：
\(F_{51}=0\)； \(F_{52}=0\)； \(F_{53}=0\)； \(F_{54}=0\)；\(F_{55}=I\)
同理，可得F第四行的推导：
\(F_{41}=0\)； \(F_{42}=0\)； \(F_{43}=0\)； \(F_{44}=I\)；\(F_{45}=0\)
以下推导需要知道如下公式：
- 当\(\theta\)很小时，有 \(\exp( [\boldsymbol{\theta}]_{\times})=I+ [\boldsymbol{\theta}]_{\times}\)
- \([a]_{\times}b=-[b]_{\times}a\)
第3到4行的推导需要知道如下公式：
\([\exp([\theta]_{\times})a]_{\times}=\exp([\theta]_{\times})[a]_{\times}\exp([-\theta]_{\times})\)
\(f_{34}\):对\(b^a_k\)预积分量的误差：
同上，从公式（48）易知，该Jacobian也只跟加速度有关
\(a\delta t=\frac{1}{2}\left(\mathbf{q}_{b_{i} b_{k}}\left(\mathbf{a}^{b_{k}}-\mathbf{b}_{k}^{a}\right)+\mathbf{q}_{b_{i} b_{k+1}}\left(\mathbf{a}^{b_{k+1}}-\mathbf{b}_{k}^{a}\right)\right) \delta t\)
所以Jacobian \(f_{34}=-\frac{1}{2}\left(\mathbf{q}_{b_{i} b_{k}}+\mathbf{q}_{b_{i} b_{k+1}}\right) \delta t\)
公式\(f_{35}\)有两种推导方式：
- 第一种：（第一种更容易理解）
 - 第二种
\([\mathbf{q}]_{L}[\mathbf{q}]_{R}\)这里的下标L和R表示把四元数变成对应的四元数左乘右乘的矩阵。这个式子就是四元数的旋转写成了让人看不懂的形式……(lll￢ω￢)
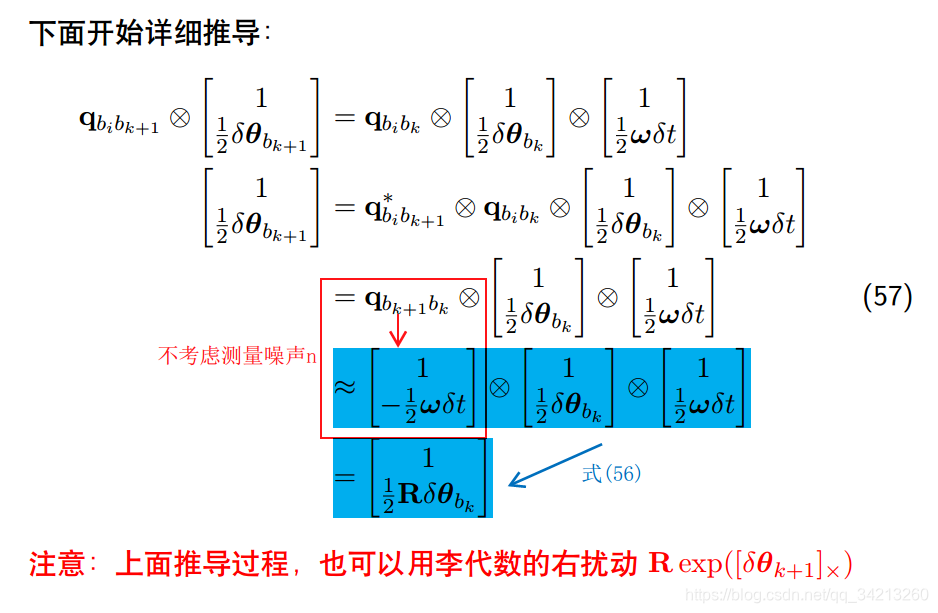
其他部分的推导过程类似
五、残差 Jacobian 的推导
5.1 视觉重投影残差的 Jacobian
上式中的 \(p\) 代表位移（也就是变换矩阵中的平移部分 t ）
\(f_c=f^w_c=f_{cw}=oc -ow\)
\(p_{bc}=t_{bc}\)因为公式（60）把平移部分和旋转部分分开来写了，所以第一个变换矩阵的旋转不影响后续的平移
公式（67）是右扰动模型
\(\frac{\partial \mathbf{f}_{\mathbf{c}_{j}}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}}=\frac{\partial \mathbf{R}_{b c}^{\top} \mathbf{R}_{w b_{j}}^{\top} \mathbf{R}_{w b_{i}}\exp(\left[\delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}\right]_{\times}) \mathbf{f}_{i_{i}}}{\partial \delta \boldsymbol{\theta}_{b_{i} b_{i}^{\prime}}}=…\)
公式（71）\(f_{cj}\)的平移部分 = \(\mathbf{R}_{b c}^{\top}\left(\mathbf{R}_{w b_{j}}^{\top}\left(\left(\mathbf{R}_{w b_{i}} \mathbf{p}_{b c}+\mathbf{p}_{w b_{i}}\right)-\mathbf{p}_{w b_{j}}\right)-\mathbf{p}_{b c}\right)=\)
5.2 IMU 误差相对于优化变量的 Jacobian
浙公网安备 33010602011771号