李群和李代数

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

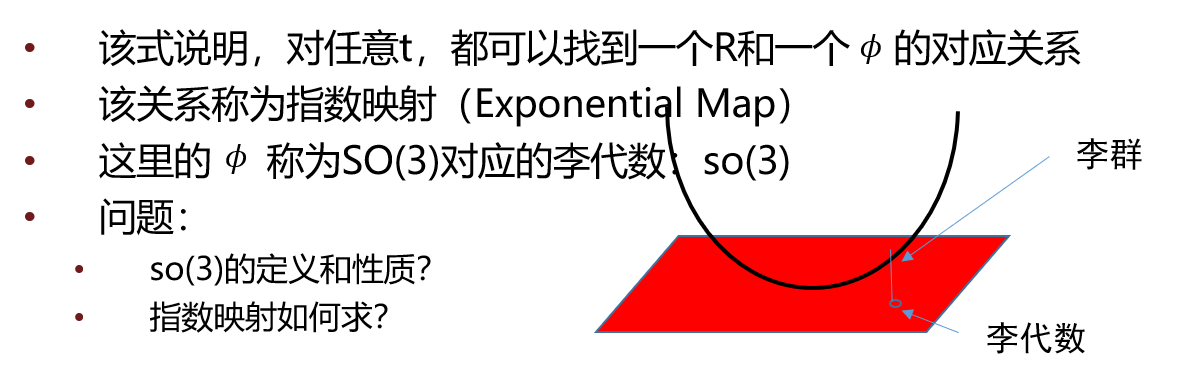
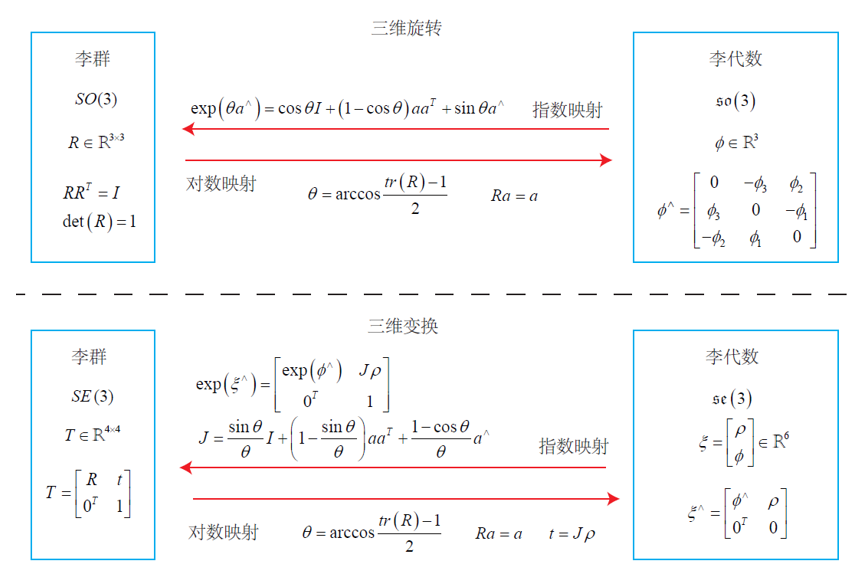
 注意：！！！！！看书本，这里的导数是旋转之后点的坐标相对于旋转的导数 ！！！！！

 

 

 

 

 

 

 

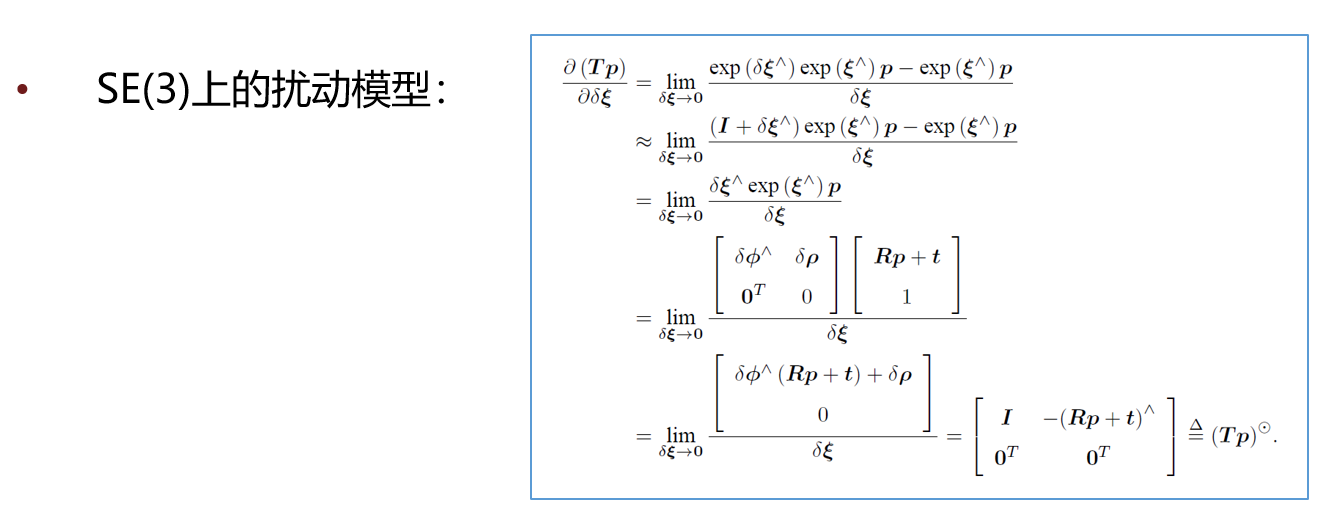
 旋转矩阵对时间的导数应为

 

 

 

 

#include <iostream>
#include <cmath>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include "sophus/se3.hpp"

using namespace std;
using namespace Eigen;

/// 本程序演示sophus的基本用法

int main(int argc, char **argv) {

  // 沿Z轴转90度的旋转矩阵
  Matrix3d R = AngleAxisd(M_PI / 2, Vector3d(0, 0, 1)).toRotationMatrix();
  // 或者四元数
  Quaterniond q(R);
  Sophus::SO3d SO3_R(R);              // Sophus::SO3d可以直接从旋转矩阵构造
  Sophus::SO3d SO3_q(q);              // 也可以通过四元数构造
  // 二者是等价的
  cout << "SO(3) from matrix:\n" << SO3_R.matrix() << endl;
  cout << "SO(3) from quaternion:\n" << SO3_q.matrix() << endl;
  cout << "they are equal" << endl;

  // 使用对数映射获得它的李代数
  Vector3d so3 = SO3_R.log();
  cout << "so3 = " << so3.transpose() << endl;
  // hat 为向量到反对称矩阵
  cout << "so3 hat=\n" << Sophus::SO3d::hat(so3) << endl;
  // 相对的，vee为反对称到向量
  cout << "so3 hat vee= " << Sophus::SO3d::vee(Sophus::SO3d::hat(so3)).transpose() << endl;

  // 增量扰动模型的更新
  Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
  Sophus::SO3d SO3_updated = Sophus::SO3d::exp(update_so3) * SO3_R;
  cout << "SO3 updated = \n" << SO3_updated.matrix() << endl;

  cout << "*******************************" << endl;
  // 对SE(3)操作大同小异
  Vector3d t(1, 0, 0);           // 沿X轴平移1
  Sophus::SE3d SE3_Rt(R, t);           // 从R,t构造SE(3)
  Sophus::SE3d SE3_qt(q, t);            // 从q,t构造SE(3)
  cout << "SE3 from R,t= \n" << SE3_Rt.matrix() << endl;
  cout << "SE3 from q,t= \n" << SE3_qt.matrix() << endl;
  // 李代数se(3) 是一个六维向量，方便起见先typedef一下
  typedef Eigen::Matrix<double, 6, 1> Vector6d;
  Vector6d se3 = SE3_Rt.log();
  cout << "se3 = " << se3.transpose() << endl;
  // 观察输出，会发现在Sophus中，se(3)的平移在前，旋转在后.
  // 同样的，有hat和vee两个算符
  cout << "se3 hat = \n" << Sophus::SE3d::hat(se3) << endl;
  cout << "se3 hat vee = " << Sophus::SE3d::vee(Sophus::SE3d::hat(se3)).transpose() << endl;

  // 最后，演示一下更新
  Vector6d update_se3; //更新量
  update_se3.setZero();
  update_se3(0, 0) = 1e-4d;
  Sophus::SE3d SE3_updated = Sophus::SE3d::exp(update_se3) * SE3_Rt;
  cout << "SE3 updated = " << endl << SE3_updated.matrix() << endl;

  return 0;
}