BP神经网络

1986年，Rumelhart等提出了误差反向传播神经网络，简称BP网络（Back Propagation），该网络是一种单向传播的多层前向网络。误差反向传播的BP算法简称BP算法，其基本思想是梯度下降法。它采用梯度搜索技术，以期使网络的实际输出值与期望输出值的误差均方值为最小。

含一个隐含层的BP网络结构如图7-5所示，图中  为输入层神经元，为隐层神经元，为输出层神经元。

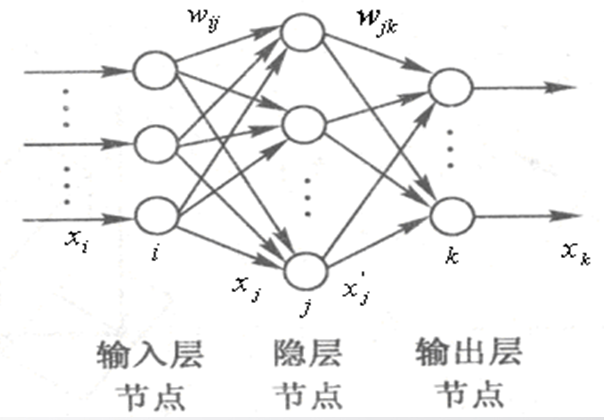
一、BP网络逼近的结构

BP网络逼近的结构如图所示，图中k为网络的迭代步骤，u(k)和y(k)为逼近器的输入。BP为网络逼近器，y(k)为被控对象实际输出，yn(k)为BP的输出。将系统输出y(k)及输入u(k)的值作为逼近器BP的输入，将系统输出与网络输出的误差作为逼近器的调整信号。

二、BP网络的优缺点

 BP网络的优点为：

（1）只要有足够多的隐层和隐层节点，BP网络可以逼近任意的非线性映射关系；

（2）BP网络的学习算法属于全局逼近算法，具有较强的泛化能力。

（3）BP网络输入输出之间的关联信息分布地存储在网络的连接权中，个别神经元的损坏只对输入输出关系有较小的影响，因而BP网络具有较好的容错性。

BP网络的主要缺点为：

（1）待寻优的参数多，收敛速度慢；

（2）目标函数存在多个极值点，按梯度下降法进行学习，很容易陷入局部极小值；

（3）难以确定隐层及隐层节点的数目。目前，如何根据特定的问题来确定具体的网络结构尚无很好的方法，仍需根据经验来试凑。

应用：

 

由于BP网络具有很好的逼近非线性映射的能力，该网络在模式识别、图像处理、系统辨识、函数拟合、优化计算、最优预测和自适应控制等领域有着较为广泛的应用。

 

由于BP网络具有很好的逼近特性和泛化能力，可用于神经网络控制器的设计。但由于BP网络收敛速度慢，难以适应实时控制的要求。

三、BP网络逼近仿真实例

使用BP网络逼近对象：

 

%BP identification
clear all;
close all;

xite=0.50;
alfa=0.05;

w2=rands(6,1);
w2_1=w2;w2_2=w2_1;

w1=rands(2,6);
w1_1=w1;w1_2=w1;

dw1=0*w1;

x=[0,0]';

u_1=0;
y_1=0;

I=[0,0,0,0,0,0]';
Iout=[0,0,0,0,0,0]';
FI=[0,0,0,0,0,0]';

ts=0.001;
for  k=1:1:1000
   
time(k)=k*ts;
u(k)=0.50*sin(3*2*pi*k*ts);
y(k)=u_1^3+y_1/(1+y_1^2);

for  j=1:1:6   
     I(j)=x'*w1(:,j);
     Iout(j)=1/(1+exp(-I(j)));
end   

yn(k)=w2'*Iout;         % Output of NNI networks

e(k)=y(k)-yn(k);    % Error calculation

w2=w2_1+(xite*e(k))*Iout+alfa*(w2_1-w2_2);

for j=1:1:6
   FI(j)=exp(-I(j))/(1+exp(-I(j)))^2;
end

for i=1:1:2
   for j=1:1:6
      dw1(i,j)=e(k)*xite*FI(j)*w2(j)*x(i);
   end
end
w1=w1_1+dw1+alfa*(w1_1-w1_2);

%%%%%%%%%%%%%%Jacobian%%%%%%%%%%%%%%%%
yu=0;
for j=1:1:6
   yu=yu+w2(j)*w1(1,j)*FI(j);
end
dyu(k)=yu;

x(1)=u(k);
x(2)=y(k);

w1_2=w1_1;w1_1=w1;
w2_2=w2_1;w2_1=w2;
u_1=u(k);
y_1=y(k);
end
figure(1);
plot(time,y,'r',time,yn,'b');
xlabel('times');ylabel('y and yn');
figure(2);
plot(time,y-yn,'r');
xlabel('times');ylabel('error');
figure(3);
plot(time,dyu);
xlabel('times');ylabel('dyu');