Codeforces Round #361 (Div. 2) D.Friends and Subsequences （multiset + 尺取法）

D. Friends and Subsequences

 

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except programming. Today they have a problem they cannot solve on their own, but together (with you) — who knows?

Every one of them has an integer sequences a and b of length n. Being given a query of the form of pair of integers (l, r), Mike can instantly tell the value of 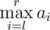 while !Mike can instantly tell the value of .

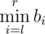Now suppose a robot (you!) asks them all possible different queries of pairs of integers (l, r) (1 ≤ l ≤ r ≤ n) (so he will make exactlyn(n + 1) / 2 queries) and counts how many times their answers coincide, thus for how many pairs 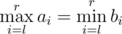 is satisfied.

How many occasions will the robot count?

Input

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbers a1, a2, ..., an ( - 109 ≤ ai ≤ 109) — the sequence a.

The third line contains n integer numbers b1, b2, ..., bn ( - 109 ≤ bi ≤ 109) — the sequence b.

Output

Print the only integer number — the number of occasions the robot will count, thus for how many pairs 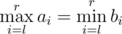 is satisfied.

Examples

input

6
1 2 3 2 1 4
6 7 1 2 3 2

output

2

input

3
3 3 3
1 1 1

output

0

Note

The occasions in the first sample case are:

1.l = 4,r = 4 since max{2} = min{2}.

2.l = 4,r = 5 since max{2, 1} = min{2, 3}.

There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.

 

#include<cstdio>
#include<set>
#include<iostream>
using namespace std;
const int maxn = 200010;
#define ll long long
int a[maxn], b[maxn];

int main() {
    int n;
    while(~scanf("%d", &n)) {
        multiset<int> sa[2];
        multiset<int> sb[2];
        for(int i = 0; i < n; i++) scanf("%d", &a[i]);
        for(int i = 0; i < n; i++) scanf("%d", &b[i]);
        int r1, r2;
        r1 = r2 = n - 1;
        ll ans = 0;
        for(int i = n - 1; i >= 0; i--) {
            sa[0].insert(a[i]); sa[1].insert(a[i]);
            sb[0].insert(b[i]); sb[1].insert(b[i]);
            while(!sa[0].empty() && *sa[0].rbegin() > *sb[0].begin()) {
                sa[0].erase(sa[0].find(a[r1]));
                sb[0].erase(sb[0].find(b[r1--]));
            }
            while(!sa[1].empty() && *sa[1].rbegin() >= *sb[1].begin()) {
                sa[1].erase(sa[1].find(a[r2]));
                sb[1].erase(sb[1].find(b[r2--]));
            }
            ans += r1 - r2;
        }
        printf("%I64d\n", ans);
    }
}