CSUST--3.21排位周赛第五场 (全解)
emmm,题目感觉都是思维题,我没有思维。。。蒟蒻的我等死了
题目链接:http://acm.csust.edu.cn/contest/80/problems
比赛过后无法提交,请到problem中提交
题目说明:
A.红黑树(简单贪心)
B.厂里吃鸡王(最短路|BFS)
C.战域(简单思维)
D.摆蔬菜2(简单思维)
E.摆蔬菜1(线段树)
红黑树
题目大意:给你一个字符串序列,只含r和b,你有两种操作
1.交换任意两个字母的位置
2.修改任意的字母
你的目标是用最少的步骤使得字符串不存在相邻的字符相同,问最小步骤是多少
Sample Input
5 brbbb
Sample Output
1
emmm,题目看起来有点唬人。。。红黑树,nmd乱来,实际上就是个简单的贪心而已,字符串不存在相邻字母相同的情况且该字符串只含2种字符,那么久只有两种情况了
1.rbrbrbrb...
2.brbrbrbr...
我们只需要将这两种情况列出来然后与给定的字符串进行对比看看哪里不一样就好了,计算一下有多少个r的位置不对$nb_r$,有多少个b的位置不对$nb_b$,那么我们可以将r和b互换,同时利用第二个操作将剩下的r或b修改掉,也就是说总的步骤就是$max(nb_r,nb_b)$。然后取两种情况的最小值就行了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e6+10; char s[mac],s1[mac],s2[mac];//rbrb,brbr int main() { int n; scanf ("%d",&n); scanf ("%s",s); int flag=0; for (int i=0; i<n; i++){ if (!flag) s1[i]='r',s2[i]='b'; else s1[i]='b',s2[i]='r'; flag^=1; } int num_b=0,num_r=0; int ans=mac; for (int i=0; i<n; i++){ if (s1[i]!=s[i]) { if (s[i]=='b') num_b++; else num_r++; } } ans=min(ans,max(num_b,num_r)); num_r=0;num_b=0; for (int i=0; i<n; i++){ if (s2[i]!=s[i]) { if (s[i]=='b') num_b++; else num_r++; } } ans=min(ans,max(num_r,num_b)); printf("%d\n",ans); return 0; }
厂里吃鸡王
题目大意:有n个建筑,m条道路(长为1),k种装备,每个建筑中有一种装备,你的任务是计算从每个建筑出发收集所有种类的装备需要多少时间,如果无法完成任务则输出0
Sample Input
8 14 5 5 2 1 3 4 4 3 3 1 3 1 5 1 6 1 3 1 2 2 2 2 4 2 2 3 8 3 6 4 8 5 6 6 8 7 7
Sample Output
5 6 5 7 7 5 0 6
emmm,题面花里胡哨的,不太想看QAQ
先做个预处理,将所有种类的装备到每个点的最短距离计算出来,也就是跑k次最短路或bfs,然后将其存入dis[k][n]中,然后。。。就没然后了。。。每种装备到每个点的最短距离都算出来了,那么该点$i$到所有装备的最短距离不就是将其全部的dis[][i]加起来吗。。。
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=5e4+10; const int inf=1e8+10; int a[mac],n; vector<int>g[mac]; int dis[105][mac]; bool vis[mac]; struct node { int id,s; }; void bfs(int x) { queue<node>q; memset(vis,false,sizeof vis); for (int i=1; i<=n; i++){ if (a[i]==x) q.push(node{i,0}),dis[x][i]=0; } while (!q.empty()){ node now=q.front(); q.pop(); if (vis[now.id]) continue; vis[now.id]=1; for (auto id:g[now.id]){ dis[x][id]=min(dis[x][id],now.s+1); q.push(node{id,dis[x][id]}); } } } int main() { int m,k; scanf ("%d%d%d",&n,&m,&k); for (int i=1; i<=n; i++){ scanf ("%d",&a[i]); } for (int i=1; i<=m; i++){ int u,v; scanf ("%d%d",&u,&v); if (u==v) continue; g[u].push_back(v); g[v].push_back(u); } memset(dis,0x3f,sizeof dis); for (int i=1; i<=k; i++) bfs(i); for (int i=1; i<=n; i++){ int ans=0; for (int j=1; j<=k; j++){ if (dis[j][i]>inf) {ans=inf; break;} ans+=dis[j][i]; } if (ans>=inf) printf("0%c",i==n?'\n':' '); else printf("%d%c",ans,i==n?'\n':' '); } return 0; }
战域
题目大意:给你n,m和n组数据(物品),你要使用m次物品,每个物品使用$x$次所需要的代价为$ax^2+bx+c$。问你最少需要多少代价(n,m<=1e5,1<=a<=1e3,-1e3<=b,c<=1e3)
Sample Input
2 3 1 1 1 2 2 2
Sample Output
13
不知道是哪个老阴比出的题目。。。你就算不使用物品也会付出$c$的代价,所以我们把所有c都加起来后这个c条件就可以直接扔了,我们每次计算每个物品的增量就好了,刚开始的时候需要将所有物品的增量都算出来,接下来使用的时候我们只需要计算使用过的物品的增量,每次去最小的增量,这里我们可以使用优先队列来取最小值

#include <bits/stdc++.h> using namespace std; const int mac=1e5+10; typedef long long ll; struct node { int a,b,c; }pt[mac]; struct HHH { int a,b,nb; ll val; bool operator<(const HHH &a)const{ return val>a.val; } }; ll solve(HHH p) { ll s1=1LL*p.a*(1LL*(p.nb+1)*(p.nb+1))+1LL*p.b*(p.nb+1); ll s2=1LL*p.a*p.nb*p.nb+1LL*p.b*p.nb; return s1-s2; } int main() { int n,m; scanf ("%d%d",&n,&m); priority_queue<HHH>q; ll ans=0; for (int i=1; i<=n; i++){ scanf ("%d%d%d",&pt[i].a,&pt[i].b,&pt[i].c); ll s=pt[i].a+pt[i].b; ans+=pt[i].c; q.push(HHH{pt[i].a,pt[i].b,1,s}); } while (m--){ HHH now=q.top(); q.pop(); ans+=now.val; ll s=solve(now);//用过一次后该物品的增量 q.push(HHH{now.a,now.b,now.nb+1,s}); } printf("%lld\n",ans); return 0; }
摆蔬菜2
题目大意:给你一个长为$n$的序列,让你选择一个不为空的子集使得该子集内的极差不超过$m$,求有多少种选择方案
Sample Input
4 7 2 4 5 100
Sample Output
8
emmm,看起来有点唬人,实际上这题也并不是很难,我们可以用团来理解一下。一个团内无论怎样组合都满足条件,那么这个团就有$2^n-1$种方案,接下来就是凑团,首先我们要对这个序列排序,设置head与tail,那么在范围[head,tail]内的我们可以称为一个团,其答案为$2^{tail-head+1}-1$。那么当head与tail变动的时候该怎么求呢?看下图:
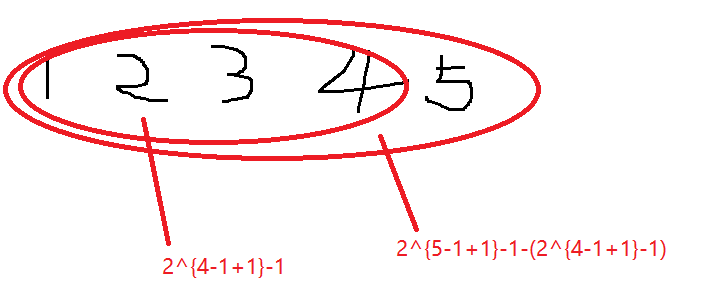
也就是说当我们将tail往后移动的时候,每移动一次我们都要计算一下答案,每次增加的数量为新的长度的数量-一部分旧长度的数量即$2^{tail-head+1}-1-(2^{tail-1-head+1}-1)=2^{tail-head}$,注意减法的时候要加上mod后在取模
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e5+10; typedef long long ll; const int mod=1e9+7; int a[mac]; ll qick(ll a,ll b) { ll ans=1; while (b){ if (b&1) ans=(ans*a)%mod; a=(a*a)%mod; b>>=1; } return ans; } int main() { int n,m; scanf ("%d%d",&n,&m); for (int i=1; i<=n; i++) scanf ("%d",&a[i]); sort(a+1,a+1+n); int head=1; ll ans=0; for (int i=1; i<=n; i++){ while (a[i]-a[head]>m) head++; ans=(ans+qick(2LL,i-head+1)-qick(2LL,i-head)+mod)%mod; } printf("%lld\n",ans); return 0; }

#include <bits/stdc++.h> using namespace std; const int mac=1e5+10; typedef long long ll; const int mod=1e9+7; int a[mac]; ll qick(ll a,ll b) { ll ans=1; while (b){ if (b&1) ans=(ans*a)%mod; a=(a*a)%mod; b>>=1; } return ans; } int main(int argc, char const *argv[]) { int n,m; scanf ("%d%d",&n,&m); for (int i=1; i<=n; i++) scanf ("%d",&a[i]); sort(a+1,a+1+n); int head=1; ll ans=0; for (int i=1; i<=n; i++){ while (a[i]-a[head]>m) head++; ans=(ans+qick(2LL,i-head))%mod; } printf("%lld\n",ans); return 0; }
摆蔬菜1
题目大意:给你一个长为$n$的序列,让你选择一段区间使得该区间的极差不大于$m$,并求该区间的最大和
Sample Input
6 2 2 1 2 1 5 3
Sample Output
8
Sample Input
2 0 4 5
Sample Output
5
emmm,签到题,一眼过去应该队列写法了,然后写到一半发现删队头的时候要考虑一些问题,有点麻烦,于是就换了无脑线段树了,噼里啪啦十分钟不到就一发A了。
写线段树的时候也要记录一下删到哪里了,这里用head表示,我们一直update将点加入到线段树中,直到不满足条件,然后head就一直往后跑一直删,直到满足条件,每次取区间和的最大值就好了。
看你比赛的时候各种方法乱飞。。。我感觉我老了
以下是AC代码(线段树写法):

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int mac=1e5+10; const int inf=1e9+10; #define lson l,mid,rt<<1 #define rson mid+1,r,rt<<1|1 struct Tree { int mx,mi; ll sum; }tree[mac<<2]; void build(int l,int r,int rt) { tree[rt].sum=0;tree[rt].mx=-inf; tree[rt].mi=inf; if (l==r) return; int mid=(l+r)>>1; build(lson);build(rson); } void update(int l,int r,int rt,int pos,int val) { if (l==r){ if (val>0) tree[rt].sum=tree[rt].mx=tree[rt].mi=val; else { tree[rt].sum=0; tree[rt].mx=-inf;tree[rt].mi=inf; } return; } int mid=(l+r)>>1; if (pos<=mid) update(lson,pos,val); else update(rson,pos,val); tree[rt].sum=tree[rt<<1].sum+tree[rt<<1|1].sum; tree[rt].mi=min(tree[rt<<1].mi,tree[rt<<1|1].mi); tree[rt].mx=max(tree[rt<<1].mx,tree[rt<<1|1].mx); } int main() { int n,m; scanf ("%d%d",&n,&m); int head=1; ll ans=0; build(1,n,1); for (int i=1; i<=n; i++){ int x; scanf ("%d",&x); update(1,n,1,i,x); while (tree[1].mx-tree[1].mi>m){ update(1,n,1,head,-1); head++; } ans=max(ans,tree[1].sum); } printf ("%lld\n",ans); return 0; }




