GIS坐标系统与投影变换【2】坐标系统的参照

有人可能会问了，你前言都不拉不拉说了那么久，怎么到现在还没有到正题，烦不烦啊~；不好意思，我这人就是比较唠叨，哼~

这里，我们先想清楚一件事情：那么多人花了那么大的力气，搞出各种坐标系来为难我们这些GIS学子，到底是为了什么？说白了，就是用来标示地球上的任何一个位置的。学过物理的我们肯定知道，所谓位置，其实是一个相对位置。相对于谁呢？——地球本身。

所以，在开始真正的正题之前，还是要先说一下在测绘上是怎么描述地球的。因为各种坐标系之间最本质的差别，其实是对地球本身描述的不同。

1.地球的形状

其实人类认识到地球是一个“球”是花了好几百万年时间的，这个就不细说了。反正现在我们已经知道的是：

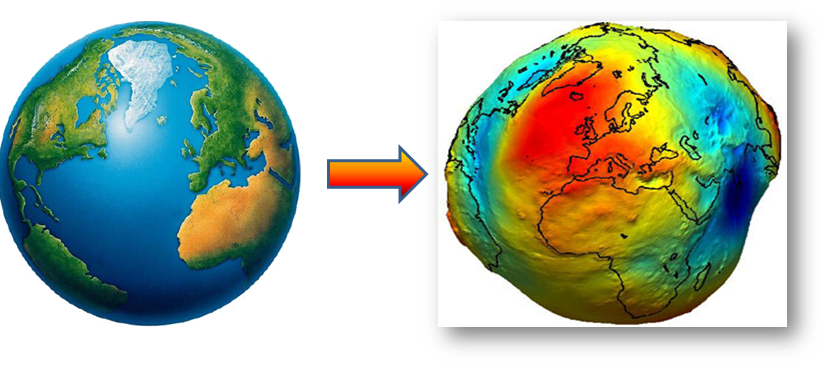
地球不是正球体。而像一个倒放着的大鸭梨，是一个两极略扁，中间略大的不规则球体。其中珠穆朗玛峰与太平洋的马里亚纳海沟之间高差近20km。

如下图所示：

2.大地水准面

为了比较好的描述地球这个不规则球体，人们先是提出了“大地水准面”。本人在上学的时候各种老师都提到过这个东东，虽然我是毕了业才大概明白的。现在，我们再回顾一下它：

大地水准面（Geoid）是一个假想的由地球自由静止的海水平面扩展延伸而形成的闭合曲面。通常是被认为是地球真实轮廓。它所包围的形体成为大地体。因为大地体的形状和大小非常接近自然地球的形状和大小，并且位置比较稳定，因此，在大范围的区域内，一般选取大地水准面作为外业测量成果的共同基准面。大地水准面这一概念最早在1873年由德国数学家利斯廷（Johann Benedict Listing）提出。
——维基百科

什么意思呢？我们应该知道，水在太空外部不受力的状态下是一个正球体。如果咱们把地球上的海洋想象成一大坨水滴，那这个大地水准面是不是应该就是个正球体呢？不是，因为地球各处密度并不均匀且引力各异，所以这个水准面在大尺度上看是一个正球，然而实际上也是凹凸不平的。最关键的问题是，地球实在不断旋转的的！！！所以这个面的形状，也是在变化的。

总而言之，利用这个面作为高精度定位的数学基础，是不靠谱的。

3.地球椭球体

为了进一步描述地球这个形状不规则、密度不均匀、还在不断瞎JB乱动的球~人们又想出了一个东东——“地球椭球体”。回顾一下概念：

维基百科：地球椭球也称地球椭球体，是在大地测量学、天文学和地球科学等领域中所使用的地球形状的数学表示。参考椭球体就是一种具有一定几何参数的地球椭球。近两百年来，科学家利用大地测量和重力测量的资料，求算出多组地球椭球参数。下表是比较常用的几个：

 

椭球名称	长半轴（米）	短半轴（m）	扁率, {\displaystyle 1/f\,\!}
克拉克（Clarke）1866	6 378 206.4	6 356 583.8	294.978 698 2
白塞尔（Bessel）1841	6 377 397.155	6 356 078.965	299.152 843 4
International 1924	6 378 388	6 356 911.9	296.999 362 1
克拉索夫斯基1940	6 378 245	6 356 863	298.299 738 1
GRS 1980	6 378 137	6 356 752.3141	298.257 222 101
WGS 1984	6 378 137	6 356 752.3142	298.257 223 563
Sphere (6371 km)	6 371 000	6 371 000	{\displaystyle \infty }