推荐领域经典算法原理回顾 (LR / FMs / DT / GBDT / XGBoost)
1. Linear Regression
以一元线性回归为例,该算法的中心思想是:找一条直线,并且让这条直线尽可能地拟合图中的数据点:
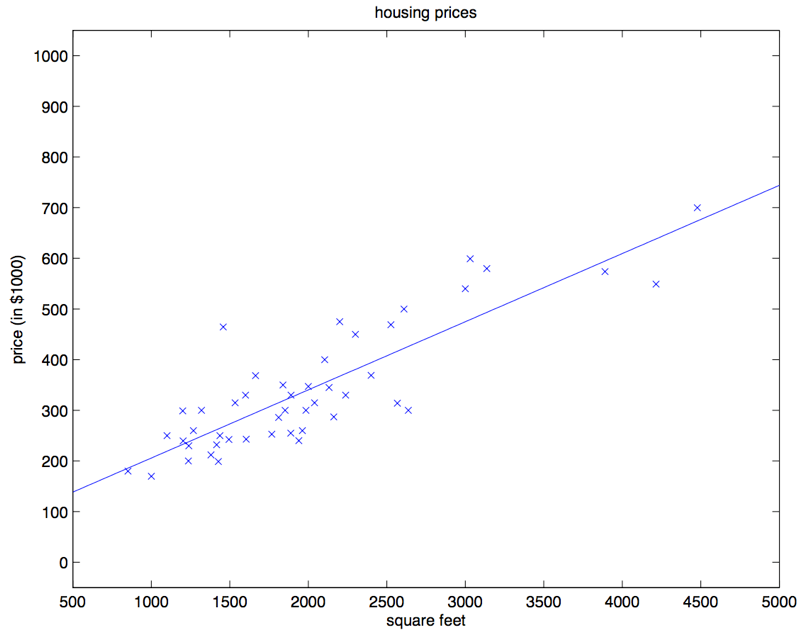
该模型可简写为:y = ax + b,我们需要根据已有的数据对(x, y),找到最佳的参数a, b 。同理,在高维空间中,我们寻找的就是线性分割空间的高维超平面。在优化模型的过程中,我们需要用损失函数 \(L(\hat y, y)\) 来衡量模型参数的好坏,线性回归常用的损失函数为均方误差(MSELoss):
\(L(\hat y, y)=\frac{1}{m} \sum_{i=1}^{m} (\hat y^{(i)} - y^{(i)})^2\)
模型训练(寻找最佳参数)的过程就是求解以下函数的过程:
\(a^*, b^* = \textstyle\arg\min_{a,b}L(\hat y, y)\)
该函数可以通过微积分和线代计算求解(最小二乘法),也可以通过最优化方法求解。在实践中,由于模型涉及的训练数据往往规模较大,如果用最小二乘法来解矩阵方程将会消耗过多的计算资源,因此我们常用最优化方法中的梯度下降法来求解该函数
梯度下降法的原理并不复杂,我们只需要从参数的初始值开始,根据训练数据的计算结果不断更新参数即可:
\(w_j := w_j - \alpha \frac{\partial }{\partial w_j}L(\omega )\)
批梯度下降和随机梯度下降都是在上述公式的基础上做的简单改进,其目在于提升算法的优化效率,这里就暂时先不展开了
2. Factorization Machines
相关Paper:
- Rendle S . Factorization Machines[C] ICDM 2010
- Rendle S , et al. Fast context-aware recommendations with factorization machines[C]
算法介绍:
- FMs的优点:
- FMs考虑了特征的二阶交叉,弥补了逻辑回归表达能力差的缺陷
- FMs模型复杂度保持为线性,并且改进为高阶特征组合时,仍为线性复杂度
- FMs引入隐向量,缓解了数据稀疏带来的参数难训练问题
- 在推荐算法的应用场景中,用户和物品特征中有很多项是categorical类型的,需要经过One-Hot编码转化成数值型特征,这将导致样本数据变得非常稀疏:

- 在推荐算法的应用场景中,用户和物品特征中有很多项是categorical类型的,需要经过One-Hot编码转化成数值型特征,这将导致样本数据变得非常稀疏:
- FMs的缺点:
- 虽然考虑了特征的交叉,但是表达能力仍然有限,不及深度模型
- 同一特征 x_i 与不同特征组合使用的都是同一隐向量 v_i ,违反了特征与不同特征组合可发挥不同重要性的事实
- 模型原理:
- FM在线性模型的基础上添加了一个多项式,用于描述特征之间的二阶交叉:
\(y = \omega _0 + \sum _{i=1}^{n} \omega _i x_i + \sum _{i=1}^{n-1} \sum _{j=i+1}^{n} \omega _{ij} x_i x_j\)- 上式中:n表示特征维数,不同特征两两组合可以得到n(n-1)/2个交叉
- 举个例子描述特征交叉:假如我们知道“小明既喜欢看战争电影,又曾购买过坦克模型”,那么我们就能比仅知道“小明喜欢看战争电影”或“小明购买过坦克模型”更能推断出小明对某军事类广告的点击倾向。从数学角度看,就是我们原本只建模f(x) = z 和 f(y) = z,现在我们能建模f(x, y) = z,这其实就是模型复杂度提升所带来的拟合能力的提升
- FM在线性模型的基础上添加了一个多项式,用于描述特征之间的二阶交叉:
- 引入交叉特征后带来的问题:
- 上式中参数w_ij的优化其实是比较困难的,因为在计算梯度时,只有x_i和x_j都不为0时,我们才能得到有效的结果,但由于特征矩阵的稀疏性,使得大部分参数w都难以得到充分的训练
- 解决方案:
-
FM对于每个特征x_i,学习一个长度为k(k << n)的一维向量v,进而得到一个n×k的矩阵V,于是,两个特征 x_i 和 x_j 的特征组合的权重值,通过特征对应的向量 v_i 和 v_j 的内积 <v_i, v_j> 来表示,等同于对特征做了一个embedding:

-
这个embedding并不依赖某个特定的特征组合是否出现过,所以只要特征 x_i 和其它任意特征组合出现过,那么就可以学习自己对应的embedding向量
-
- 复杂度分析:算法的计算复杂度为O(kn),推导和化简过程可见Rendle S . Factorization Machines中的 Lemma 3.1
- 在优化方面,随机梯度下降(SGD)和交替最小二乘(ALS)的单轮迭代复杂度都是O(kN_z(X)),ALS的优势在于它不需要指定额外的超参(学习率),因此在效果上更加稳定
3. XGBoost
GBDT是以决策树(CART)为基学习器的GB算法,XGBoost扩展和改进了GDBT,XGBoost算法更快,准确率也相对较高。我们接下来按顺序依次对其进行介绍。
先看决策树:
-
决策树模型的构造过程可概括为:循环执行“特征选择+分裂子树”,最后触达阈值停止分裂。在预测阶段,我们把样本特征按树的分裂过程依次展开,最后样本的标签就是叶子节点中占大多数的样本所对应的标签:

-
决策树如何做特征选择?—— 三种算法(ID3, C4.5, CART)
- ID3以信息熵减幅度作为特征选择依据,缺点是该算法偏好细粒度高的特征(如uuid),容易过拟合;C4.5在熵减式子中增加了一个分母(分枝数目)作为惩罚项,规避了ID3特征分裂时细粒度过高的问题;CART采用Gini系数作为特征选择依据,在保持其他算法优点的同时(Gini系数可理解为熵模型的一阶泰勒展开),减少了大量的对数运算
-
剪枝策略:
- 预剪枝:在分裂子树前判断是否继续。常用的停止标准包括:“计算分裂前后准确率是否提升”,“检查分裂后节点内样本容量是否低于阈值”等。预剪枝策略可以降低过拟合风险,减少模型训练时间,但同时也会带来欠拟合风险
- 后剪枝:在决策树构建完成后删去不必要的子树。典型的后剪枝策略如C4.5的“悲观剪枝法”:自底向上依次判断各节点分裂前后模型准确率是否提升,删去对结果无增益的子树。后剪枝策略的泛化性能常优于预剪枝策略,但其需要更多的训练时间
-
连续值处理(以CART为例):
- 在解决回归问题时,CART采用和方差作为特征分割点的选择方式:对任意有序数值特征a,穷举分割界限s,计算分割后的两团簇数据的和方差,最后取分割后和方差最小的界限作为切割阈值:
\(min_{a,s}\left [ min_{c_1} \sum_{x_i \in D_1} (y_i - c_1)^2 + min_{c_2} \sum_{x_i \in D_2} (y_i - c_2)^2\right ]\)
上式中D1,D2代表分割后的两团数据簇,c1, c2代表两团数据簇中的数据均值
- 在解决回归问题时,CART采用和方差作为特征分割点的选择方式:对任意有序数值特征a,穷举分割界限s,计算分割后的两团簇数据的和方差,最后取分割后和方差最小的界限作为切割阈值:
-
接下来我们看GB与GBDT:
- GB(Gradient boosting)是一种集成学习方法,通过聚合多个弱模型,来获得一个强模型。其核心思路是各模型通过“串联”的方式,依次拟合其前置模型的残差,进而实现对模型总体偏差(bias)的纠正。假设我们有M个弱模型,那么上述思想可用公式表述为:
\(\begin{matrix} F_{m+1}(x) = F_m(x) + h(x) , & 1 \le m \le M \end{matrix}\) - 注意上式中后置学习器拟合的h(x)是通过训练数据计算出来的,其不同于真实数据分布中的残差,为了对二者作区分,h(x)又被称作“伪残差”
- GB(Gradient boosting)是一种集成学习方法,通过聚合多个弱模型,来获得一个强模型。其核心思路是各模型通过“串联”的方式,依次拟合其前置模型的残差,进而实现对模型总体偏差(bias)的纠正。假设我们有M个弱模型,那么上述思想可用公式表述为:
-
GBDT就是用决策树(CART)充当GB方法中的弱模型(基学习器),进而实现的集成学习算法,其中基学习器的迭代步骤为:
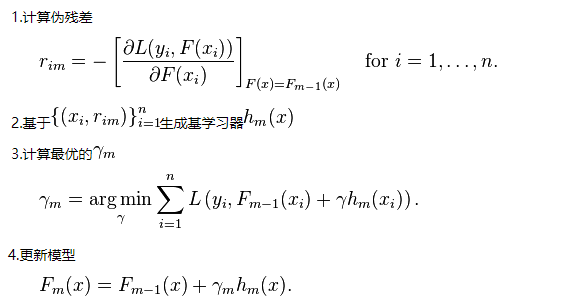
我们注意到:在第一步计算伪残差时,我们对损失函数求了一个偏导,以此作为目标残差的近似。为什么这里能用负梯度来估算残差呢?其实这里蕴含了一个隐藏条件,就是基学习器(CART)的损失函数必须为平方误差(Square Error Loss),只有这个条件满足时,我们才能用负梯度近似残差,相关数学证明可参考:GBDT理解难点 - 拟合负梯度
最后我们看XGBoost:
- XGBoost在总体思路上与GBDT是相同的,它们都是通过串联决策树来拟合残差,二者的不同之处在于目标函数的定义以及实现细节上的差异。从另一个角度看,我们也可以把XGBoost理解为工程视角下,加入了各种tricks以进行强化的GBDT
- XGBoost的目标函数推导:
- XGBoost通过叠加t个基学习器来拟合目标数据分布,从整体来看,其目标函数可分为两部分——预测误差惩罚项和模型复杂度惩罚项:
\[\begin{matrix} Obj = \sum_{i=1}^n l(\hat y_i,y_i) + \sum_{t=1}^k \Omega(f_t) & , & \Omega(f_t) = \gamma T_t + \frac{1}{2}\lambda \sum_{j=1}^T \omega _j^2 \end{matrix} \]- 上式中n代表训练样本树,函数l代表预测误差惩罚项,函数Omega代表模型复杂度惩罚项,T_t代表基学习器t下的叶子节点数目,omega代表基学习器中的权重参数(即L2正则项),gamma和lambda是平衡两个复杂度惩罚项的权重超参
- 由于Boosting需要依次对各基学习器的结果求和,所以在训练第t个模型时,算法给出的预测值为:
\[\hat y_i^t = \hat y_i^{t-1} + f_t(x_i) \]- 上式中y hat代表已构建好的基学习器的预测结果,函数f代表正在训练的基学习器,将其带入前面给出的目标函数,得到:
\[Obj^{(t)} = \sum_{i=1}^n l(\hat y_i^{t-1} + f_t(x_i),y_i) + \sum_{i=1}^t \Omega(f_i) \]- 已知泰勒二阶展开式:
\[f(x+\bigtriangleup x) \approx f(x) + f'(x) \bigtriangleup x + \frac{1}{2}f''(x)\bigtriangleup x^2 \]- 将 \(\hat y_i^t = \hat y_i^{t-1} + f_t(x_i)\) 中的第一个加项视为x,第二个加项视为delta x,对目标函数中的预测误差惩罚项做二阶泰勒展开,得到:
\[Obj^{(t)} \approx \sum_{i=1}^n \left [ l(\hat y_i^{t-1},y_i) + g_i f_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] + \sum_{i=1}^t \Omega(f_i) \]- 上式中g_i是损失函数loss()的一阶导数,h_i是损失函数的二阶导数
- 由于前置基学习器的预测结果已知,因此 \(l(\hat y_i^{t-1},y_i)\) 在式中是一个常数,其值不影响优化结果,固可从目标式中移除:
\[Obj^{(t)} \approx \sum_{i=1}^n \left [ g_i f_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] + \sum_{i=1}^t \Omega(f_i) \]- 同样,由于前置学习器的y hat已知,因此在损失函数确定后(比如指定SELoss),g_i和h_i的值也可以通过计算得出,在式中为常数。至此,目标函数中的未知量就只剩当前学习器的输出值f了。考虑到XGBoost使用的基学习器是决策树,因此遍历所有样本后对各样本的损失求和,就等同于决策树接收所有训练样本后,对各叶子节点给出的预测值计算损失并求和,即:
\[\sum_{i=1}^n \left [ g_i f_t(x_i) + \frac{1}{2}h_if_t^2(x_i) \right ] = \sum_{j=1}^T \left [ \left ( \sum_{i \in I_j} g_i \right ) \omega_j + \frac{1}{2}\left ( \sum_{i \in I_j} h_i \right ) \omega_j^2 \right ] \]这里T代表叶子节点总数,j代表叶子节点序号,I_j代表该叶子节点中的训练样本集,omega_j 代表该叶子节点给出的预测值- 将上式代入目标函数式中,并将复杂度惩罚项Omega()展开,得到:
\[\begin{aligned} Obj^{(t)} &\approx \sum_{j=1}^T \left [ \left ( \sum_{i \in I_j} g_i \right ) \omega_j + \frac{1}{2}\left ( \sum_{i \in I_j} h_i \right ) \omega_j^2 \right ] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T \omega _j^2 \\ &= \sum_{j=1}^T \left [ \left ( \sum_{i \in I_j} g_i \right ) \omega_j + \frac{1}{2}\left ( \sum_{i \in I_j} h_i + \lambda \right ) \omega_j^2 \right ] + \gamma T\\ \end{aligned} \]- 进一步,记\(\begin{matrix} G_j = \sum_{i \in I_j} g_i & , & H_j = \sum_{i \in I_j} h_i \end{matrix}\),则上述目标函数可表示为:
\[Obj^{(t)} = \sum_{j=1}^T \left [ G_j \omega_j + \frac{1}{2}\left ( H_j + \lambda \right ) \omega_j^2 \right ] + \gamma T \]- 我们可以在上式中对omega_j求一阶导,并令其等于0:
\[\frac{\partial Obj^{(t)}}{\partial\omega_j} = G_j + (H_j + \lambda)\omega_j = 0 \]- 进而将omega_j用其他已知项表达出来:
\[\omega_j^* = -\frac{G_j}{H_J + \lambda} \]- 将上式代入目标函数式,进一步化简得到:
\[obj = -\frac{1}{2}\sum^T_{j=1}\frac{G_j^2}{H_j+\lambda} + \gamma T \]该式就是我们最终使用的目标函数的形式了,上式中的G和H需要我们指定损失函数,然后分别求一阶和二阶导得到。通过该目标函数,我们即可在决策树中对特征进行选择分裂(穷举得到使目标函数下降最多的分割方案,当然,其中依然有工程上的优化tricks)。由于XGBoost的目标函数中本身有对模型复杂度的惩罚项,因此我们不需要再做额外的剪枝工作。同时,由于G和H对各训练样本间相互没有依赖,因此各样本的损失可以并行计算,从而加快了模型的训练速度。
【参考】

