命名实体识别(1) - HMM
模型介绍
马尔科夫假设: 假设模型的当前状态仅仅依赖于前面的几个状态
一个马尔科夫过程是状态间的转移仅依赖于前n个状态的过程。这个过程被称之为n阶马尔科夫模型,其中n是影响下一个状态选择的(前)n个状态。最简单的马尔科夫过程是一阶模型,它的状态选择仅与前一个状态有关。这里要注意它与确定性系统并不相同,因为下一个状态的选择由相应的概率决定,并不是确定性的。
对于有M个状态的一阶马尔科夫模型,共有\(M^2\)个状态转移,因为任何一个状态都有可能是所有状态的下一个转移状态。每一个状态转移都有一个概率值,称为状态转移概率——这是从一个状态转移到另一个状态的概率。所有的\(M^2\)个概率可以用一个状态转移矩阵表示。注意这些概率并不随时间变化而不同——这是一个非常重要(但常常不符合实际)的假设。
以天气系统为例,假设有状态转移矩阵:

要初始化这样一个系统,我们需要确定起始日天气的(或可能的)情况,定义其为一个初始概率向量,称为pi向量:

也就是说,第一天为晴天的概率为1。现在我们定义一个一阶马尔科夫过程如下:
- 状态:三个状态——晴天,多云,雨天。
- pi向量:定义系统初始化时每一个状态的概率。
- 状态转移矩阵:给定前一天天气情况下的当前天气概率。
任何一个可以用这种方式描述的系统都是一个马尔科夫过程。
在某些情况下,我们希望通过观察到的状态序列来预测某个隐藏的状态序列:比如通过观察水藻状态来预测天气,或者通过观察声带振动来预测发音单词等。在这种情况下,观察到的状态序列与隐藏过程有一定的概率关系。我们使用隐马尔科夫模型对这样的过程建模,这个模型包含了一个底层隐藏的随时间改变的马尔科夫过程,以及一个与隐藏状态某种程度相关的可观察到的状态集合。
需要着重指出的是,隐藏状态的数目与观察状态的数目可以是不同的。一个包含三个状态的天气系统(晴天、多云、雨天)中,可以观察到4种(或更少,或更多)的海藻湿润情况(干、稍干、潮湿、湿润等)
下图显示的是天气例子中的隐藏状态和观察状态:
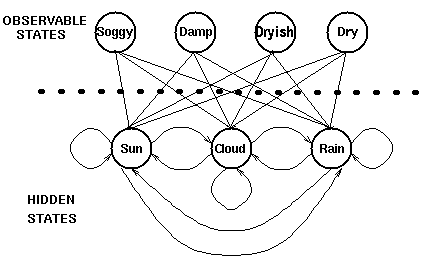
隐藏状态和观察状态之间的连接表示:在给定的马尔科夫过程中,一个特定的隐藏状态生成特定的观察状态的概率。‘进入’一个观察状态的所有概率之和为1.
除了定义了马尔科夫过程的概率关系,我们还有另一个矩阵,定义为混淆矩阵(confusion matrix),它包含了给定一个隐藏状态后得到的观察状态的概率。对于天气例子,混淆矩阵是:
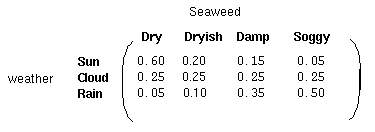
注意矩阵的每一行之和是1。
总结(Summary)
隐马尔科夫模型(HMM)包含2组状态集合和3组概率集合:
- 隐藏状态 \(N\):一个系统的(真实)状态,可以由一个马尔科夫过程进行描述(例如,天气)。
- 观察状态 \(M\):在这个过程中‘可视’的状态(例如,海藻的湿度)。
- pi向量 \(\pi\):包含了(隐)模型在时间t=1时一个特殊的隐藏状态的概率(初始概率)。
- 状态转移矩阵 \(A\):包含了一个隐藏状态到另一个隐藏状态的概率
- 混淆矩阵 \(B\):包含了给定隐马尔科夫模型的某一个特殊的隐藏状态,观察到的某个观察状态的概率。
在状态转移矩阵及混淆矩阵中的每一个概率都是时间无关的——也就是说,当系统演化时这些矩阵并不随时间改变。实际上,这是马尔科夫模型关于真实世界最不现实的一个假设。
隐马尔科夫模型通常解决的问题包括:
- 对于一个观察序列匹配最可能的系统——评估,使用前向算法(forward algorithm)解决;
- 对于已生成的一个观察序列,确定最可能的隐藏状态序列——解码,使用Viterbi 算法(Viterbi algorithm)解决;
- 对于已生成的观察序列,决定最可能的模型参数——学习,使用前向-后向算法(forward-backward algorithm)解决。
NER与Viterbi算法
NER其实就是序列标注问题,那么HMM中的5个基本元素:\(\{N,M,A,B,π\}\)在序列标注问题中可理解为:
N: 隐藏状态的有限集合。在NER任务中,是指每一个词语背后的标注。
M: 观察状态的有限集合。在NER任务中,是指每一个词语本身。
A: 状态转移矩阵。在NER任务中,是指某一个标注转移到下一个标注的概率。
B: 混淆矩阵。在NER任务中,是指在某个标注下,生成某个词的概率。
π: pi向量。在NER任务中,是指每一个标注的初始化概率。
以上的这些元素,都是可以从训练语料集中统计出来的。最后,我们根据这些统计值,应用维特比(viterbi)算法,就可以算出词语序列背后的标注序列了。
举个例子:
假设有三个词语(观察状态集合M):{'策划', '决定', '记录'}
有两种可能的标注(隐藏状态集合N): {'动词v.', '名词n.'}
句子中第一个词可能的词性(Pi向量):{'动词': 0.3, '名词': 0.7}
从语料中统计得知:一个词到下一个词之间,词性转换的比例分布 = {
名词->名词: 0.3 ,
名词->动词: 0.7 ,
动词->名词: 0.6 ,
动词->动词: 0.4
}
由此可以列出相应的状态转移矩阵A
同样,从语料中统计得知:在指定标注下,各词语出现的比例 = {
名词,策划:0.7 ,决定 :0.2 ,记录: 0.1 ;
动词,策划:0.1 ,决定 :0.5 ,记录: 0.4
}
由此可以列出相应的混淆矩阵B
已知一个句子片段分词后是:“策划 决定 记录”
那么就有\(2^3\)种可能的标注序列: nnn, nnv, nvn, nvv, vnn, vnv, vvn, vvv
我们需要寻找这些标注序列中,统计概率最大的那一组。
Viterbi算法解决该问题的思路其实就是动态规划的思路:
n个词概率最大的标注序列 = 前n-1词概率最大的标注序列 + 最后1个词概率最大的标注
按这个思路,我们来一起算一下:
P(句子第一个词是名词) = P(一般第一个词是名词) * P(名词中出现'策划') = 0.70.7 = 0.49
P(句子第一个词是动词) = P(一般第一个词是动词) * P(动词中出现'策划') = 0.30.1 = 0.03
接着,按照DP的思想:前二个词概率最大的标注等于第一个词概率最大的标注加上第二个词概率最大的标注,由于第一个词概率最大的标注我们已经算出来了,所以第二个词的标注的计算过程:
P(句子第二个词是名词|第一个词是名词) = P(第一个词是名词) * P(名词转名词) * P(名词中出现'决定') = 0.490.30.2 = 0.0294
P(句子第二个词是动词|第一个词是名词) = P(第一个词是名词) * P(名词转动词) * P(动词中出现'决定') = 0.490.70.5 = 0.1715
所以前两个词概率最大的标注序列是:[名词, 动词]
同样的,三个词概率最大的标注序列 = 前两个词概率最大的标注序列 + 最后一个词概率最大的标注
大家可以自己算一算,看看最后的结果是不是[名词,动词,动词]呢?
代码实践
数据
数据样例:
O:other, B:begin,M:middle,E:end,S:single word
1 O
9 O
9 O
8 O
年 O
9 O
月 O
马 B-ORG
钢 M-ORG
总 M-ORG
公 M-ORG
司 E-ORG
改 O
制 O
为 O
马 B-ORG
钢 M-ORG
( M-ORG
集 M-ORG
团 M-ORG
) M-ORG
控 M-ORG
股 M-ORG
有 M-ORG
限 M-ORG
公 M-ORG
司 E-ORG
, O
顾 S-NAME
先 O
生 O
出 O
任 O
总 B-TITLE
经 M-TITLE
理 E-TITLE
。 O
读取数据:
word_lists = []
tag_lists = []
with open(filepath, 'r', encoding='utf-8') as f:
word_list = []
tag_list = []
for line in f:
if line != '\n': # 句子之间通过空行分隔
word, tag = line.strip('\n').split()
word_list.append(word)
tag_list.append(tag)
else:
word_lists.append(word_list)
tag_lists.append(tag_list)
word_list = []
tag_list = []
# 如果make_vocab为True,还需要返回word2id和tag2id
if make_vocab:
word2id = build_map(word_lists)
tag2id = build_map(tag_lists)
return word_lists, tag_lists, word2id, tag2id
else:
return word_lists, tag_lists
# 构建词表,按每个词的出现顺序建立数字索引
def build_map(lists):
maps = {}
for list in lists:
for element in list:
if element not in maps:
maps[e] = len(maps) # 确保每个词都有唯一的数字索引
return maps
模型
构建HMM模型:
import torch
class HMM(object):
def __init__(self, N, M):
"""Args:
N: 状态数,这里对应存在的标注的种类
M: 观测数,这里对应数据集中有多少不同的字
"""
self.N = N
self.M = M
# 状态转移概率矩阵 A[i][j]表示从i状态转移到j状态的概率
self.A = torch.zeros(N, N)
# 观测概率矩阵, B[i][j]表示i状态下生成j观测的概率
self.B = torch.zeros(N, M)
# 初始状态概率 Pi[i]表示初始时刻为状态i的概率
self.Pi = torch.zeros(N)
def train(self, word_lists, tag_lists, word2id, tag2id):
"""HMM的训练,即根据训练语料对模型参数进行估计,
因为我们有观测序列以及其对应的状态序列,所以我们
可以使用极大似然估计的方法来估计隐马尔可夫模型的参数
参数:
word_lists: 列表,其中每个元素由字组成的列表,如 ['担','任','科','员']
tag_lists: 列表,其中每个元素是由对应的标注组成的列表,如 ['O','O','B-TITLE', 'E-TITLE']
word2id: 将字映射为ID
tag2id: 字典,将标注映射为ID
"""
assert len(tag_lists) == len(word_lists)
# 估计转移概率矩阵
for tag_list in tag_lists:
seq_len = len(tag_list)
for i in range(seq_len - 1):
current_tagid = tag2id[tag_list[i]]
next_tagid = tag2id[tag_list[i+1]]
self.A[current_tagid][next_tagid] += 1
# 问题:如果某元素没有出现过,该位置为0,这在后续的计算中是不允许的
# 解决方法:我们将等于0的概率加上很小的数
self.A[self.A == 0.] = 1e-10
self.A = self.A / self.A.sum(dim=1, keepdim=True)
# 估计观测概率矩阵
for tag_list, word_list in zip(tag_lists, word_lists):
assert len(tag_list) == len(word_list)
for tag, word in zip(tag_list, word_list):
tag_id = tag2id[tag]
word_id = word2id[word]
self.B[tag_id][word_id] += 1
self.B[self.B == 0.] = 1e-10
self.B = self.B / self.B.sum(dim=1, keepdim=True)
# 估计初始状态概率
for tag_list in tag_lists:
init_tagid = tag2id[tag_list[0]]
self.Pi[init_tagid] += 1
self.Pi[self.Pi == 0.] = 1e-10
self.Pi = self.Pi / self.Pi.sum()
def test(self, word_lists, word2id, tag2id):
pred_tag_lists = []
for word_list in word_lists:
pred_tag_list = self.decoding(word_list, word2id, tag2id)
pred_tag_lists.append(pred_tag_list)
return pred_tag_lists
def decoding(self, word_list, word2id, tag2id):
"""
使用维特比算法对给定观测序列求状态序列, 这里就是对字组成的序列,求其对应的标注。
维特比算法实际是用动态规划解隐马尔可夫模型预测问题,即用动态规划求概率最大路径(最优路径)
这时一条路径对应着一个状态序列
"""
# 问题:整条链很长的情况下,十分多的小概率相乘,最后可能造成下溢
# 解决办法:采用对数概率,这样源空间中的很小概率,就被映射到对数空间的大的负数
# 同时相乘操作也变成简单的相加操作
A = torch.log(self.A)
B = torch.log(self.B)
Pi = torch.log(self.Pi)
# 初始化 维比特矩阵viterbi 它的维度为[状态数, 序列长度]
# 其中viterbi[i, j]表示标注序列的第j个标注为i的所有单个序列(i_1, i_2, ..i_j)出现的概率最大值
seq_len = len(word_list)
viterbi = torch.zeros(self.N, seq_len)
# backpointer是跟viterbi一样大小的矩阵
# backpointer[i, j]存储的是 标注序列的第j个标注为i时,第j-1个标注的id
# 等解码的时候,我们用backpointer进行回溯,以求出最优路径
backpointer = torch.zeros(self.N, seq_len).long()
# self.Pi[i] 表示第一个字的标记为i的概率
# Bt[word_id]表示字为word_id的时候,对应各个标记的概率
# self.A.t()[tag_id]表示各个状态转移到tag_id对应的概率
# 所以第一步为
start_wordid = word2id.get(word_list[0], None)
Bt = B.t()
if start_wordid is None:
# 如果字不再字典里,则假设状态的概率分布是均匀的
bt = torch.log(torch.ones(self.N) / self.N)
else:
bt = Bt[start_wordid]
viterbi[:, 0] = Pi + bt
backpointer[:, 0] = -1
# 递推公式:
# viterbi[tag_id, step] = max(viterbi[:, step-1]* self.A.t()[tag_id] * Bt[word])
# 其中word是step时刻对应的字
# 由上述递推公式求后续各步
for step in range(1, seq_len):
wordid = word2id.get(word_list[step], None)
# 处理字不在字典中的情况
# bt是在t时刻字为wordid时,状态的概率分布
if wordid is None:
# 如果字不再字典里,则假设状态的概率分布是均匀的
bt = torch.log(torch.ones(self.N) / self.N)
else:
bt = Bt[wordid] # 否则从观测概率矩阵中取bt
for tag_id in range(len(tag2id)):
max_prob, max_id = torch.max(
viterbi[:, step-1] + A[:, tag_id],
dim=0
)
viterbi[tag_id, step] = max_prob + bt[tag_id]
backpointer[tag_id, step] = max_id
# 终止, t=seq_len 即 viterbi[:, seq_len]中的最大概率,就是最优路径的概率
best_path_prob, best_path_pointer = torch.max(
viterbi[:, seq_len-1], dim=0
)
# 回溯,求最优路径
best_path_pointer = best_path_pointer.item()
best_path = [best_path_pointer]
for back_step in range(seq_len-1, 0, -1):
best_path_pointer = backpointer[best_path_pointer, back_step]
best_path_pointer = best_path_pointer.item()
best_path.append(best_path_pointer)
# 将tag_id组成的序列转化为tag
assert len(best_path) == len(word_list)
id2tag = dict((id_, tag) for tag, id_ in tag2id.items())
tag_list = [id2tag[id_] for id_ in reversed(best_path)]
return tag_list
训练及测试
# 训练HMM模型
train_word_lists, train_tag_lists = train_data
test_word_lists, test_tag_lists = test_data
hmm_model = HMM(len(tag2id), len(word2id))
hmm_model.train(train_word_lists,
train_tag_lists,
word2id,
tag2id)
save_model(hmm_model, "/content/drive/Shared drives/A/temp_file/hmm.pkl")
# 评估hmm模型
pred_tag_lists = hmm_model.test(test_word_lists,
word2id,
tag2id)
metrics = Metrics(test_tag_lists, pred_tag_lists, remove_O=remove_O)
metrics.report_scores()
metrics.report_confusion_matrix()
return pred_tag_lists
运行结果:
正在训练评估HMM模型...
precision recall f1-score support
E-TITLE 0.9514 0.9637 0.9575 772
O 0.9568 0.9177 0.9369 5190
B-TITLE 0.8811 0.8925 0.8867 772
B-CONT 0.9655 1.0000 0.9825 28
B-EDU 0.9000 0.9643 0.9310 112
M-NAME 0.9459 0.8537 0.8974 82
B-RACE 1.0000 0.9286 0.9630 14
E-RACE 1.0000 0.9286 0.9630 14
M-ORG 0.9002 0.9327 0.9162 4325
M-LOC 0.5833 0.3333 0.4242 21
B-ORG 0.8422 0.8879 0.8644 553
E-PRO 0.6512 0.8485 0.7368 33
E-LOC 0.5000 0.5000 0.5000 6
M-EDU 0.9348 0.9609 0.9477 179
M-CONT 0.9815 1.0000 0.9907 53
E-NAME 0.9000 0.8036 0.8491 112
B-LOC 0.3333 0.3333 0.3333 6
E-EDU 0.9167 0.9821 0.9483 112
M-TITLE 0.9038 0.8751 0.8892 1922
E-CONT 0.9655 1.0000 0.9825 28
B-PRO 0.5581 0.7273 0.6316 33
M-PRO 0.4490 0.6471 0.5301 68
B-NAME 0.9800 0.8750 0.9245 112
E-ORG 0.8262 0.8680 0.8466 553
avg/total 0.9149 0.9122 0.9130 15100
Confusion Matrix:
E-TITLE O B-TITLE B-CONT B-EDU M-NAME B-RACE E-RACE M-ORG M-LOC B-ORG E-PRO E-LOC M-EDU M-CONT E-NAME B-LOC E-EDU M-TITLE E-CONT B-PRO M-PRO B-NAME E-ORG
E-TITLE 744 6 0 0 0 0 0 0 15 0 4 0 0 0 0 0 0 1 2 0 0 0 0 0
O 26 4763 26 0 1 0 0 0 204 0 37 4 0 1 0 2 0 2 78 0 3 12 0 30
B-TITLE 1 20 689 0 2 0 0 0 23 0 6 0 0 0 0 0 0 0 28 0 2 0 0 1
B-CONT 0 0 0 28 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
B-EDU 0 0 0 0 108 0 0 0 1 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0
M-NAME 0 3 0 0 0 70 0 0 3 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0
B-RACE 0 1 0 0 0 0 13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
E-RACE 0 1 0 0 0 0 0 13 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
M-ORG 4 70 17 0 3 2 0 0 4034 5 38 7 3 1 1 2 0 3 53 1 10 25 1 42
M-LOC 0 4 0 0 0 0 0 0 7 7 0 0 0 0 0 0 1 0 0 0 0 0 0 2
B-ORG 0 28 6 1 0 0 0 0 23 0 491 0 0 0 0 0 3 0 0 0 0 0 1 0
E-PRO 0 0 0 0 1 0 0 0 0 0 0 28 0 1 0 0 0 1 0 0 0 0 0 2
E-LOC 0 2 0 0 0 0 0 0 1 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0
M-EDU 0 1 0 0 0 0 0 0 0 0 0 0 0 172 0 0 0 0 0 0 1 4 0 1
M-CONT 0 0 0 0 0 0 0 0 0 0 0 0 0 0 53 0 0 0 0 0 0 0 0 0
E-NAME 0 16 0 0 0 2 0 0 0 0 0 0 0 0 0 90 0 0 0 0 0 0 0 3
B-LOC 0 1 0 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 0 0
E-EDU 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 110 0 0 0 0 0 0
M-TITLE 6 44 35 0 2 0 0 0 115 0 3 3 0 4 0 0 0 3 1682 0 1 7 0 17
E-CONT 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 28 0 0 0 0
B-PRO 0 0 0 0 1 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 24 3 0 0
M-PRO 0 0 0 0 1 0 0 0 18 0 0 0 0 1 0 0 0 0 0 0 1 44 0 3
B-NAME 0 8 0 0 0 0 0 0 2 0 1 0 0 0 0 0 0 0 0 0 0 0 98 0
E-ORG 1 10 9 0 1 0 0 0 30 0 0 0 0 0 0 0 0 0 18 0 1 3 0 480
【参考】

