LSTM笔记
背景知识
- 长短期记忆(Long short-term memory, LSTM)是一种特殊的RNN,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。
- 在普通的RNN中,重复模块结构非常简单,例如只有一个tanh层。LSTM也有这种链状结构,不过其重复模块的结构不同。LSTM的重复模块中有4个神经网络层,并且他们之间的交互非常特别。
网络结构
LSTM的关键是元胞状态(Cell State),也就是下图中横穿整个元胞顶部的水平线:
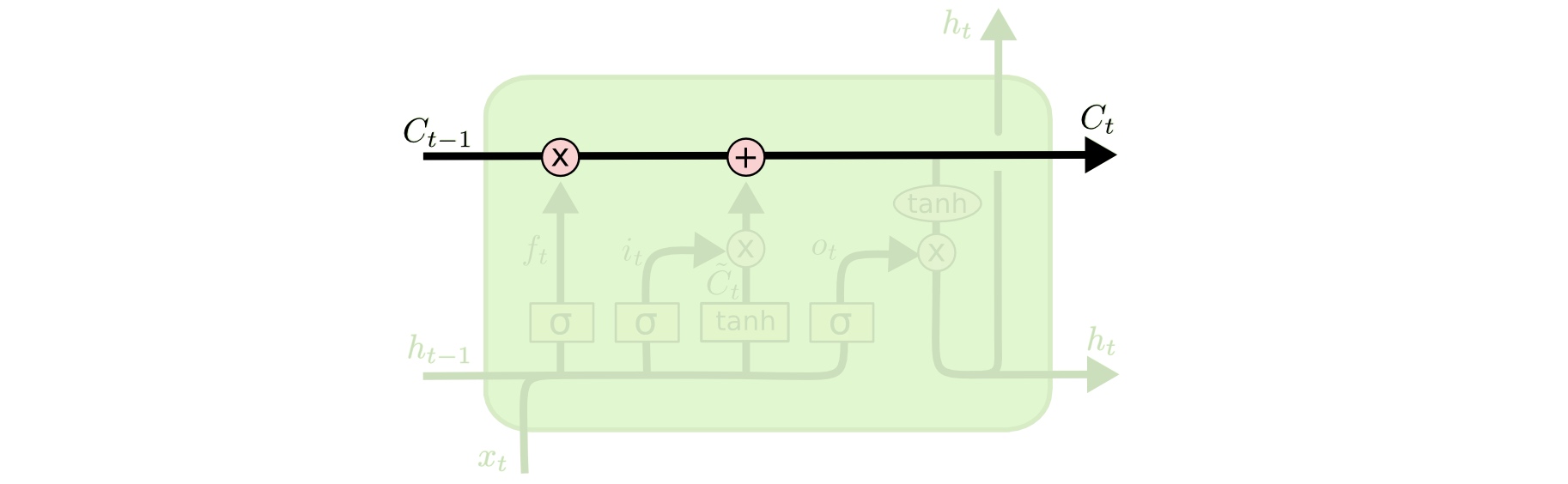
LSTM有能力对元胞状态添加或者删除信息,这种能力通过一种叫门的结构来控制。门是一种选择性让信息通过的方法。它们由一个Sigmoid函数和一个逐元素元素相乘的操作组成。
Sigmoid输出0~1之间的值,每个值表示对应的部分信息是否应该通过。0值表示不允许信息通过,1值表示让所有信息通过。一个LSTM有3个这种门,来保护和控制元胞状态。
遗忘门
遗忘门决定元胞状态将丢弃哪些信息,它的输入是\(h_{t-1}\)和\(x_t\)。来自先前隐藏状态的信息和来自当前输入的信息通过sigmoid函数传递。值介于0和1之间,越接近0意味着忘记,越接近1意味着要保持。
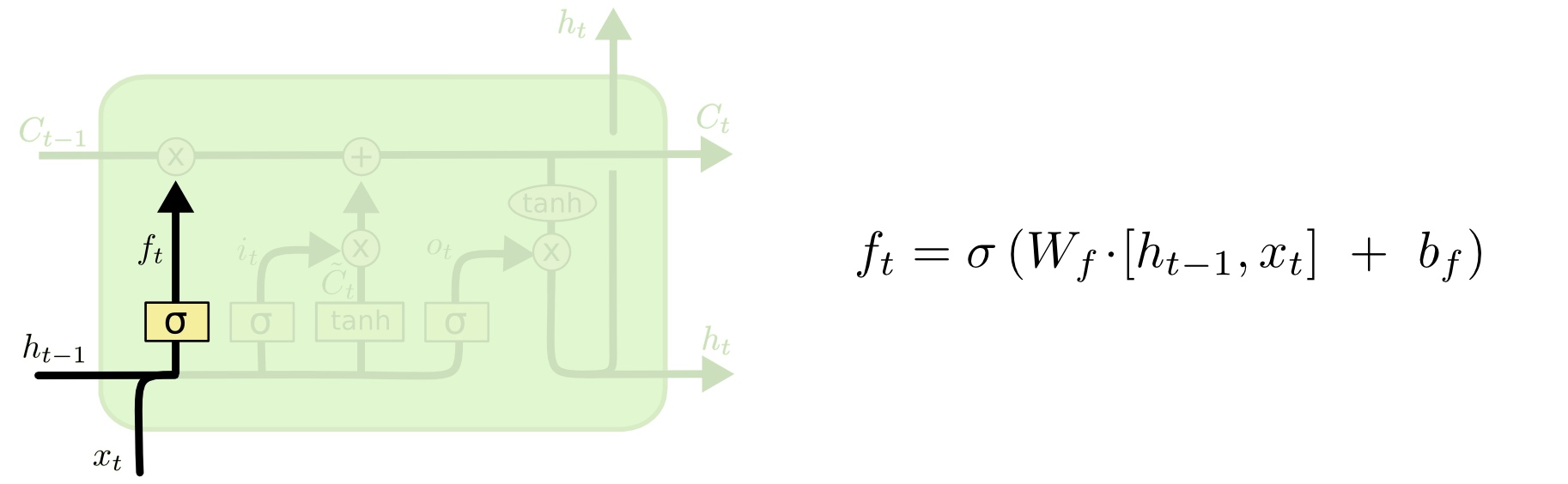
这里的\([h_{t-1},x_t]\)表示把两个向量连接成一个更长的向量
输入门
输入门决定哪些信息会进入到元胞状态中。首先,我们需要计算两个值:\(i_t\)和\(\tilde{C_t}\),它们的计算方法如图所示:
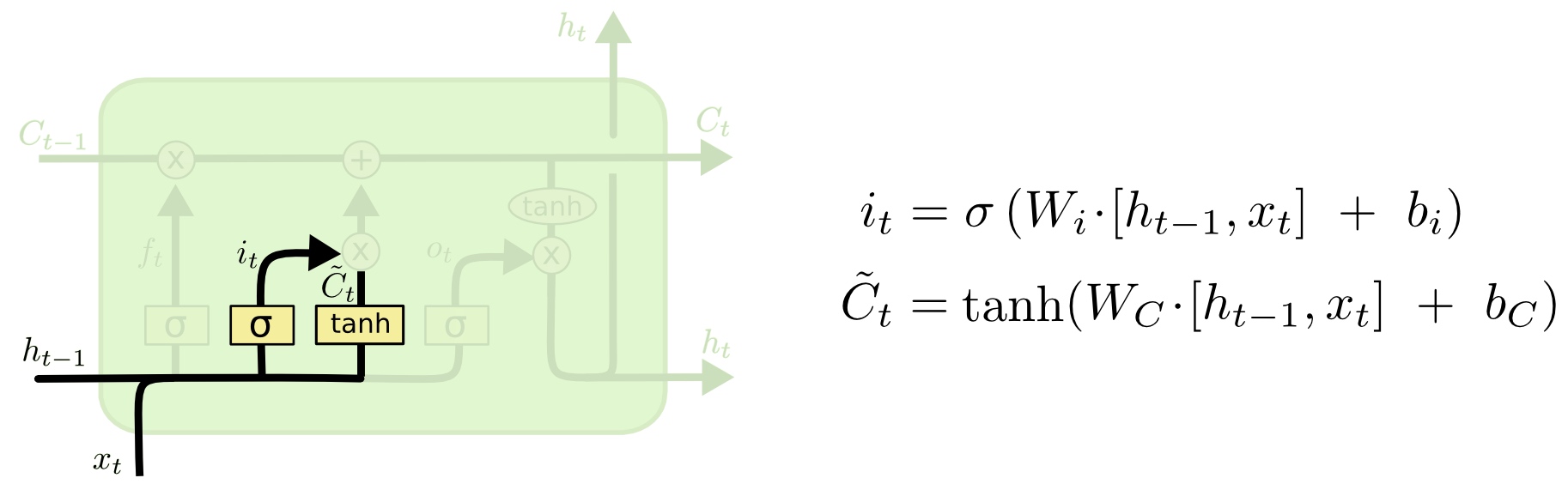
接下来,我们把旧状态\(C_{t-1}\)逐项乘以\(f_t\),忘掉我们已经决定忘记的内容。然后我们再加上\(i_t\bigodot\tilde{C_t}\)(这里\(\bigodot\)代表逐元素相乘),从而得到新的元胞状态\(C_t\):
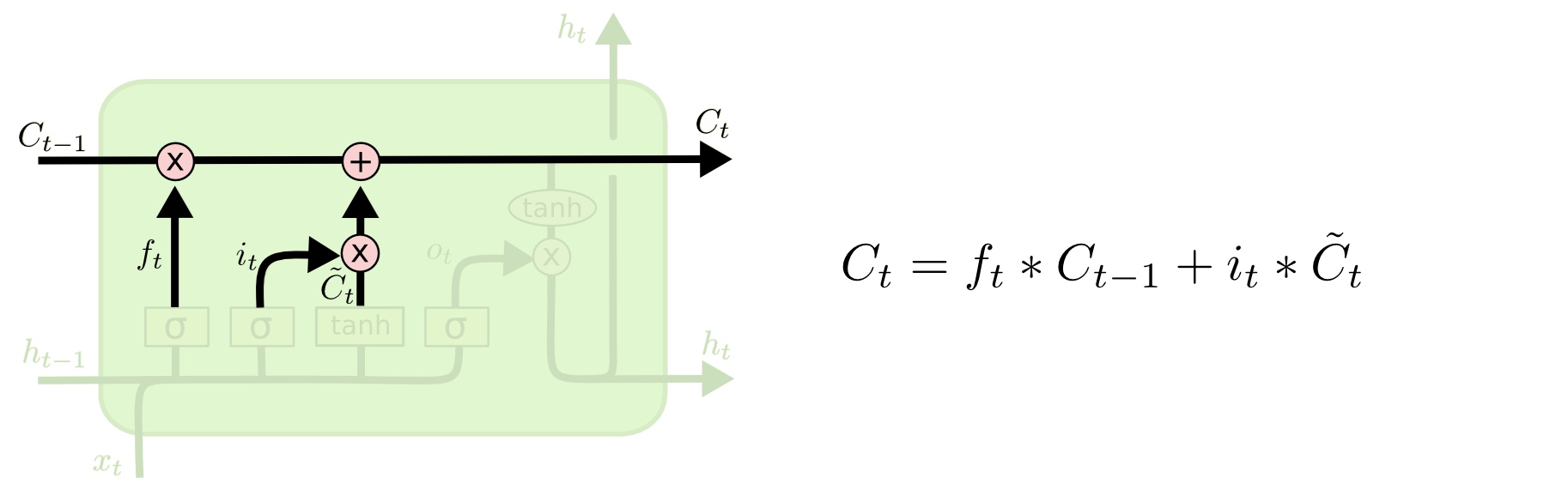
输出门
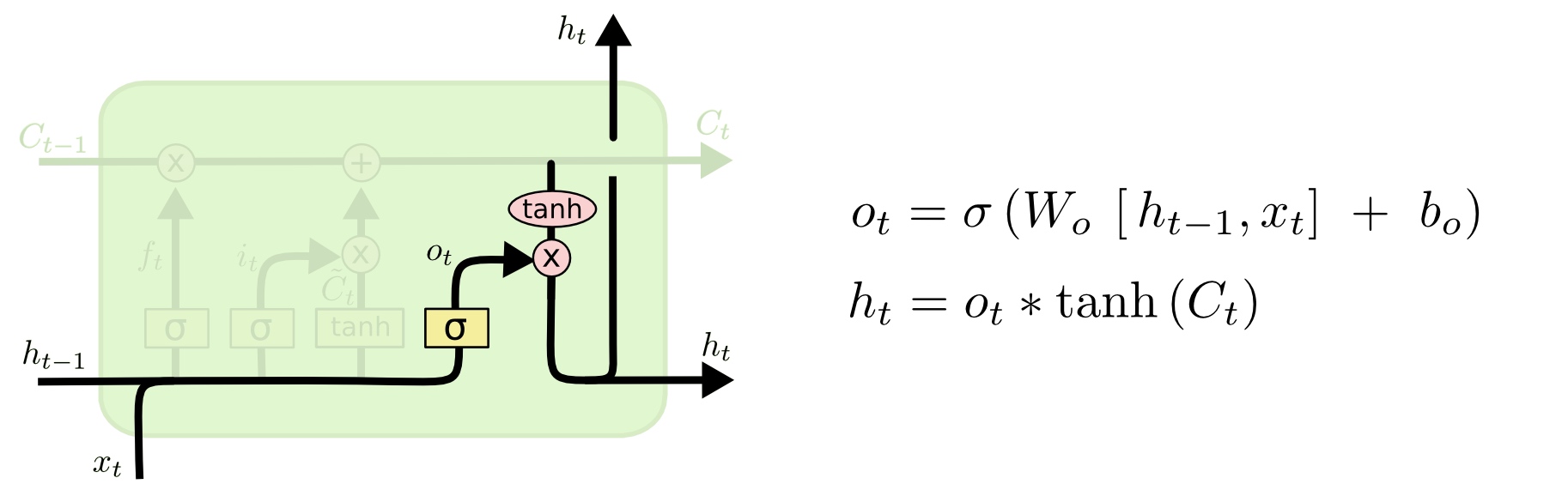
输出门计算网络的最终输出\(o_t\)以及网络继续运行所需的隐层单元\(h_t\),其计算方法如下:
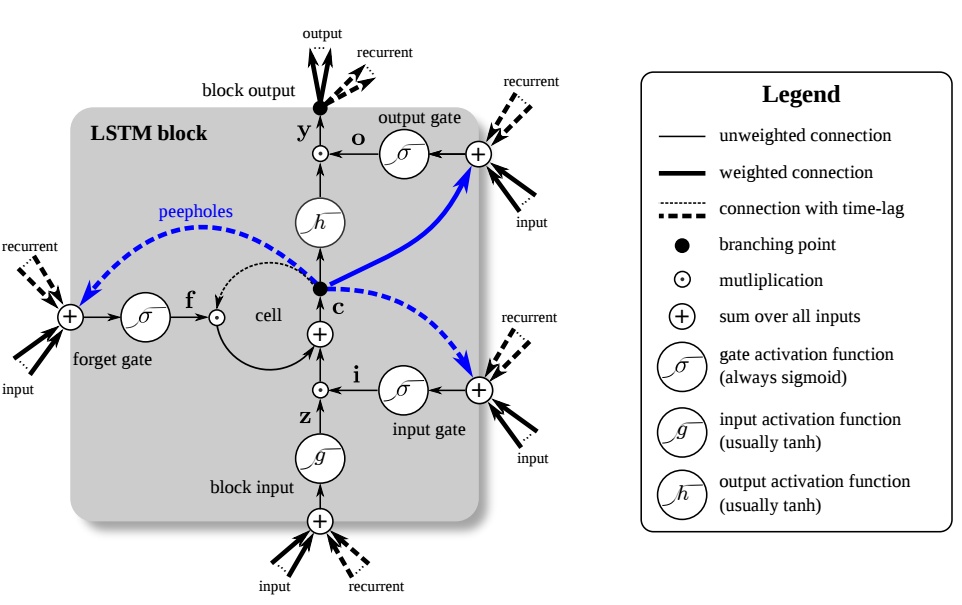
总结
用一张图来概况整个过程:
参考:


