CNN笔记
卷积
- 连续定义:\((f*g)(n)=\int_{-\infty }^{\infty }f(\tau)g(n-\tau)d\tau\)
- 离散定义:\((f*g)(n)=\sum_{\tau=-\infty }^{\infty }f(\tau)g(n-\tau)\)
- 通俗理解:所谓两个函数的卷积,本质上就是先将一个函数翻转,然后进行滑动叠加
- 在连续情况下,叠加指的是对两个函数的乘积求积分,在离散情况下就是加权求和
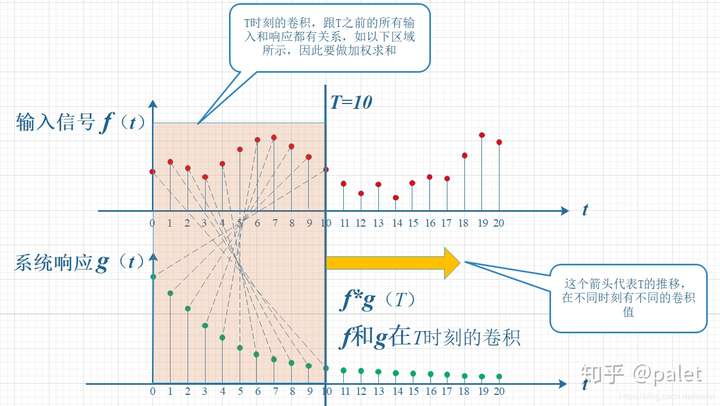
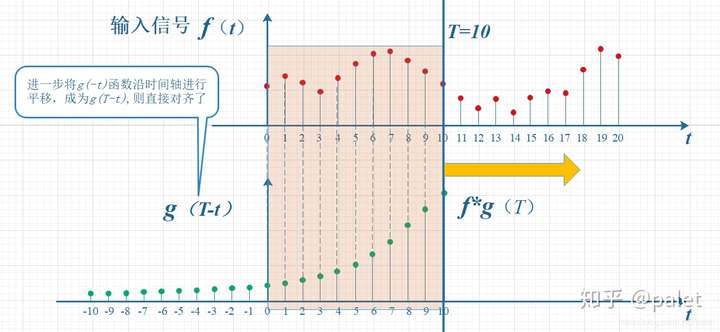
- 在连续情况下,叠加指的是对两个函数的乘积求积分,在离散情况下就是加权求和
卷积神经网络
意义
- 全连接DNN提取了过多无用的信息,我们可以考虑将它们删去
- CNN可以更高效地响应图像的局部特征
- 避免大量的参数导致网络迅速过拟合
- 卷积神经网络,正是由于卷积操作而得名。它进一步减少了参数,并且具有一定的平移、旋转、拉伸不变性
特点
卷积神经网络具有三个重要特点:
- local receptive fields(局部感受野)
- shared wights(共享权重)
- pooling(池化)
local receptive fields通过卷积操作来实现,它使得CNN可以更高效地捕捉局部区域下的特征:
shared wights指的是一个卷积层只使用一组权重(卷积核)。即:CN通过把单个卷积核在整幅图像上进行滑动来完成一组卷积层的映射:
池化
- 作用:过滤卷积操作中提取到的重复特征
- 两种最常用的池化方式:最大池化和均值池化
- 最大池化:取目标矩阵的最大值
- 均值池化:取目标矩阵的平均值
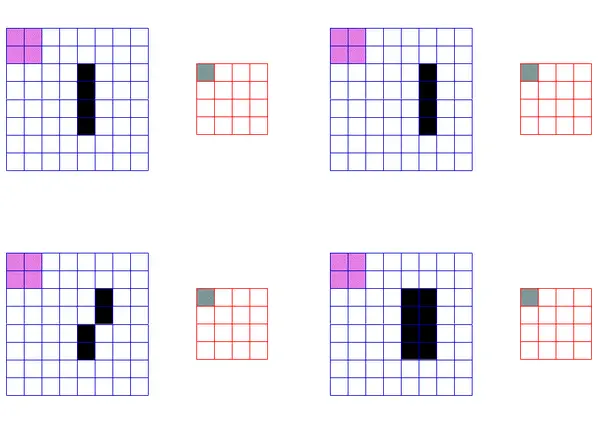
- 池化操作可以在一定程度上保持特征的平移、旋转和拉伸不变性,以最大池化为例:
卷积核(filter)
- 深度,高度,宽度
- 因为输入值有可能是多个向量(比如彩色图像的三通道数据),所以卷积核也要同时对多个向量进行卷积操作,这被形象地称为卷积核的“深度”
- 注意:不同深度的卷积核不共享权重
- 步长(stride)
- stride就是卷积过程中,卷积核每次滑动的步长
- 填充值(padding)
- padding简单来说就是在图像矩阵的边缘补0
- padding有一个良好性质,即可以控制输出数据体的空间尺寸(最常用的是用来保持输入数据体在空间上的尺寸,使得输入和输出的宽高都相等
- 详见:cnn卷积中padding的作用
输出数据体在空间上的尺寸 \(W_2\times H_2\times D_2\) 可以通过输入数据体尺寸 \(W_1\times H_1\times D_1\),卷积层中神经元的感受野尺寸(F),步长(S),卷积核数量(K)和零填充的数量(P)计算输出出来:
一般说来,当步长S=1时,零填充的值是P=(F-1)/2,这样就能保证输入和输出数据体有相同的空间尺寸
LeNet5

LeNet5是一个经典的卷积神经网络,这里引用pytorch tutorial中的实现:
import torch
import torchvision
import torchvision.transforms as transforms
# 准备数据
"""
torchvision.transforms.Compose(transforms)用于将多个transform组合起来使用,其参数是由transform构成的列表
class torchvision.transforms.Normalize(mean, std)用于将Tensor正则化:Normalized_image=(image-mean)/std
注意mean和std的维数要与数据的通道数一致
"""
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
# 定义网络
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5) # https://pytorch.org/docs/stable/nn.html#conv2d
self.pool = nn.MaxPool2d(2, 2) # https://pytorch.org/docs/stable/nn.html#maxpool2d
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120) # https://pytorch.org/docs/stable/nn.html#linear
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
# 定义损失函数和优化方法
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
# 利用GPU训练模型
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
net = net.to(device)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data[0].to(device), data[1].to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
# 测试模型
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
参考:


