DNN基础
复习一下深度学习的基础,重点关注反向传播过程
网络结构及符号说明
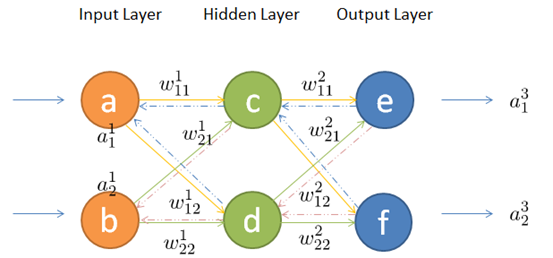

前向传播
节点c的输入:$z^2_1 = a^1_1 \cdot w^1_{11} + a^1_2 \cdot w^1_{21} + b^2_1 $
节点d同理,两个节点统一起来可用矩阵相乘来表示上述过程:
\(Z^2=W^1 \cdot A^1 + B^2\)
通过激活函数后,得到隐含层节点的输出:
\(A^2 = Activat(Z^2)\)
这里的\(Activat()\)代表激活函数,常见的激活函数包括: ReLU, sigmoid等等
反向传播
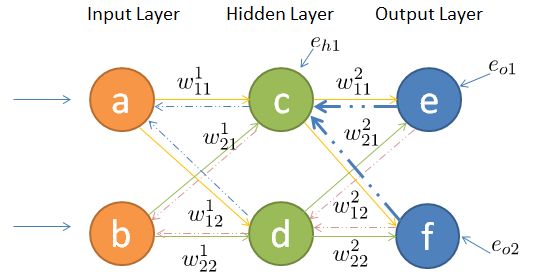
误差的反向传播
上图中\(e_{01}, e_{02}\)代表输出节点测得的误差
隐藏层节点c的误差为:
$ e_{h1}=\frac{w2_{11}}{w2_{11}+w^2_{21}}\cdot e_{01} + \frac{w2_{21}}{w2_{11}+w^2_{21}}\cdot e_{02}$
节点d的误差同理,综合起来可以写成矩阵相乘的形式:
\(\begin{bmatrix}e_{h1}\\ e_{h2}\end{bmatrix} = \begin{bmatrix} \frac{w^2_{11}}{w^2_{11}+w^2_{21}} & \frac{w^2_{12}}{w^2_{12}+w^2_{22}}\\ \frac{w^2_{21}}{w^2_{11}+w^2_{21}} & \frac{w^2_{22}}{w^2_{12}+w^2_{22}} \end{bmatrix} \cdot \begin{bmatrix}e_{01}\\ e_{02}\end{bmatrix}\)
在计算时,可以把分母提出来去掉,保持结果的比例不变,即:
\(\begin{bmatrix}e_{h1}\\ e_{h2}\end{bmatrix} =
\begin{bmatrix}
w^2_{11} & w^2_{12}\\
w^2_{21} & w^2_{22}
\end{bmatrix} \cdot \begin{bmatrix}e_{01}\\ e_{02}\end{bmatrix}\)
可见,此时的权重矩阵恰好等于上文中前向传播时权重矩阵的转置,故有:
\(E_h = W^T \cdot E_0\)
链式求导
以下图为例:
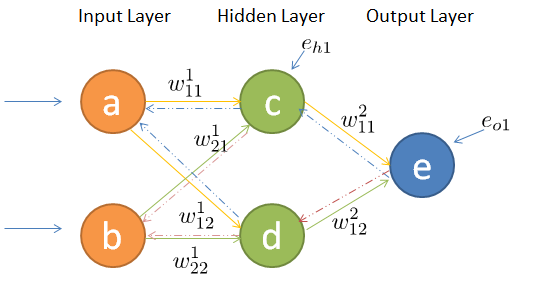
假设损失函数为:\(f_{loss}() = \frac{1}{2}(\hat y - y)^2\),
激活函数为:\(f_{active}() = sigmoid(x)\)
那么,如何对\(w^1_{11}\)进行更新呢?我们先来考虑节点c,已知:
\(e_{01} = \frac{1}{2}(a^3-y_1)^2\)
\(a^3 =sigmoid(z^3)\)
\(z^3 = w^2_{11}\cdot a^2_1 + w^2_{12}\cdot a^2_2 + b^3\)
这里\(y_1\)代表样本\(x_1\)对应的真实结果,\(a^3\)代表神经网络对样本\(x_1\)对应的预测结果。根据链式法则,误差对\(w^2_{11}\)求偏导如下:
\(\frac{\partial e_{01}}{\partial w^2_{11}} = \frac{\partial e_{01}}{\partial a^3} \cdot \frac{\partial a^3}{\partial z^3} \cdot \frac{\partial z^3}{\partial w^2_{11}}\)
代入前三个式子,算得(所有值已知):
\(\frac{\partial e_{01}}{\partial w^2_{11}} = (a^3 - y_1) \cdot sigmoid(z^3) \cdot (1-sigmoid(z^3)) \cdot a^2_1\)
同理,误差对\(w^2_{12}\)的偏导如下:
\(\frac{\partial e_{01}}{\partial w^2_{12}} = \frac{\partial e_{01}}{\partial a^3} \cdot \frac{\partial a^3}{\partial z^3} \cdot \frac{\partial z^3}{\partial w^2_{12}}\)
计算后得到:
\(\frac{\partial e_{01}}{\partial w^2_{11}} = (a^3 - y_1) \cdot sigmoid(z^3) \cdot (1-sigmoid(z^3)) \cdot a^2_2\)
同理,误差对偏置\(b^3\)求偏导如下:
\(\frac{\partial e_{01}}{\partial w^2_{12}} = \frac{\partial e_{01}}{\partial a^3} \cdot \frac{\partial a^3}{\partial z^3} \cdot \frac{\partial z^3}{\partial b^3}\)
计算后得:
\(\frac{\partial e_{01}}{\partial w^2_{11}} = (a^3 - y_1) \cdot sigmoid(z^3) \cdot (1-sigmoid(z^3))\)
接下来,再往前走一层,已知:
\(a^2_1 = sigmoid(z^2_1)\)
\(z^2_1 = w^1_{11}\cdot a^1_1 + w^1_{12}\cdot a^1_2 + b^2_1\)
因此误差对输入层的\(w^1_{11}\)求偏导如下:
\(\frac{\partial e_{01}}{\partial w^2_{11}} = \frac{\partial e_{01}}{\partial a^3} \cdot \frac{\partial a^3}{\partial z^3} \cdot \frac{\partial z^3}{\partial w^2_{11}} \cdot \frac{\partial a^2_1}{\partial z^2_1} \cdot \frac{\partial z^2_1}{\partial w^1_{11}}\)
其中,前三个乘数是由隐藏层与输出层涉及到的三个式子推出的,后两个乘数是由刚刚引入的两个式子得到的
最后算得:
...太长了不写了= =,计算方法与前面写的类似,再求个导就好了
同理,输入层的其他三个参数按照同样的方法即可求出各自的偏导,在这不再赘述。
在每个参数偏导数明确的情况下,带入梯度下降公式即可:
\(w = w - \eta\frac{\partial e}{\partial w}\)
\(b = b - \eta\frac{\partial e}{\partial b}\)
引入delta
在上述过程中,我们可以发现:在使用链式法则对参数进行更新时,涉及到了很多重复计算。因此,我们可以把已经计算完毕的节点的偏导数保存为中间变量,以供后续的计算使用。

上图中红色的部分就是公式中相同的部分,我们可以将其抽象出来作为\(\delta\)
经典书籍《神经网络与深度学习》中对于delta的描述为在第l层第j个神经元上的误差,定义为误差对于当前带权输入求偏导,数学公式如下:
$\delta^l_j \equiv \frac{\partial C}{\partial z^l_j} $
这里的\(C\)代表模型的预测误差
举个例子,前面算过的输出层的误差可以表示为:
\(\begin{align*} \delta ^3_1 = \frac{\partial e_{01}}{\partial b^3} &= (a^3_1 - y_1) \cdot sigmoid(z^3_1) \cdot (1-sigmoid(z^3))\\ &= [(a^3_1 - y_1)] \cdot [sigmoid(z^3_1) \cdot (1-sigmoid(z^3))]\\ &= \bigtriangledown _a C \odot {\sigma}'(z^3_1) \end{align*}\)
结合前面的式子可以看出:
\(\bigtriangledown _a C = \frac{\partial e_{01}}{\partial a^3} = a^3_1 - y_1\)
同理,隐藏层的误差可以表示为:

权重更新可表示为:

偏置更新可表示为:
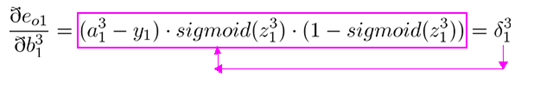
综合后,我们就得到了《神经网络与深度学习》书中反向传播4大公式(详细推导证明可移步此书):
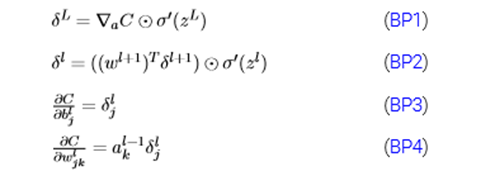
其中,BP1与BP2相结合可以计算出任意层的误差:只要首先利用BP1公式计算出输出层误差,然后利用BP2层层传递就行了。同时,对于权重w以及偏置b我们可以通过BP3和BP4公式来计算。
参考:


