推荐算法之矩阵分解

翻到了以前总结的SVD笔记，正好借此机会复习一下

奇异值分解

方阵的特征分解:

Ax=λx, 其中A为一个n×n的矩阵, λ为特征值, x为λ所对应的特征向量

对于矩阵A的n个特征值λ1≤λ2≤...≤λn, 以及这n个特征值所对应的特征向量{x1,x2,...xn}

矩阵A可作如下分解: \(A=WΣW^{-1}\), 其中W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵

奇异值分解:

奇异值分解不要求矩阵为方阵:

假设矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

\[A=UΣV^T \]

其中U是一个m×m的矩阵, V是一个n×n的矩阵, 它们除了主对角线上的元素以外全为0,且都满足:

\[U^TU=I,V^TV=I \]

其中矩阵V是方阵\(A^TA\)的n个特征向量所张成的n×n矩阵, 我们把这里用到的特征向量称做矩阵A的右奇异向量

矩阵U是方阵\(AA^T\)的m个特征向量所张成的m×m矩阵, 这里的特征向量称为矩阵A的左奇异向量

矩阵\(Σ\)除了对角线上是奇异值,其他位置都是0

奇异值\(σ_i = Av_i / u_i\), 其中vi和ui分别是A的右, 左奇异向量

同样, 奇异值还可以通过\(σ_i = \sqrt{λ_i}\)求得, 其中λ为\(A^TA\)和\(AA^T\)的特征值(两个矩阵的特征值是一样的)

SVD的性质:

我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵:

\[A_{m×n}=U_{m×m}Σ_{m×n}V^T_{n×n}≈U_{m×k}Σ_{k×k}V^T_{k×n} \]

---

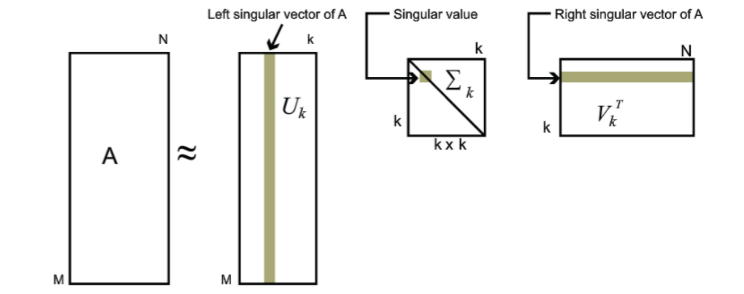
SVD在推荐系统中的应用

用户特征: 一组实向量, 描述了用户对具备属性a,b,c,...的电影的偏好程度 user(Xa, Xb, Xc,...)

电影特征: 一组实向量, 描述了电影队属性a,b,c,...的符合程度 movie(Xa, Xb,Xc,...)

用户对电影的评分预测值, 就是上述两个向量的内积[1]

将m个用户和n个物品对应的评分看做一个矩阵M[3], 对这个m×n矩阵进行SVD分解:

\[M_{m×n}=U_{m×k}Σ_{k×k}V^T_{k×n} \]

如果我们要预测第i个用户对第j个物品的评分\(m_{ij}\),则只需要计算\(u^T_iΣv_j\)即可

问题:

1. SVD分解要求矩阵M是稠密的,而实际数据中矩阵M是稀疏的
2. 实际数据中矩阵M非常庞大,做分解非常耗时

---

FunkSVD

FunkSVD的提出是为了解决传统SVD的效率问题, 其期望的矩阵分解方式为:

\[M_{m×n}=P^T_{m×k}Q_{k×n} \]

对于某一个用户评分\(m_{ij}\),如果用FunkSVD进行矩阵分解，则对应的表示为\(q^T_jp_i\)，采用均方差做为损失函数，则我们期望\((m_{ij}−q^T_jp_i)^2\)尽可能的小，如果考虑所有的物品和样本的组合，则我们期望最小化下式：

\[∑_{i,j}(m_{ij}−q^T_jp_i)^2 \]

为了防止过拟合，加入一个L2的正则化项, 就得到了最终的目标函数:

\[J(p,q) = \underbrace{arg\;min}_{p_i,q_j}\;\sum\limits_{i,j}(m_{ij}-q_j^Tp_i)^2 + \lambda(||p_i||_2^2 + ||q_j||_2^2 ) \]

其中λ为正则化系数，需要调参。arg minf(x)是指使得函数f(x)取得其最小值的所有自变量 x 的集合。

---

BIgChaos

消除Global Effect

相似度矩阵分解

除此之外，SVD还有很多其他的改进类型，包括Hestenes SVD，SVD++等等，时间所限，暂时先不展开了。不过网上相关的Blog和文献也有很多，有兴趣的同学可以自己找资料学习一下

参考资料

[1] 王元涛. Netflix数据集上的协同过滤算法[D]. 清华大学, 2009.

[2] 奇异值分解(SVD)原理与在降维中的应用 - 刘建平Pinard

[3] 矩阵分解在协同过滤推荐算法中的应用 - 刘建平Pinard

[4] 正则化为什么能防止过拟合

[5] 机器学习中使用正则化来防止过拟合是什么原理？ - 邓子明的回答 - 知乎