bzoj 3612: [Heoi2014]平衡【整数划分dp】

其实就是-n~n中求选k个不同的数，和为0的方案数
学到了新姿势叫整数划分，具体实现是dp 详见：https://blog.csdn.net/Vmurder/article/details/42551603
设f[i][j]为j个数和为i的方案数，然后因为互不相同，所以转移的话有两种，就是当前j个数全部+1，和当前j个数全部+1并且多填一个1出来，也就是f[i][j]=f[i-j][j]+f[i-j][j-1]
但是这里要求选的数不能超过n，我们考虑i>n的f中一定有一个大于n的数，我们把这种情况减掉就行了，也就是f[i][j]-=f[i-n-1][j-1]

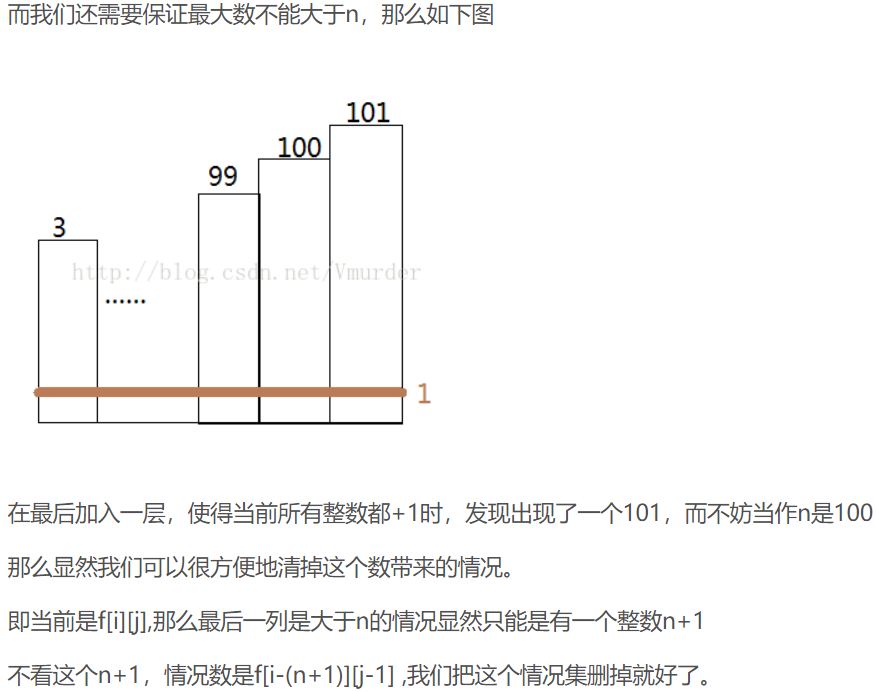
这是上面那个blog的截图

#include<iostream>
#include<cstdio>
using namespace std;
const int N=100005;
int T,n,m,mod,f[N][15],ans;
int read()
{
	int r=0,f=1;
	char p=getchar();
	while(p>'9'||p<'0')
	{
		if(p=='-')
			f=-1;
		p=getchar();
	}
	while(p>='0'&&p<='9')
	{
		r=r*10+p-48;
		p=getchar();
	}
	return r*f;
}
int main()
{
	T=read();
	while(T--)
	{
		n=read(),m=read(),mod=read();
		f[0][0]=1,ans=0;
		for(int i=1;i<=n*m;i++)
			for(int j=1;j<=m;j++)
			{
				if(i>=j)
					f[i][j]=(f[i-j][j]+f[i-j][j-1])%mod;
				if(i>n)
					f[i][j]=(f[i][j]-f[i-n-1][j-1]+mod)%mod;
			}
		for(int i=1;i<=n*m;i++)
			for(int j=1;j<=m;j++)
			{
				ans=(ans+f[i][j]*f[i][m-j])%mod;
				if(j!=m)
					ans=(ans+f[i][j]*f[i][m-j-1])%mod;
			}
		printf("%d\n",ans+(m==1));
	}
	return 0;
}