bzoj 1576: [Usaco2009 Jan]安全路经Travel【spfa+树链剖分+线段树】
这几天写USACO水题脑子锈住了……上来就贪心,一交就WA
事实上这个是一个叫最短路树的东西,因为能保证只有一条最短路,所以所有最短路合起来是一棵以1为根的树,并且在这棵树上,每个点被精灵占据的路是它通向father的
先spfa把最短路dis[]和最短路树求出来,把被选入最短路树的边打上删除标记
把这棵树树剖了,放在线段树上维护最小值
然后看没有被删除的边(u,v,w),,设它在树上是这样的:
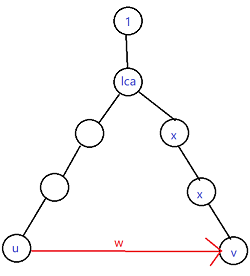
然后现在考虑这条边的贡献,观察两个x点和v点(方便起见已下把v点也归入x)。如果删掉其到father的路,从1可以走1→lca→u→v→x,所以这条(u,v,w)能给从lca(不包含lca)到v路径上的点x贡献一条长度为disu+w(u→v)+(dis[v]-dis[x])(v→x)的路径。因为要求最短路,所以-dis[x]固定,要求min(dis[u]+dis[v]+w),直接在线段树上更新这些点的这个值即可
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N=100005,M=400005,inf=2e9+7;
int n,m,h[N],cnt,dis[N],x[M],y[M],z[M],bl[N];
int fa[N],de[N],hs[N],si[N],fr[N],id[N],rl[N],tmp;
bool v[N],mk[M];
struct qwe
{
int ne,to,va;
}e[M];
struct xds
{
int l,r,mn,lz;
}t[N<<2];
int read()
{
int r=0,f=1;
char p=getchar();
while(p>'9'||p<'0')
{
if(p=='-')
f=-1;
p=getchar();
}
while(p>='0'&&p<='9')
{
r=r*10+p-48;
p=getchar();
}
return r*f;
}
void add(int u,int v,int w)
{//if(!w)cerr<<u<<" "<<v<<endl;
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
e[cnt].va=w;
h[u]=cnt;
x[cnt]=u,y[cnt]=v,z[cnt]=w;
}
void jia(int u,int v)
{
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
h[u]=cnt;
}
void dfs1(int u,int fat)
{
si[u]=1;
de[u]=de[fat]+1;
for(int i=h[u];i;i=e[i].ne)
if(e[i].to!=fat)
{
dfs1(e[i].to,u);
si[u]+=si[e[i].to];
if(si[hs[u]]<si[e[i].to])
hs[u]=e[i].to;
}
}
void dfs2(int u,int top)
{
fr[u]=top;
id[u]=++tmp;
rl[tmp]=u;
if(!hs[u])
return;
dfs2(hs[u],top);
for(int i=h[u];i;i=e[i].ne)
if(e[i].to!=hs[u]&&e[i].to!=fa[u])
dfs2(e[i].to,e[i].to);
}
int lca(int u,int v)
{
for(;fr[u]!=fr[v];de[fr[u]]>de[fr[v]]?u=fa[fr[u]]:v=fa[fr[v]]);
return de[u]<de[v]?u:v;
}
void pd(int ro)
{
if(t[ro].lz!=inf)
{
t[ro<<1].mn=min(t[ro<<1].mn,t[ro].lz);
t[ro<<1].lz=min(t[ro<<1].lz,t[ro].lz);
t[ro<<1|1].mn=min(t[ro<<1|1].mn,t[ro].lz);
t[ro<<1|1].lz=min(t[ro<<1|1].lz,t[ro].lz);
t[ro].lz=inf;
}
}
void build(int ro,int l,int r)
{
t[ro].l=l,t[ro].r=r,t[ro].mn=t[ro].lz=inf;
if(l==r)
return;
int mid=(l+r)>>1;
build(ro<<1,l,mid);
build(ro<<1|1,mid+1,r);
}
void update(int ro,int l,int r,int w)
{//cerr<<t[ro].l<<" "<<t[ro].r<<" "<<l<<" "<<r<<endl;
if(t[ro].l==l&&t[ro].r==r)
{
t[ro].mn=min(t[ro].mn,w);
t[ro].lz=min(t[ro].lz,w);
return;
}
pd(ro);
int mid=(t[ro].l+t[ro].r)>>1;
if(r<=mid)
update(ro<<1,l,r,w);
else if(l>mid)
update(ro<<1|1,l,r,w);
else
update(ro<<1,l,mid,w),update(ro<<1|1,mid+1,r,w);
t[ro].mn=min(t[ro<<1].mn,t[ro<<1|1].mn);
}
void gai(int u,int v,int w)
{//cerr<<u<<" "<<v<<endl;
while(fr[u]!=fr[v])
{
if(de[fr[u]]<de[fr[v]])
swap(u,v);
update(1,id[fr[u]],id[u],w);
u=fa[fr[u]];
}
if(u!=v)
{
if(de[u]>de[v])
swap(u,v);
update(1,id[u]+1,id[v],w);
}
}
int ques(int ro,int p)
{
if(t[ro].l==t[ro].r)
return t[ro].mn;
pd(ro);
int mid=(t[ro].l+t[ro].r)>>1;
if(p<=mid)
return ques(ro<<1,p);
else
return ques(ro<<1|1,p);
}
int main()
{
n=read(),m=read();
for(int i=1;i<=m;i++)
{
int x=read(),y=read(),z=read();
add(x,y,z),add(y,x,z);
}
for(int i=1;i<=n;i++)
dis[i]=inf;
deque<int>q;
v[1]=1,dis[1]=0,q.push_back(1);
while(!q.empty())
{
int u=q.front();
q.pop_front();
v[u]=0;
for(int i=h[u];i;i=e[i].ne)
if(dis[e[i].to]>dis[u]+e[i].va)
{
dis[e[i].to]=dis[u]+e[i].va;
fa[e[i].to]=u,bl[e[i].to]=i;
if(!v[e[i].to])
{
v[e[i].to]=1;
if(q.empty()||dis[e[i].to]>dis[q.front()])
q.push_back(e[i].to);
else
q.push_front(e[i].to);
}
}
}
memset(h,0,sizeof(h));
cnt=0;
for(int i=2;i<=n;i++)
{
jia(fa[i],i),jia(i,fa[i]);
mk[bl[i]]=1;
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
for(int i=1;i<=2*m;i++)
if(!mk[i])
gai(lca(x[i],y[i]),y[i],dis[x[i]]+dis[y[i]]+z[i]);//,cerr<<x[i]<<" "<<y[i]<<" "<<z[i]<<endl;//cerr<<"ok"<<endl;
for(int i=2;i<=n;i++)
{
int ans=ques(1,id[i]);
printf("%d\n",ans==inf?-1:ans-dis[i]);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号