bzoj 1565 [NOI2009]植物大战僵尸【tarjan+最大权闭合子图】
一上来以为是裸的最大权闭合子图,上来就dinic
…然后没过样例。不得不说样例还是非常良心的给了一个强连通分量,要不然就WA的生活不能自理了
然后注意到有一种特殊情况:每个植物向他保护的植物连边(包括被其挡在后面的),当植物的保护范围连成一个强连通分量时,这个强连通分量上的植物以及从这个强连通分量连出去的植物,都不会在任何情况下被攻击
如下图:
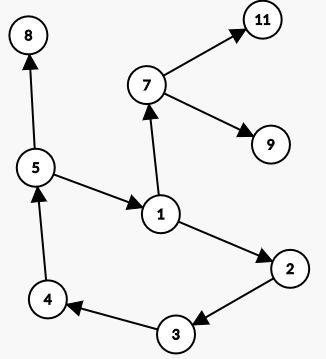
12345所形成的强连通分量不会被攻击,所以它所延伸出来的植物也不会被攻击,即图上所有点都不会被攻击
对于这种情况,用tarjan缩点,对于每个缩后的点记录一个size,对于所有 \(size[belong[u]]>1\) 的点向外dfs,记录不会被攻击到的点即可
删去所有不会被攻击到的点及其所连的边之后,跑最大权闭合子图。
具体如下:
- s点向所有正权点连边,流量为点权;所有负权点向t连边,流量为负点权(即正数!)
- 对于所有有依赖关系的点,由被保护的植物向保护植物连边(也就是把上面为tarjan建的图所有有向边反过来),也就是最大权闭合子图中的向其依赖点连边,流量为inf
\[ans=\sum 正权点点权-最小割
\]
- 割的意义:与原点相连的点表示被选择,与汇点相连的点表示不选
- S连向正权点的边被割:说明正权点被划入T侧,代表不选,收益被扣除
- 负权点连向T的边被割:说明负权点被划入S侧,代表被选,要承受惩罚
- 有依赖关系的点之间无法被割:a-->b,则如果a在S侧那b也一定在S侧
莫名跑的慢,大概是写丑了
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<vector>
using namespace std;
const int E=1000005,inf=1e9,N=55,P=1005;
int n,m,sum,h[E],cnt,le[E],s,t,v[N][N],dfn[P],tot,low[P],st[P],top,con,bl[P],si[P];
bool in[P];
vector<pair<int,int> >vec;
struct qwe
{
int ne,to,va;
}e[E<<1];
int read()
{
int r=0,f=1;
char p=getchar();
while(p>'9'||p<'0')
{
if(p=='-')
f=-1;
p=getchar();
}
while(p>='0'&&p<='9')
{
r=r*10+p-48;
p=getchar();
}
return r*f;
}
void addd(int u,int v)
{//cout<<u<<" "<<v<<endl;
vec.push_back(make_pair(u,v));
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
h[u]=cnt;
}
void add(int u,int v,int w)
{
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
e[cnt].va=w;
h[u]=cnt;
}
void ins(int u,int v,int w)
{//cout<<u<<" "<<v<<" "<<w<<endl;
add(u,v,w);
add(v,u,0);
}
bool bfs()
{
queue<int>q;
memset(le,0,sizeof(le));
le[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];i;i=e[i].ne)
if(e[i].va>0&&!le[e[i].to])
{
le[e[i].to]=le[u]+1;
q.push(e[i].to);
}
}
return le[t];
}
int dfs(int u,int f)
{
if(u==t||!f)
return f;
int us=0;
for(int i=h[u];i&&us<f;i=e[i].ne)
if(le[e[i].to]==le[u]+1&&e[i].va>0)
{
int t=dfs(e[i].to,min(e[i].va,f-us));
e[i].va-=t;
e[i^1].va+=t;
us+=t;
}
if(!us)
le[u]=0;
return us;
}
int dinic()
{
int re=0;
while(bfs())
re+=dfs(s,inf);
return re;
}
void dfs(int u)
{
in[u]=1;
for(int i=h[u];i;i=e[i].ne)
if(!in[e[i].to])
dfs(e[i].to);
}
void tarjan(int u)
{//cout<<u<<endl;
dfn[u]=low[u]=++tot;
in[u]=1;
st[++top]=u;
for(int i=h[u];i;i=e[i].ne)
{
if(!dfn[e[i].to])
{
tarjan(e[i].to);
low[u]=min(low[u],low[e[i].to]);
}
else if(in[e[i].to])
low[u]=min(low[e[i].to],dfn[e[i].to]);
}
if(dfn[u]==low[u])
{
con++;
while(st[top]!=u)
{
in[st[top]]=0;
bl[st[top--]]=con;
si[con]++;
}
in[st[top]]=0;
bl[st[top--]]=con;
si[con]++;
}
}
int main()
{
n=read(),m=read();
t=n*m+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
v[i][j]=read();
int id=(i-1)*m+j,w=read(); //cout<<sor<<" "<<w<<endl;
if(j>1)
addd(id,id-1);
while(w--)
{
int x=read()+1,y=read()+1;
addd(id,(x-1)*m+y);
}
}//cout<<"ok"<<endl;
for(int i=1;i<=n*m;i++)
if(!dfn[i])
tarjan(i);//,cout<<i<<endl;
for(int i=1;i<=n*m;i++)
if(si[bl[i]]>1&&!in[i])
dfs(i);
cnt=1;
memset(h,0,sizeof(h));
memset(e,0,sizeof(e));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!in[(i-1)*m+j])
{
int x=(i-1)*m+j;
if(v[i][j]>=0)
ins(s,x,v[i][j]),sum+=v[i][j];
else
ins(x,t,-v[i][j]);
}
for(int i=0;i<vec.size();i++)
if(!in[vec[i].first]&&!in[vec[i].second])
ins(vec[i].second,vec[i].first,inf);//cout<<"ok"<<endl;
printf("%d\n",sum-dinic());
return 0;
}




