bzoj 2127 happiness【最小割+dinic】
参考:https://www.cnblogs.com/chenyushuo/p/5144957.html 不得不说这个建图方法真是非常妙啊
假设S点选理,T点选文,a[i][j]为(i,j)选文收益,b[i][j]为(i,j)选理收益,c[i][j]为同时选文收益,d[i][j]为同时选文收益。
那么对于每个点x=(i+1)*m+j,我们连接
\[c[s,x]=b[i][j]
\]
\[c[x,t]=a[i][j]
\]
对于有利益相关的x,y两点,连接
\[c[s,x]=d[i][j]/2
\]
\[c[s,y]=d[i][j]/2
\]
\[c[x,t]=c[i][j]/2
\]
\[c[y,t]=c[i][j]/2
\]
\[c[x,y]=c[i][j]/2+d[i][j]/2
\]
\[c[y,x]=c[i][j]/2+d[i][j]/2
\]
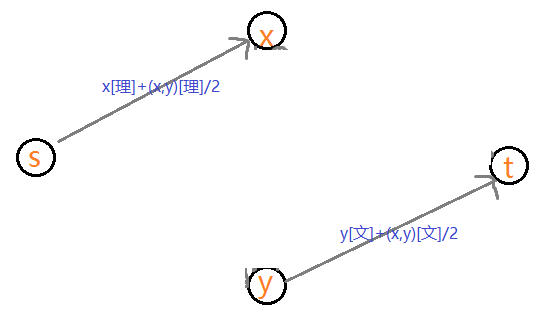
建完的图:
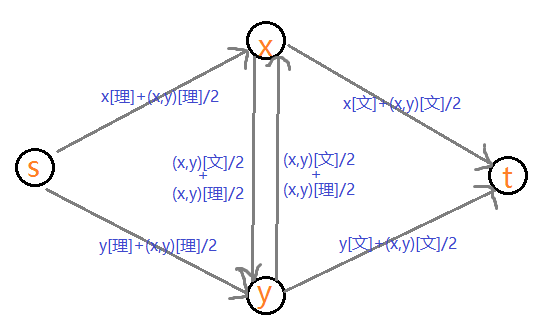
然后考虑最小割,下面枚举几种情况:
都选文,即割掉了x选理,y选理和(x,y)都选理:
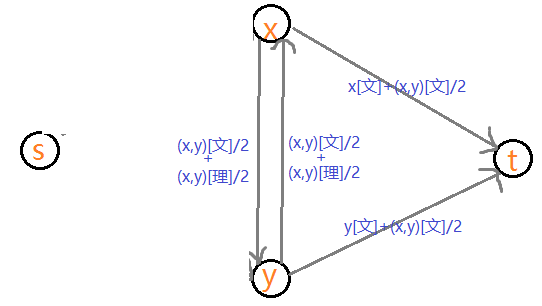
都选理,即割掉了x选文,y选文和(x,y)都选文:
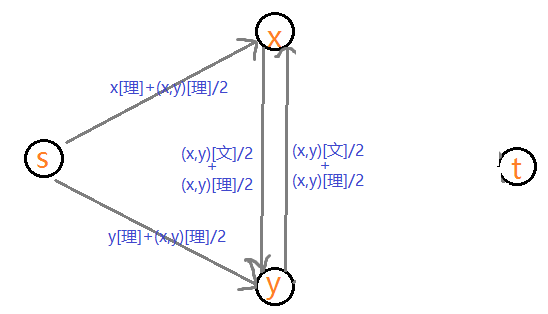
x选文y选理,即割掉了x选理,y选文,(x,y)都选理/+(x,y)都选理/2+(x,y)都选文/2+(x,y)都选文/2,即,割掉x选理,y选文,(x,y)都选理,(x,y)都选文:
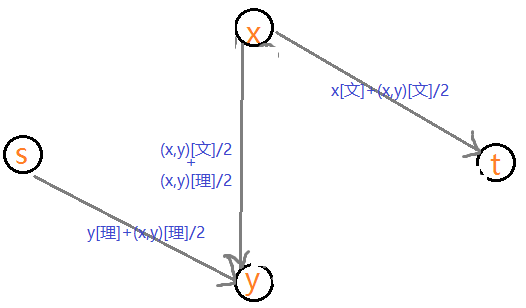
y选文x选理,即割掉了x选文,y选理,(x,y)都选理/+(x,y)都选理/2+(x,y)都选文/2+(x,y)都选文/2,即,割掉x选文,y选理,(x,y)都选理,(x,y)都选文:
对于除以2的操作,为避免下取整的误差,我们选择把所有流量都*2,最后再/2。
$ ans=sum(全部收益)- 最小割 $
p.s.用邻接表建图的时候先把每个点选单科的边连上,再练同时选的收益,否则会重
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=105,E=1000005,inf=1e9,P=500005;
int n,m,a[N][N],b[N][N],c[N][N],d[N][N],s,t,sum,cnt=1,h[P],le[N*N];
struct qwe
{
int ne,to,va;
}e[E];
int read()
{
int r=0;
char p=getchar();
while(p<'0'||p>'9')
p=getchar();
while(p>='0'&&p<='9')
{
r=r*10+p-48;
p=getchar();
}
return r;
}
void add(int u,int v,int w)
{
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
e[cnt].va=w;
h[u]=cnt;
}
bool bfs()
{
queue<int>q;
memset(le,0,sizeof(le));
le[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();//cout<<u<<"AAAAAAAAAAAA"<<endl;
q.pop();
for(int i=h[u];i;i=e[i].ne)
if(e[i].va&&!le[e[i].to])
{
le[e[i].to]=le[u]+1;
q.push(e[i].to);
}
}
// for(int i=0;i<=5;i++)
// cout<<le[i]<<" ";
return le[t];
}
int dfs(int u,int f)
{//cout<<u<<" "<<f<<endl;
if(u==t)
{
//cout<<"!!";
return f;
}
int used=0;
for(int i=h[u];i;i=e[i].ne)
{
//cout<<u<<" "<<e[i].to<<" "<<e[i].va<<endl;;
if(e[i].va>0&&le[e[i].to]==le[u]+1)
{//cout<<"OK"<<endl;
int w=dfs(e[i].to,min(f-used,e[i].va));
e[i].va-=w;
e[i^1].va+=w;
used+=w;
if(used==f)
return f;
}
}
if(!used)
le[u]=-1;
return used;
}
int dinic()
{
int ans=0;
while(bfs())
ans+=dfs(s,inf);//,cout<<ans<<endl;
return ans;
}
int main()
{
n=read(),m=read();
s=0,t=n*m+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
a[i][j]=read(),sum+=a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
b[i][j]=read(),sum+=b[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
int x=(i-1)*m+j;
add(s,x,b[i][j]<<1);
add(x,s,0);
add(x,t,a[i][j]<<1);
add(t,x,0);
}
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
c[i][j]=read(),sum+=c[i][j];
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
d[i][j]=read(),sum+=d[i][j];
for(int i=1;i<n;i++)
for(int j=1;j<=m;j++)
{
int x=(i-1)*m+j,y=i*m+j;
add(s,x,d[i][j]);
add(x,s,0);
add(s,y,d[i][j]);
add(y,s,0);
add(x,y,c[i][j]+d[i][j]);
add(y,x,c[i][j]+d[i][j]);
add(x,t,c[i][j]);
add(t,x,0);
add(y,t,c[i][j]);
add(t,y,0);
}
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
c[i][j]=read(),sum+=c[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
d[i][j]=read(),sum+=d[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<m;j++)
{
int x=(i-1)*m+j,y=(i-1)*m+j+1;
add(s,x,d[i][j]);
add(x,s,0);
add(s,y,d[i][j]);
add(y,s,0);
add(x,y,c[i][j]+d[i][j]);
add(y,x,c[i][j]+d[i][j]);
add(x,t,c[i][j]);
add(t,x,0);
add(y,t,c[i][j]);
add(t,y,0);
}
printf("%d\n",sum-(dinic()>>1));
return 0;
}



