bzoj 1814: Ural 1519 Formula 1【插头dp】
设f[i][j][s]为轮廓线推到格子(i,j),状态为s的方案数
括号表示一段线的左端和右端,表示成左括号和右括号,状压的时候用1和2表示,0表示已经闭合
下面的蓝线是黄色格子的轮廓线,dp转移要把它转到橙色轮廓线,设已经在状压的s中取到两条边的状态记为b1,b2
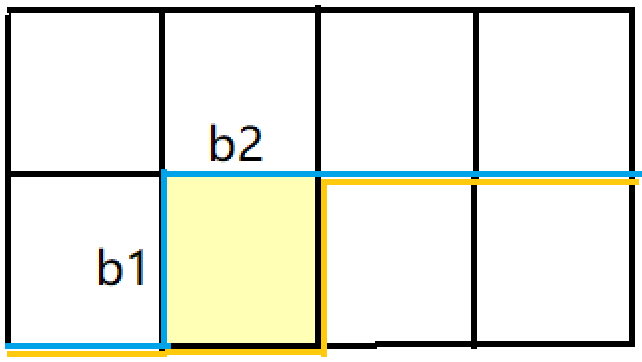
然后分很多情况讨论:
(i,j)是障碍:那就只能什么都不放的转移,也就是只能从b1=0,b2=0转移到新轮廓线的b1=0,b2=0
if(!a[i][j])
{
if(!b1&&!b2)
add(x,v);
}
b1=0,b2=0:因为不能空,所以只能转移一个拐角
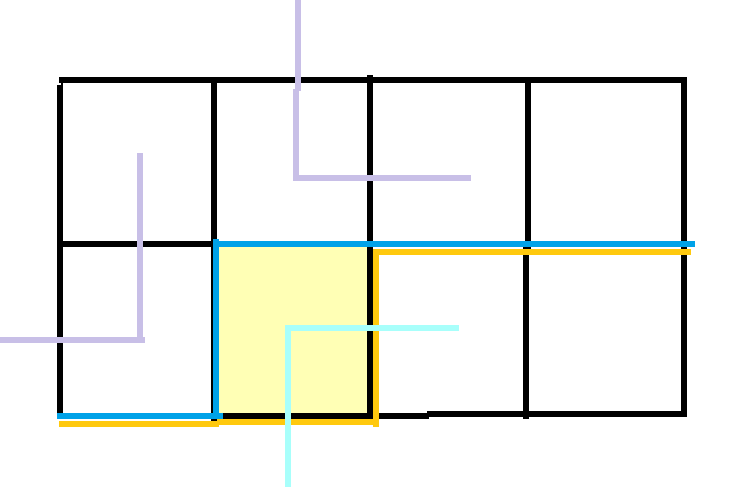
else if(!b1&&!b2)
{
if(a[i+1][j]&&a[i][j+1])
add(x+b[j-1]+2*b[j],v);
}
b1=0或者b2=0:根据有无障碍判断能不能转移,如果(i,j+1),(i+1,j)都没有障碍的话就有两种转移,以b1=0,b2!=0为例:
一种是接上然后拐弯,这样转移后的轮廓线括号状态不变
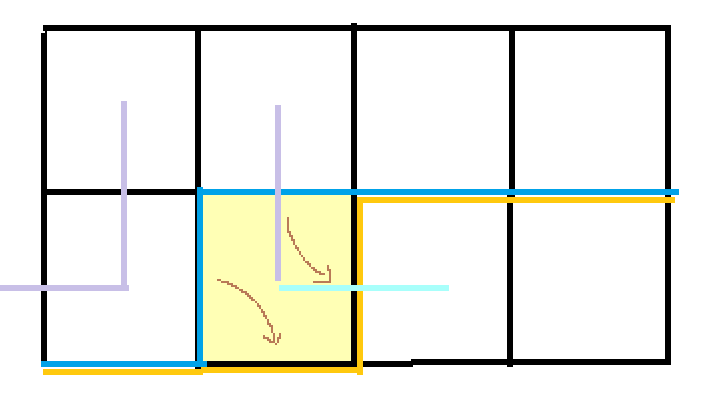
另一种是接上直着走,转移后的轮廓线括号状态b1b2互换
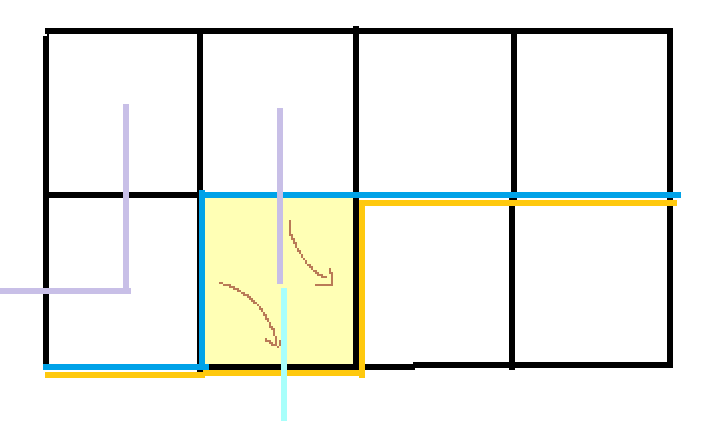
b1!=0,b2=0同理
else if(!b1&&b2)
{
if(a[i][j+1])
add(x,v);
if(a[i+1][j])
add(x-b[j]*b2+b[j-1]*b2,v);
}
else if(b1&&!b2)
{
if(a[i][j+1])
add(x-b[j-1]*b1+b[j]*b1,v);
if(a[i+1][j])
add(x,v);
}
b1=b2=1或2:这样这两条线会在(i,j)格子连起来,两队括号合成一对,以b1=b2=1为例:
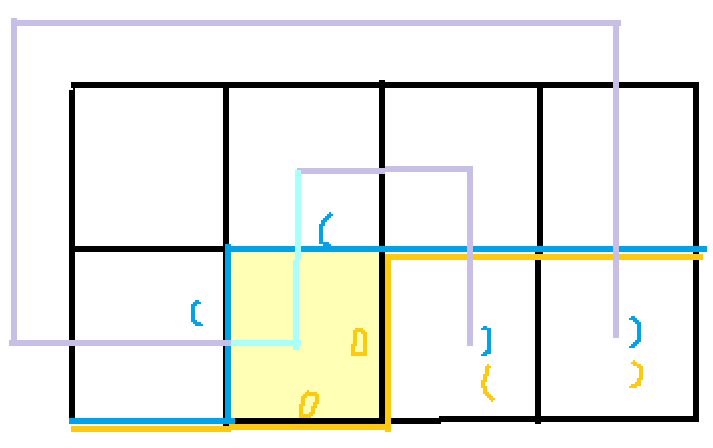
else if(b1==1&&b2==1)
{
for(int t=1,l=j+1;l<=m;l++)
{
if((x>>(l*2))%4==1)
t++;
if((x>>(l*2))%4==2)
t--;
if(!t)
{
add(x-b[j]-b[j-1]-b[l],v);
break;
}
}
}
else if(b1==2&&b2==2)
{
for(int t=1,l=j-2;l>=0;l--)
{
if((x>>(l*2))%4==1)
t--;
if((x>>(l*2))%4==2)
t++;
if(!t)
{
add(x+b[l]-2*b[j]-2*b[j-1],v);
break;
}
}
}
b1=2,b2=1:和上面差不多,就是把这两个括号合并就行了
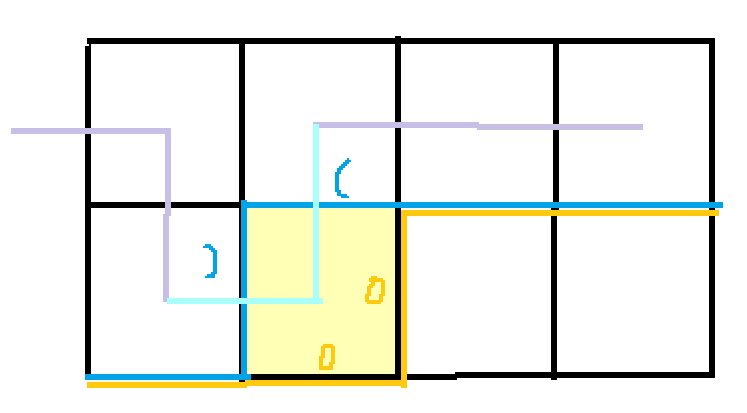
else if(b1==2&&b2==1)
add(x-2*b[j-1]-b[j],v);
b1=1,b2=2:这个只有到最后一个没障碍的点才能转移,因为这是把一条线连成一个回路的最后一步
其实不用转移,直接加进答案就行了
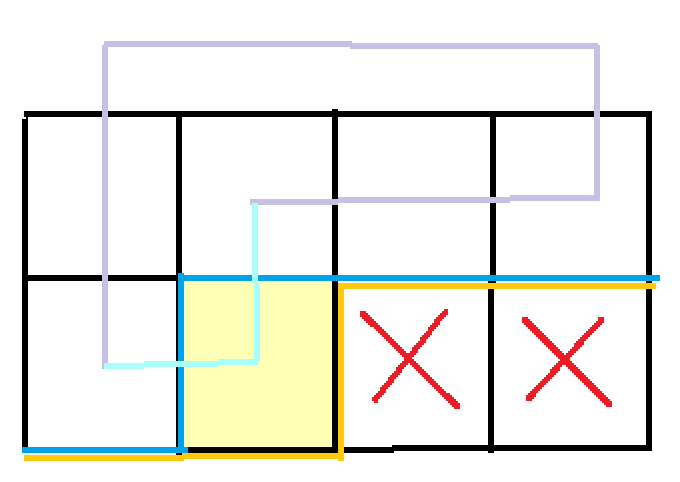
else if(i==tx&&j==ty)
ans+=v;
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=15,mod=299989;
int n,m,la,nw,a[N][N],b[N],c[2],h[300005],tx,ty;
long long ans;
char s[N];
struct qwe
{
int ne,to[2];
long long va[2];
}e[300005];
void add(int x,long long v)
{
int u=x%mod+1;
for(int i=h[u];i;i=e[i].ne)
if(e[i].to[nw]==x)
{
e[i].va[nw]+=v;
return;
}
e[++c[nw]].ne=h[u];
e[c[nw]].to[nw]=x;
e[c[nw]].va[nw]=v;
h[u]=c[nw];
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
for(int j=1;j<=m;j++)
if(s[j]=='.')
a[i][j]=1,tx=i,ty=j;
}
b[0]=1;
for(int i=1;i<=12;i++)
b[i]=b[i-1]<<2;
c[0]=1,e[1].va[0]=1,e[1].to[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c[nw];j++)
e[j].to[nw]<<=2;
for(int j=1;j<=m;j++)
{
la=nw,nw^=1;
memset(h,0,sizeof(h));
c[nw]=0;
for(int k=1;k<=c[la];k++)
{
int x=e[k].to[la],b1=(x>>(j*2-2))%4,b2=(x>>(j*2))%4;
long long v=e[k].va[la];
if(!a[i][j])
{
if(!b1&&!b2)
add(x,v);
}
else if(!b1&&!b2)
{
if(a[i+1][j]&&a[i][j+1])
add(x+b[j-1]+2*b[j],v);
}
else if(!b1&&b2)
{
if(a[i][j+1])
add(x,v);
if(a[i+1][j])
add(x-b[j]*b2+b[j-1]*b2,v);
}
else if(b1&&!b2)
{
if(a[i][j+1])
add(x-b[j-1]*b1+b[j]*b1,v);
if(a[i+1][j])
add(x,v);
}
else if(b1==1&&b2==1)
{
for(int t=1,l=j+1;l<=m;l++)
{
if((x>>(l*2))%4==1)
t++;
if((x>>(l*2))%4==2)
t--;
if(!t)
{
add(x-b[j]-b[j-1]-b[l],v);
break;
}
}
}
else if(b1==2&&b2==2)
{
for(int t=1,l=j-2;l>=0;l--)
{
if((x>>(l*2))%4==1)
t--;
if((x>>(l*2))%4==2)
t++;
if(!t)
{
add(x+b[l]-2*b[j]-2*b[j-1],v);
break;
}
}
}
else if(b1==2&&b2==1)
add(x-2*b[j-1]-b[j],v);
else if(i==tx&&j==ty)
ans+=v;
}
}
}
printf("%lld\n",ans);
return 0;
}



