NOI2007 项链工厂
题目背景
T公司是一家专门生产彩色珠子项链的公司,其生产的项链设计新颖、款式多样、价格适中,广受青年人的喜爱。
最近T公司打算推出一款项链自助生产系统,使用该系统顾客可以自行设计心目中的美丽项链。该项链自助生产系
统包括硬件系统与软件系统,软件系统与用户进行交互并控制硬件系统,硬件系统接受软件系统的命令生产指定的
项链。该系统的硬件系统已经完成,而软件系统尚未开发,T公司的人找到了正在参加全国信息学竞赛的你,你能
帮助T公司编写一个软件模拟系统吗?
题目描述
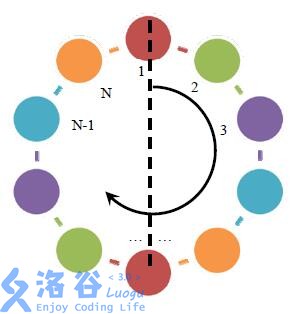
一条项链包含 N 个珠子,每个珠子的颜色是 1,2,…,c 中的一种。项链
被固定在一个平板上,平板的某个位置被标记位置 1 ,按顺时针方向其他位置被记为 2,3,…,N。
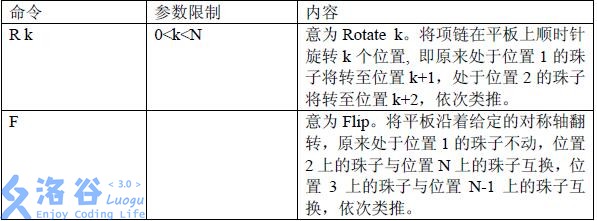
你将要编写的软件系统应支持如下命令:
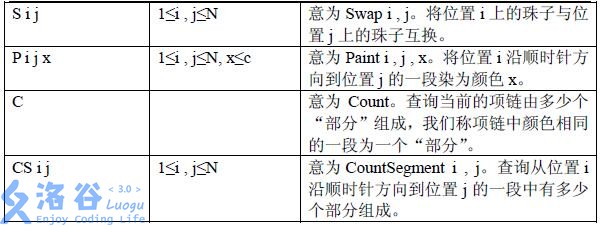
输入格式
输入文件第一行包含两个整数N, c,分别表示项链包含的珠子数目以及颜色数目。
第二行包含N 个整数,x1, x2…, xn,表示从位置1 到位置N 的珠子的颜色,1 ≤ xi ≤ c。
第三行包含一个整数Q,表示命令数目。
接下来的Q 行每行一条命令,如上文所述。
输出格式
对于每一个C 和CS 命令,应输出一个整数代表相应的答案。
输入输出样例
5 3 1 2 3 2 1 4 C R 2 P 5 5 2 CS 4 1
4 1
说明/提示
【数据规模和约定】
对于60%的数据,N ≤ 1 000,Q ≤ 1 000;
对于100%的数据,N ≤ 500 000,Q ≤ 500 000,c ≤ 1 000。
关于旋转和翻转
注意旋转命令旋转“珠子”但不改变“位置”的编号,而反转命令始终以位置 1 为对称轴。例如当 N=10 时,项链上的位置编号如图1:
但注意此时项链上的位置编号仍然如图1所示,于是翻转的对称轴不变。因而再执行一次“F”命令时,项链的颜色如图4所示。


关于CountSegment命令
CS命令表示查询一个“线段”中有多少个“部分”。尤其注意当查询的长度等于 N 时,我们仍然将查询部分作为“线段”理解。
例如在图4所示的情况中,执行“CS 1 10”命令,查询从位置 1 开始到位置 10 结束的这个长度为 10 的线段中有多少个“部分”,于是得到返回值 3 。与之形成对照的是,若执行“C”命令,返回值则为 2
思路:我直接服了这个题了,细节是真的很多。不过整体思路还是挺简单的,我们一步步来看,如果忽略掉rotate和flip操作,这题就是个线段树裸题,那么现在怎么办呢?考虑两个方向:1.更换新的数据结构,来处理rotate和flip,但是需要维护的数据太多,虽然也能做,但是未免过于麻烦;2.试试通过某种方法把这两个操作处理掉。我这里用的是方法2,我们维护两个变量ks和rev,表示旋转的幅度和是否翻转,通过简单的找规律和模拟,可以得出,当询问一个位置pos时,当前pos位置珠子的编号为:1.当rev==0即珠子未翻转时,编号=pos-ks;2.当rev==1即珠子翻转时,编号=ks-pos+2。不要忘记取模。于是,我们每次rotate的时候就将对应的ks加k,每次flip的时候将ks=n-ks(想想为什么),并且将rev取反。这样就能直接通过数学演算忽视掉rotate和flip的影响。
(一个细节,当询问所有珠子的时候(即C命令),如果所有珠子颜色均相同,则答案为1而非0)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 const int N = 5e5 + 5; 8 inline int read() 9 { 10 int ret = 0; 11 char c = getchar(); 12 while(c < '0' || c > '9') c = getchar(); 13 while(c >= '0' && c <= '9') 14 {ret = ret * 10 + c - '0'; c = getchar();} 15 return ret; 16 } 17 int ks = 0, rev = 0; 18 int n, cl, m; 19 int num[N]; 20 #define ls p << 1 21 #define rs p << 1 | 1 22 struct seg{ 23 int l, r; 24 int add, lc, rc, s; 25 }tr[N << 2]; 26 inline void update(int p) 27 { 28 tr[p].lc = tr[ls].lc; 29 tr[p].rc = tr[rs].rc; 30 tr[p].s = tr[ls].s + tr[rs].s - (tr[ls].rc == tr[rs].lc ? 1 : 0); 31 } 32 void build(int p, int l, int r) 33 { 34 tr[p].l = l; 35 tr[p].r = r; 36 if(l == r) 37 { 38 tr[p].lc = tr[p].rc = num[l]; 39 tr[p].s = 1; 40 return; 41 } 42 int mid = l + r >> 1; 43 build(ls, l, mid); 44 build(rs, mid + 1, r); 45 update(p); 46 } 47 inline void pushdown(int p) 48 { 49 if(tr[p].add) 50 { 51 int v = tr[p].add; 52 tr[p].add = 0; 53 tr[ls].add = v; 54 tr[ls].lc = tr[ls].rc = v; 55 tr[ls].s = 1; 56 tr[rs].add = v; 57 tr[rs].lc = tr[rs].rc = v; 58 tr[rs].s = 1; 59 } 60 } 61 void modify(int p, int l, int r, int v) 62 { 63 if(l <= tr[p].l && r >= tr[p].r) 64 { 65 tr[p].add = v; 66 tr[p].lc = tr[p].rc = v; 67 tr[p].s = 1; 68 return; 69 } 70 pushdown(p); 71 int mid = tr[p].l + tr[p].r >> 1; 72 if(l <= mid) modify(ls, l, r, v); 73 if(r > mid) modify(rs, l, r, v); 74 update(p); 75 } 76 int ask_color(int p, int pos) 77 { 78 if(tr[p].l == tr[p].r) return tr[p].lc; 79 int mid = tr[p].l + tr[p].r >> 1; 80 pushdown(p); 81 if(pos <= mid) return ask_color(ls, pos); 82 else return ask_color(rs, pos); 83 } 84 inline int mo(int x) 85 { 86 x = (x % n + n) % n; 87 if(!x) x = n; 88 return x; 89 } 90 inline int val(int x) 91 { 92 if(!rev) return mo(x - ks); 93 return mo(ks - x + 2); 94 } 95 seg query(int p, int l, int r) 96 { 97 if(l <= tr[p].l && r >= tr[p].r) return tr[p]; 98 int mid = tr[p].l + tr[p].r >> 1; 99 seg lz = {0, 0, 0, 0, 0, 0}; 100 seg rz = {0, 0, 0, 0, 0, 0}; 101 seg ret; 102 pushdown(p); 103 if(l <= mid) lz = query(ls, l, r); 104 if(r > mid) rz = query(rs, l, r); 105 if(!lz.s) ret = {0, 0, 0, rz.lc, rz.rc, rz.s}; 106 else if(!rz.s) ret = {0, 0, 0, lz.lc, lz.rc, lz.s}; 107 else ret = {0, 0, 0, lz.lc, rz.rc, lz.s + rz.s - (lz.rc == rz.lc ? 1 : 0)}; 108 return ret; 109 } 110 int main() 111 { 112 n = read(), cl = read(); 113 for(int i = 1; i <= n; i ++) num[i] = read(); 114 build(1, 1, n); 115 m = read(); 116 char op[5]; 117 int a, b, c, d, A, B; 118 seg C, D; 119 for(int i = 1; i <= m; i ++) 120 { 121 scanf("%s", op); 122 if(op[0] == 'R') a = read(), ks += a, ks %= n; 123 else if(op[0] == 'F') ks = n - ks, ks %= n, rev ^= 1; 124 else if(op[0] == 'S') 125 { 126 a = read(), b = read(); 127 a = val(a), b = val(b); 128 c = ask_color(1, a), d = ask_color(1, b); 129 modify(1, a, a, d), modify(1, b, b, c); 130 } 131 else if(op[0] == 'P') 132 { 133 a = read(), b = read(), c = read(); 134 a = val(a), b = val(b); 135 A = min(a, b), B = max(a, b); 136 if((((a < b) ^ rev) == 1) || (a == b)) modify(1, A, B, c); 137 else modify(1, 1, A, c), modify(1, B, n, c); 138 } 139 else if(op[0] == 'C') 140 { 141 if(op[1] == 'S') 142 { 143 a = read(), b = read(); 144 a = val(a), b = val(b); 145 A = min(a, b), B = max(a, b); 146 if((((a < b) ^ rev) == 1) || (a == b)) printf("%d\n", query(1, A, B).s); 147 else 148 { 149 C = query(1, 1, A), D = query(1, B, n); 150 printf("%d\n", C.s + D.s - (C.lc == D.rc ? 1 : 0)); 151 } 152 } 153 else 154 { 155 C = query(1, 1, n); 156 printf("%d\n", max(1, C.s - (C.lc == C.rc ? 1 : 0))); 157 } 158 } 159 } 160 return 0; 161 }



