洛谷 P4001 [ICPC-Beijing 2006]狼抓兔子
题目描述
现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到,但抓兔子还是比较在行的,而且现在的兔子还比较笨,它们只有两个窝,现在你做为狼王,面对下面这样一个网格的地形:
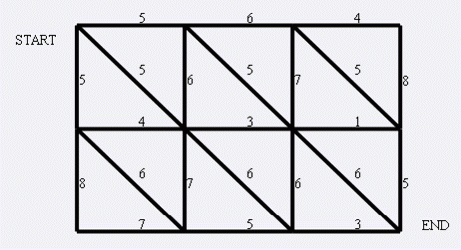
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数,道路是无向的. 左上角和右下角为兔子的两个窝,开始时所有的兔子都聚集在左上角(1,1)的窝里,现在它们要跑到右下角(N,M)的窝中去,狼王开始伏击这些兔子.当然为了保险起见,如果一条道路上最多通过的兔子数为K,狼王需要安排同样数量的K只狼,才能完全封锁这条道路,你需要帮助狼王安排一个伏击方案,使得在将兔子一网打尽的前提下,参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。
输入格式
第一行为N,M.表示网格的大小,N,M均小于等于1000.
接下来分三部分
第一部分共N行,每行M-1个数,表示横向道路的权值.
第二部分共N-1行,每行M个数,表示纵向道路的权值.
第三部分共N-1行,每行M-1个数,表示斜向道路的权值.
输出格式
输出一个整数,表示参与伏击的狼的最小数量.
输入输出样例
输入 #1
3 4 5 6 4 4 3 1 7 5 3 5 6 7 8 8 7 6 5 5 5 5 6 6 6
输出 #1
14
思路:这个题是一道很显然的最小割,可以用最小割最大流定理去证明,最小割=最大流,然后用dinic解决该问题。然而我们看看数据范围,n,m<=1000,也就是说节点数量高达10^6,
很显然朴素的dinic是过不了的,然而因为本题数据过于水,所以对dinic在加一些玄学优化也是能过得去的。然而,我这里要说一个对这类问题的一个最为有效的方法:平面图转对偶图。
对偶图的解释请参考相关书籍,这里不详细介绍。从题目中我们可以发现题目中给的图具有特殊性质,即每个方格都可以分成两个三角形,且这些方格与这些方格分成的三角形呈网格状排列,
这其实对于一个平面图来说,转换为其对应的对偶图是相对容易的,我们可以将原图中的起点S与终点T之间连一条线,这条线包围的面就作为对偶图的终点,而起点就是其全集的补。
建图比较复杂,写在main函数里面了。另外还要对n==1或m==1的情况进行特判。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 using namespace std; 7 const int N = 2e6 + 10; 8 const int M = 6e6 + 10; 9 int read() 10 { 11 int ret = 0; 12 char ch = getchar(); 13 while(ch < '0' || ch > '9') ch = getchar(); 14 while(ch >= '0' && ch <= '9') 15 {ret = ret * 10 + ch - '0'; ch = getchar();} 16 return ret; 17 } 18 struct edge{ 19 int to, nxt, dis; 20 }e[M << 1]; 21 int head[N], tot = 0; 22 void adde(int f, int t, int d) 23 { 24 e[++ tot] = (edge){t, head[f], d}; 25 head[f] = tot; 26 } 27 int n, m, st, ed; 28 int dist[N], vis[N]; 29 struct node{ 30 int id, dis; 31 bool operator < (const node A) const{ 32 return A.dis < dis; 33 } 34 }; 35 priority_queue <node> q; 36 void dij() 37 { 38 memset(dist, 0x3f, sizeof dist); 39 memset(vis, 0, sizeof vis); 40 q.push((node){st, 0}); 41 dist[st] = 0; 42 while(!q.empty()) 43 { 44 int u = q.top().id; 45 q.pop(); 46 if(vis[u]) continue; 47 vis[u] = 1; 48 for(int i = head[u]; i; i = e[i].nxt) 49 { 50 int v = e[i].to; 51 if(dist[v] > dist[u] + e[i].dis) 52 { 53 dist[v] = dist[u] + e[i].dis; 54 q.push((node){v, dist[v]}); 55 } 56 } 57 } 58 } 59 int val(int r, int c, int tmp) 60 { 61 return (r - 1) * (m - 1) + c + tmp * (m - 1) * (n - 1); 62 } 63 int main() 64 { 65 scanf("%d%d", &n, &m); 66 //if(n == 1 || m == 1) {printf("1\n"); return 0;} 67 int x; 68 int minn = 0x3f3f3f3f; 69 st = 0, ed = 2 * m * n + 1; 70 for(int i = 1; i <= n; i ++) 71 for(int j = 1; j <= m - 1; j ++) 72 { 73 scanf("%d", &x); 74 minn = min(minn, x); 75 if(i == 1) 76 { 77 adde(val(i, j, 0), st, x); 78 adde(st, val(i, j, 0), x); 79 } 80 else if(i == n) 81 { 82 adde(ed, val(i - 1, j, 1), x); 83 adde(val(i - 1, j, 1), ed, x); 84 } 85 else 86 { 87 adde(val(i, j, 0), val(i - 1, j, 1), x); 88 adde(val(i - 1, j, 1), val(i, j, 0), x); 89 } 90 } 91 for(int i = 1; i <= n - 1; i ++) 92 for(int j = 1; j <= m; j ++) 93 { 94 scanf("%d", &x); 95 minn = min(minn, x); 96 if(j == 1) 97 { 98 adde(ed, val(i, j, 1), x); 99 adde(val(i, j, 1), ed, x); 100 } 101 else if(j == m) 102 { 103 adde(val(i, j - 1, 0), st, x); 104 adde(st, val(i, j - 1, 0), x); 105 } 106 else 107 { 108 adde(val(i, j, 1), val(i, j - 1, 0), x); 109 adde(val(i, j - 1, 0), val(i, j, 1), x); 110 } 111 } 112 for(int i = 1; i <= n - 1; i ++) 113 for(int j = 1; j <= m - 1; j ++) 114 { 115 scanf("%d", &x); 116 adde(val(i, j, 0), val(i, j, 1), x); 117 adde(val(i, j, 1), val(i, j, 0), x); 118 } 119 dij(); 120 if(n == 1 || m == 1) printf("%d\n", minn); 121 else printf("%d\n", dist[ed]); 122 return 0; 123 }



