浅谈树状数组
还是区间求和区间修改的问题,我们使用线段树解决以后发现编程复杂度比较大
在这里介绍一个简单的数据结构,树状数组。
树状数组的优势是编程复杂度小,常数小,时间复杂度也不错
树状数组的查询,修改,都是LOG(N)级别的
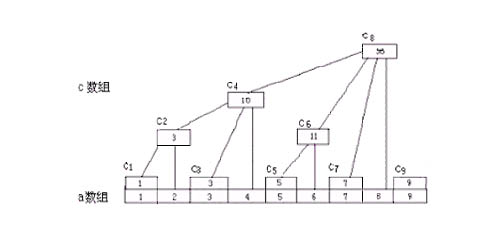
下面来分析一下上面那个图看能得出什么规律:
据图可知:c1=a1,c2=a1+a2,c3=a3,c4=a1+a2+a3+a4,c5=a5,c6=a5+a6,c7=a7,c8=a1+a2+a3+a4+a5+a6+a7+a8,c9=a9,c10=a9+a10,c11=a11........c16=a1+a2+a3+a4+a5+.......+a16。
分析上面的几组式子可知,当 i 为奇数时,ci=ai ;当 i 为偶数时,就要看 i 的因子中最多有二的多少次幂,例如,6 的因子中有 2 的一次幂,等于 2 ,所以 c6=a5+a6(由六向前数两个数的和),4 的因子中有 2 的两次幂,等于 4 ,所以 c4=a1+a2+a3+a4(由四向前数四个数的和)。
(一)有公式:cn=a(n-a^k+1)+.........+an(其中 k 为 n 的二进制表示中从右往左数的 0 的个数)。
那么,如何求 a^k 呢?求法如下:

function lowbit(x:longint):longint;
begin
exit(x and (-x))
end;
lowbit的返回值就是2^k
答案很简单:2^k=i&(i^(i-1)) ,也就是i&(-i)
下面进行解释:
以i=6为例(注意:a_x表示数字a是x进制表示形式):
(i)_10 = (0110)_2
(i-1)_10=(0101)_2
i xor (i-1) =(0011)_2
i and (i xor (i-1)) =(0010)_2
2^k = 2
C[6] = C[6-2+1]+…+A[6]=A[5]+A[6]
而我们求和与修改的时候就特别好办了

function lowbit(x:longint):longint;
begin
exit(x and (-x));
end;
function getsum(pos:longint):longint;
var ans:longint;
begin
ans:=0;
while pos>0 do
begin
inc(sum,tree[pos]);
dec(pos,lowbit(pos));
end;
exit(ans);
end;
procedure modify(pos,delta:longint);
begin
while pos<=n do
begin
inc(tree[pos],delta);
inc(pos,lowbit(x));
end;
end;
记住,查询区间[l,r]的和时候应该ans:=getsum(r)-getsum(l-1);
求数列的前n项和,只需找到n以前的所有最大子树,把其根节点的C加起来即可。不难发现,这些树的数目是n在二进制时1的个数,或者说是把n展开成2的幂方和时的项数。
代码如下:

const maxn=100010;
var val,tree:array [0..maxn] of longint;
n:longint;
function lowbit(x:longint):longint;
begin
exit(x and (-x));
end;
function getsum(pos:longint):longint;
var ans:longint;
begin
ans:=0;
while pos>0 do
begin
inc(ans,tree[pos]);
dec(pos,lowbit(pos));
end;
exit(ans);
end;
procedure modify(pos,delta:longint);
begin
while pos<=n do
begin
inc(tree[pos],delta);
inc(pos,lowbit(pos));
end;
end;
procedure main;
var i,m,l,r:longint;
begin
read(n);
for i:=1 to n do
begin
read(val[i]);
modify(i,val[i]);
end;
read(m);
for i:=1 to m do
begin
read(l,r);
writeln(getsum(r)-getsum(l-1));
end;
end;
begin
main;
end.




