[Luogu 1312] noip11 Mayan游戏
[Luogu 1312] noip11 Mayan游戏
Problem:
Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个 7 行5 列的棋盘,上面堆放着一些方块,方块不能悬空堆放,即方块必须放在最下面一行,或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块,消除方块的规则如下:
1 、每步移动可以且仅可以沿横向(即向左或向右)拖动某一方块一格:当拖动这一方块时,如果拖动后到达的位置(以下称目标位置)也有方块,那么这两个方块将交换位置(参见输入输出样例说明中的图6 到图7 );如果目标位置上没有方块,那么被拖动的方块将从原来的竖列中抽出,并从目标位置上掉落(直到不悬空,参见下面图1 和图2);
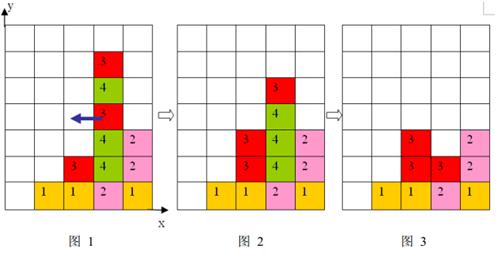
2 、任一时刻,如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块,则它们将立即被消除(参见图1 到图3)。
注意:
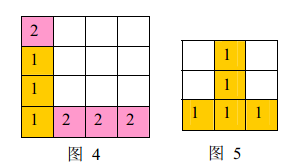
a) 如果同时有多组方块满足消除条件,几组方块会同时被消除(例如下面图4 ,三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除,最后剩下一个颜色为 2 的方块)。
b) 当出现行和列都满足消除条件且行列共享某个方块时,行和列上满足消除条件的所有方块会被同时消除(例如下面图5 所示的情形,5 个方块会同时被消除)。
3 、方块消除之后,消除位置之上的方块将掉落,掉落后可能会引起新的方块消除。注意:掉落的过程中将不会有方块的消除。
上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为(0, 0 ),将位于(3, 3 )的方块向左移动之后,游戏界面从图 1 变成图 2 所示的状态,此时在一竖列上有连续三块颜色为4 的方块,满足消除条件,消除连续3 块颜色为4 的方块后,上方的颜色为3 的方块掉落,形成图 3 所示的局面。
输入输出格式
输入格式:
第一行为一个正整数n ,表示要求游戏通关的步数。
接下来的5 行,描述 7*5 的游戏界面。每行若干个整数,每两个整数之间用一个空格隔开,每行以一个0 结束,自下向上表示每竖列方块的颜色编号(颜色不多于10种,从1 开始顺序编号,相同数字表示相同颜色)。
输入数据保证初始棋盘中没有可以消除的方块。
输出格式:
如果有解决方案,输出 n 行,每行包含 3 个整数x,y,g ,表示一次移动,每两个整数之间用一个空格隔开,其中(x ,y)表示要移动的方块的坐标,g 表示移动的方向,1 表示向右移动,-1表示向左移动。注意:多组解时,按照 x 为第一关健字,y 为第二关健字,1优先于-1 ,给出一组字典序最小的解。游戏界面左下角的坐标为(0 ,0 )。
如果没有解决方案,输出一行,包含一个整数-1。
输入输出样例
说明
【输入输出样例说明】
按箭头方向的顺序分别为图6 到图11
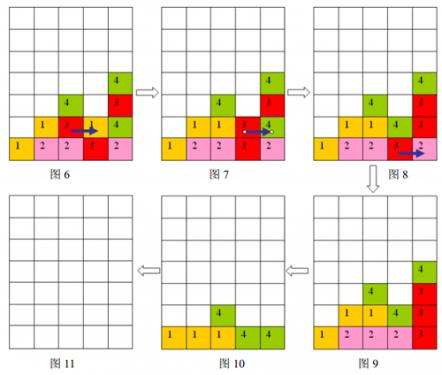
样例输入的游戏局面如上面第一个图片所示,依次移动的三步是:(2 ,1 )处的方格向右移动,(3,1 )处的方格向右移动,(3 ,0)处的方格向右移动,最后可以将棋盘上所有方块消除。
【数据范围】
对于30% 的数据,初始棋盘上的方块都在棋盘的最下面一行;
对于100%的数据,0 < n ≤ 5 。
Solution:
对于这种操作复杂的题目,先整理一下题意:
(1)给你一个7*5的矩阵,里面包含1-10的数字,每个数字代表一个方块
(2)你可以将其中一个方块往左或往右移一格,假设这格是(i,j),如果(i+1,j)这格有方块,则交换两个位置,否则将其平移一格
(3)在操作之后,方块会自然落下,即没有方块凌空
(4)以上三步结束后进行消除,若有连续三个或者三个以上相同颜色的方块,则会消除,具体消除细节参看题目红字
(5)求一组字典序最小的解,使得所有的方块都能消除
读完了长长的题目,你已完成了1/3的工程,下面我们思考如何去做
如果简要的说,这道题其实只有三个操作:移动,掉落,消块
另外由于题目规定的步数不超过5步,所以比较容易想到搜索。那么你已经完成了2/3的题目
最后可能就是程序的一些细节,和部分剪枝,先上代码,再解释

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<algorithm> 6 #include<vector> 7 using namespace std; 8 int a[10][10],lim,x[10],y[10],w[10],xx,tot=0; 9 10 void add(int i,int j,int ww){x[++tot]=i; y[tot]=j; w[tot]=ww;} 11 void del(){x[tot]=y[tot]=w[tot]=0; tot--; } 12 void print(){ 13 bool flag=1; 14 for (int i=1;i<=5;++i) 15 if (a[i][1]){flag=0; break;} 16 if (flag){ 17 for (int i=1;i<=lim;++i) printf("%d %d %d\n",x[i]-1,y[i]-1,w[i]); 18 exit(0); 19 } return; 20 } 21 //about ans 22 vector<int>num; 23 void drop(int x){ 24 for (int i=1;i<=7;++i) 25 if (a[x][i]>0) num.push_back(a[x][i]),a[x][i]=0; 26 for (int i=0;i<num.size();++i) 27 a[x][i+1]=num[i]; 28 num.clear(); 29 } 30 31 void clear(){ 32 bool flag=1; 33 while (flag){ 34 flag=0; int res[10][10]; 35 memcpy(res,a,sizeof(res)); 36 for (int i=1;i<=5;++i) 37 for (int j=1;j<=7;++j) if (res[i][j]){ 38 if (i>1&&i<5 && res[i-1][j]==res[i][j]&&res[i][j]==res[i+1][j]){ 39 a[i-1][j]=a[i][j]=a[i+1][j]=0; 40 flag=1; 41 } 42 if (j>1&&j<7 && res[i][j-1]==res[i][j]&&res[i][j]==res[i][j+1]){ 43 a[i][j-1]=a[i][j]=a[i][j+1]=0; 44 flag=1; 45 } 46 } 47 if (!flag) return; 48 for (int i=1;i<=5;++i) drop(i); 49 } 50 } 51 52 void dfs(int dep){ 53 if (dep==lim+1){ 54 print(); return; 55 } 56 int res[10][10]; 57 memcpy(res,a,sizeof(res)); 58 for (int i=1;i<=5;++i) 59 for (int j=1;j<=7;++j) if (a[i][j]){ 60 if (i!=5 && a[i][j]!=a[i+1][j]){ 61 62 swap(a[i][j],a[i+1][j]); 63 drop(i); drop(i+1); 64 clear(); add(i,j,1); 65 dfs(dep+1); del(); 66 memcpy(a,res,sizeof(a)); 67 68 }//right 69 if (i!=1 && a[i-1][j]==0){ 70 71 swap(a[i][j],a[i-1][j]); 72 drop(i); drop(i-1); 73 clear(); add(i,j,-1); 74 dfs(dep+1); del(); 75 memcpy(a,res,sizeof(a)); 76 77 }//left 78 } else break; 79 } 80 81 int main(){ 82 scanf("%d",&lim); 83 for (int i=1;i<=5;++i){ 84 int cnt=0; 85 while (scanf("%d",&xx)&&xx!=0) a[i][++cnt]=xx; 86 } 87 dfs(1); puts("-1"); 88 return 0; 89 }
剪枝:
(1)在中间的时候向右交换(左边那个向右边移动字典序更小)
(2)当左边没有格的时候向左移动
(3)当右边的格子和自己相同时跳过
注意:
(1)dfs的时候如果你要备份当前状态,数组要在过程中定义,不能定义为全局变量
(2)消块时,你同样要备份当前的状态,否则就无法消去类似十字架的方块
(3)从现在开始注意细节,祝各位读者和自己noip加油



 浙公网安备 33010602011771号
浙公网安备 33010602011771号