[Luogu 1850] noip16 换教室

[Luogu 1850] noip16 换教室

好久没有更博客了，先唠嗑一会，花了两天的空闲时间大致做完了昨年的noip真题

虽然在经过思考大部分题目都可出解（天天爱跑步除外），但是并不知道考试时候造化如何。

总之自己这段时间多做好事，多积攒RP，每天RP++

Description

Solution：

首先当你看完这个到题的时候，你应该想到先用floyd跑出任意两点的最短路，这个不解释

然后又是这种求期望值最小，很明显也会想到DP的做法

那么DP的方程？通过发现对于当前第i个课程教室的期望是跟前一个课程的选择与否有关的，

那么最后我们的状态可以表示为 f[n][m][0..1]

接下去就比较容易了，只是需要耐心仔细的分类讨论

1、当前的课不换的情况：

（1）上一节课也没换；

（2）上一节课换了----成功 or 不成功；

2、当前的课换的情况：

（1）当前课成功换了：

a、上一节课换了----上一节课成功 or 不成功

b、上一节课没换；

（2）当前的课换了失败：

a、上一节课换了----上一节课成功 or 不成功

b、上一节课没换；

最后总结一下就是

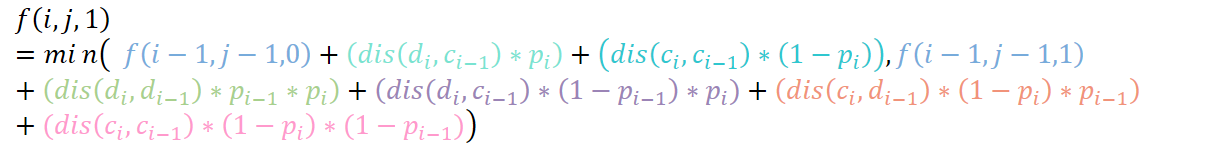
那么就完成了

注意：转移时候因为多次出现距离可预先用cc，cd，dc，dd来表示 c[i-1] 到 c[i] 等等的距离

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=500,M=2010;
int c[M],d[M],dis[N][N],x,y,z,n,m,v,e;
double f[M][M][2],k[M]; 
int main(){
    scanf("%d%d%d%d",&n,&m,&v,&e);
    for (int i=1;i<=n;++i) scanf("%d",&c[i]);
    for (int i=1;i<=n;++i) scanf("%d",&d[i]);
    for (int i=1;i<=n;++i) scanf("%lf",&k[i]);
    for (int i=1;i<=v;++i) for (int j=1;j<=v;++j) dis[i][j]=1e9;
    for (int i=1;i<=e;++i) 
        scanf("%d%d%d",&x,&y,&z),dis[x][y]=dis[y][x]=min(dis[x][y],z);
    for (int i=1;i<=v;++i) dis[i][i]=0;
    for (int kkk=1;kkk<=v;++kkk)
        for (int i=1;i<=v;++i) if (i!=kkk)
            for (int j=1;j<=v;++j)
                if (i!=j&&j!=kkk) dis[i][j]=min(dis[i][kkk]+dis[kkk][j],dis[i][j]);
    for (int i=1;i<=n;++i) for (int j=0;j<=m;++j) f[i][j][0]=f[i][j][1]=1e9;
    f[1][0][0]=f[1][1][1]=0.00; f[1][1][0]=0.00;
    for (int i=2;i<=n;++i){
        int cc=dis[c[i-1]][c[i]],cd=dis[c[i-1]][d[i]],dc=dis[d[i-1]][c[i]],dd=dis[d[i-1]][d[i]];
        f[i][0][0]=f[i-1][0][0]+cc; 
        for (int j=1;j<=min(i,m);++j){
            f[i][j][0]=min(f[i-1][j][0]+cc,f[i-1][j][1]+cc*(1-k[i-1])+dc*k[i-1]);
            
            f[i][j][1]=min(f[i-1][j-1][0]+cd*k[i]+cc*(1-k[i]),
                           f[i-1][j-1][1]+cc*(1-k[i-1])*(1-k[i])+cd*(1-k[i-1])*k[i]+
                           dc*k[i-1]*(1-k[i])+dd*k[i-1]*k[i]);
        }
    }
    double ans=1e9;
    for (int i=0;i<=m;++i)
        ans=min(ans,min(f[n][i][0],f[n][i][1]));
    printf("%.2lf",ans);
}