BZOJ 4817数点涂色题解

题目链接

考试考了一道类似的题目，然后不争气的挂掉了，于是跑过来学习这道题的解法...

我还是太菜了....

我们可以发现任意时刻，原树中颜色相同的点的集合一定是一条链，

 

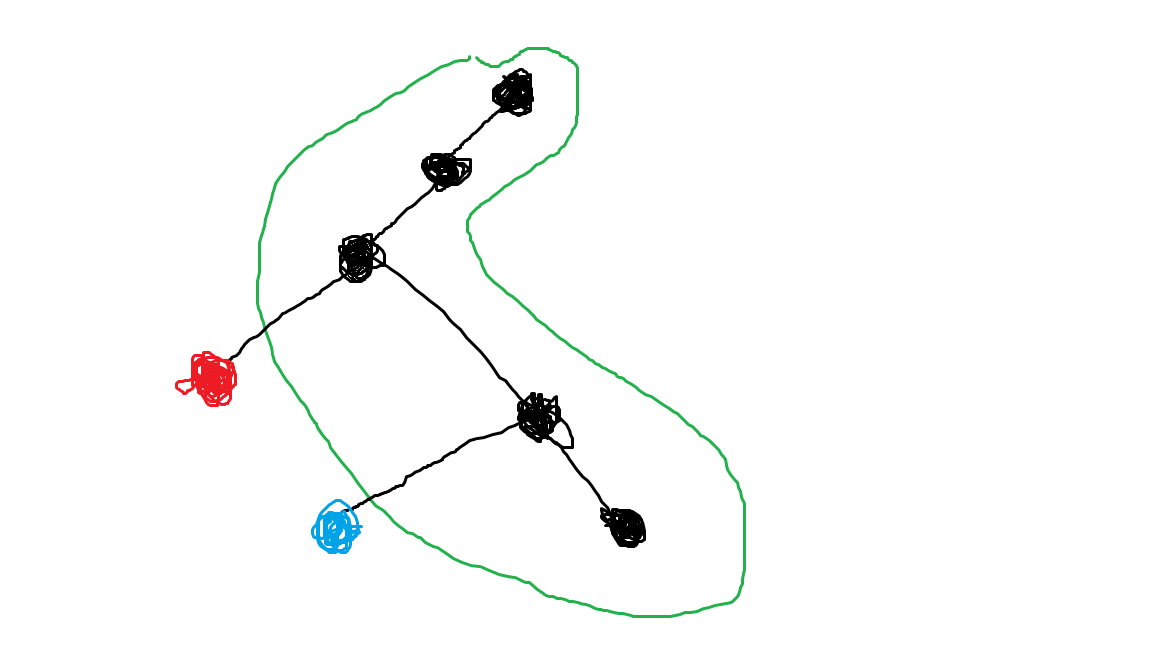
即上面这种状态，而这种结构是不是跟某种毒瘤数据结构很想，没错，就是LCT

我们发现LCT中的每一颗splay对应着每一段颜色的链

修改节点x到根的颜色时，只需要access一下就好了

我们再考虑每一次修改时对答案的影响

每一个节点到根的权值记作f[i]，显然f[i]就是i节点到根节点所经过的轻边数目加1

我们再利用一颗线段树维护dfs序上的f[]数组，方便查询

我们access是每次将虚边变为实边是就将那颗子树中的f[]数组减一

每次实边边虚边就加一

操作三的答案可以通过dfs序查询子树最大

而操作二的答案可很容易发现就是f[x]+f[y]-2*f[lca(x,y)]+1

一样维护一下就好了

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

const int mn = 1e5 + 10;
const int inf = 0x3f3f3f3f;

struct edge{int to,next;};
edge e[mn*2];
int head[mn],edge_max,n,m;
int mx[mn*4],tag[mn*4];
int fa[mn],in[mn],out[mn],deep[mn],id[mn],clo,siz[mn],bl[mn];

void add(int x,int y)
{
    e[++edge_max].to=y;
    e[edge_max].next=head[x];
    head[x]=edge_max;
}

void dfs(int x)
{
    siz[x]=1;
    in[x]=++clo;
    id[clo]=x;
    for(int i=head[x]; i; i=e[i].next)
    {
        if(e[i].to==fa[x]) continue;
        fa[e[i].to]=x;
        deep[e[i].to]=deep[x]+1;
        dfs(e[i].to);
        siz[x]+=siz[e[i].to];
    }
    out[x]=clo;
}

void dfs2(int x,int chain)
{
    bl[x]=chain;
    int k=0;
    for(int i=head[x]; i; i=e[i].next)
    {
        if(e[i].to!=fa[x] && siz[e[i].to]>siz[k])
            k=e[i].to;
    }
    if(!k) return ;
    dfs2(k,chain);
    for(int i=head[x]; i; i=e[i].next)
    {
        if(e[i].to!=fa[x] && e[i].to!=k)
            dfs2(e[i].to,e[i].to);
    }
}

int lca(int x,int y)
{
    while(bl[x]!=bl[y])
    {
        if(deep[bl[x]]<deep[bl[y]]) swap(x,y);
        x = fa[bl[x]];
    }
    if(deep[x]>deep[y]) swap(x,y);
    return x;
}

void updown(int cur)
{
    mx[cur]=max(mx[cur<<1],mx[cur<<1|1]);
}

void pushdown(int cur)
{
    if(tag[cur])
    {
        tag[cur<<1]+=tag[cur];
        tag[cur<<1|1]+=tag[cur];
        mx[cur<<1]+=tag[cur];
        mx[cur<<1|1]+=tag[cur];
        tag[cur]=0;
    }
}
void modify(int l,int r,int cur,int L,int R,int z)
{
    if(l>=L && r<=R)
    {
        tag[cur]+=z;
        mx[cur]+=z;
        return ;
    }
    if(l>R || r<L) return ;
    int mid=l+r>>1;
    pushdown(cur);
    modify(l,mid,cur<<1,L,R,z);
    modify(mid+1,r,cur<<1|1,L,R,z);
    updown(cur);
}
int query(int l,int r,int cur,int L,int R)
{
    if(l>=L && r<=R) return mx[cur];
    if(l>R || r<L) return -inf;
    int mid=l+r>>1;
    pushdown(cur);
    int ans;
    ans=max(query(l,mid,cur<<1,L,R),query(mid+1,r,cur<<1|1,L,R));
    updown(cur);
    return ans;
}
void build(int l,int r,int cur)
{
    if(l==r)
    {
        mx[cur]=deep[id[l]];
        return ;
    }
    int mid=l+r>>1;
    build(l,mid,cur<<1);
    build(mid+1,r,cur<<1|1);
    updown(cur);
}
struct LCT
{
    int fa[mn],c[mn][2];
    bool nroot(int x)
    {
        return c[fa[x]][0]==x || c[fa[x]][1] ==x;
    }
    void rotate(int x)
    {
        int y=fa[x],z=fa[y];
        int flag;
        if(c[y][0]==x) flag=1;
        else flag=0;
        if(nroot(y))
        {
            if(c[z][0]==y) c[z][0]=x;
            else c[z][1]=x;
        }
        c[y][flag^1]=c[x][flag];fa[c[y][flag^1]]=y;
        c[x][flag]=y;
        fa[y]=x,fa[x]=z;
    }
    void splay(int x)
    {
        while(nroot(x))
        {
            int y=fa[x],z=fa[y];
            if(nroot(y))
            {
                if((c[z][0]==y) ^ (c[y][0]==x)) rotate(x);
                rotate(y);
            }
            rotate(x);
        }
    }
    int findroot(int x)
    {
        while(c[x][0]) {
            x=c[x][0];
        }

        return x;
    }
    void access(int x)
    {
        int y=0;
        while(x)
        {
            splay(x);
            if(c[x][1])
            {
                int tmp=findroot(c[x][1]);
                modify(1,n,1,in[tmp],out[tmp],1);
            }
            if(y)
            {
                int tmp=findroot(y);
                modify(1,n,1,in[tmp],out[tmp],-1);
            }
            c[x][1]=y;
            y=x;
            x=fa[x];
        }
    }
}T;

int main()
{
    int opt,x,y,m;
    scanf("%d%d",&n,&m);
    for(int i=1; i<n; i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y),add(y,x);
    }
    deep[1]=1;
    dfs(1);
    dfs2(1,1);
    build(1,n,1);
    for(int i=1;i<=n;i++)
        T.fa[i]=fa[i];
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d",&opt,&x);
        if(opt==1)
            T.access(x);
        else if(opt==2)
        {
            scanf("%d",&y);
            int ans=0;
            ans=query(1,n,1,in[x],in[x]);
            ans+=query(1,n,1,in[y],in[y]);
            int z=lca(x,y);
            ans-=2*query(1,n,1,in[z],in[z]);
            ans++;
            printf("%d\n",ans);
        }
        else  printf("%d\n",query(1,n,1,in[x],out[x]));
    }
    return 0;
}