洛谷2375 BZOJ 3670动物园题解

题目链接

洛谷链接

我们发现题目要我们求的num[i]东西本质上其实是

求有多少以i结尾的非前缀且能与前缀匹配的字符串，而且要求字符串长度小于(i/2)

我们先不考虑字符串长度的限制，看所有以i结尾的非前缀且能与前缀匹配的字符串如何计数

考虑到KMP算法的next数组求解的过程,大家应该都想到i结尾的非前缀且能与前缀匹配的字符串的总数就是next[i]跳到0的所跳的次数

为什么是这样的呢?

如上图所示，其中绿色的串与红色的串是匹配的，若还要寻找匹配的串

不难发现所有以红色结尾处结尾所能匹配的串都是满足要求的

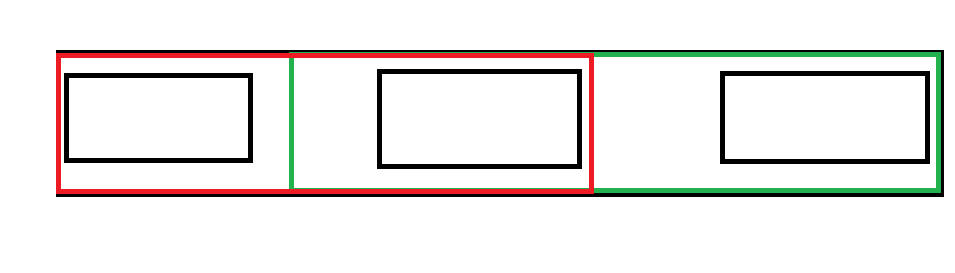
从上面的图不难发现以上结论是对的

具体求解时，我们先求一遍next数组，若next[i]为0,则不存在这样的字符串,如果大于0,则令num[i]=dep[next[i]]+1

但是我们还要考虑长度小于i/2这一个限制

一个朴素的想法就是next不停跳知道小于i/2为止，但这样复杂度是nlogn，TLE

所以我们要在做一遍魔改版KMP，求的是i结尾的非前缀且能与前缀匹配而且长度小于i/2的最长字符串

num[i]=dep[next2[i]]+1

魔改版KMP的求解过程与KMP类似,只是加了一句while(next[j]>i/2) j=next[j]

附上代码

# include<iostream>
# include<algorithm>
# include<cstring>
# include<cmath>
# include<cstdio>
const int mod = 1e9 + 7 ;
const int mn = 1100005;
int n,ans,N;
char s[mn];
int nxt[mn],dep[mn];
int main()
{
    int tmp;
    scanf("%d",&n);
    while(n--)
    {
        ans=1;
        scanf("%s",s+1);
        N=strlen(s+1);
        nxt[1]=0;
        dep[0]=0,dep[1]=1;
        for(int i=2,j=0;i<=N;i++)
        {
            while(j>0 && s[i]!=s[j+1]) j=nxt[j];
            if(s[i]==s[j+1]) j++;
            nxt[i]=j;
            dep[i]=dep[j]+1;
        }
        /*for(int i=1;i<=N;i++)
        printf("%d ",nxt[i]);*/
        for(int i=2,j=0;i<=N;i++)
        {
             while(j>0 && s[i]!=s[j+1]) j=nxt[j];
             if(s[i]==s[j+1]) j++;
             while(j>i/2) j=nxt[j];
             ans=1ll*ans*(dep[j]+1)%mod;
        }
        printf("%d\n",ans);
    }
    return 0;
}