无源汇有上下界可行流

Describe:

\(n\) 个点，\(m\) 条边，每条边 \(e\) 有一个流量下界 \(\text{lower}(e)\) 和流量上界 \(\text{upper}(e)\)，求一种可行方案满足流量守恒的同时满足每条边的限制条件。

Solution:

可以先考虑满足所有边的最低条件，获得一个初始的流量网络。

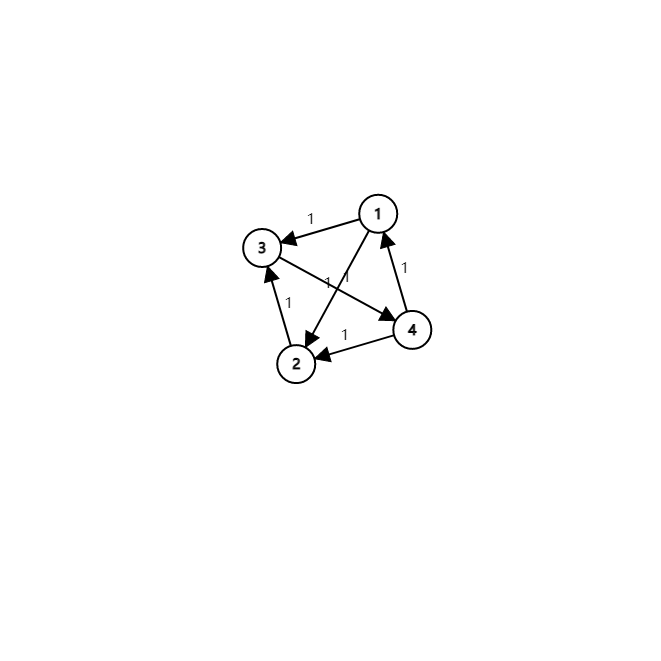
这时各个点是不一定满足流量守恒的。可能会有多余的流量无处可走，也可能会有流量不足以流出。因此可以建立一个源点，补充不足的流量，同时也建立一个汇点，汇入多余的流量。

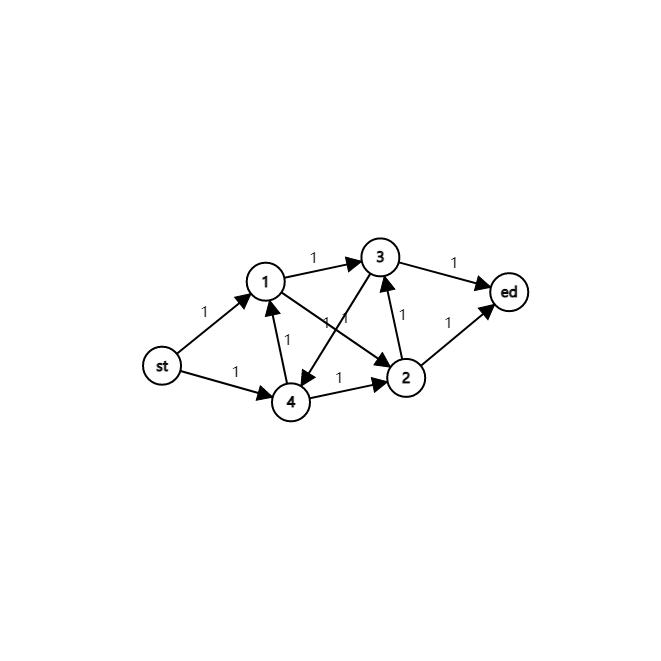
如果能在满足所有边的条件下从源点全部流入汇点，显然就是一个可行流。

因此可以建立一个残量网络，每条边的流量改为 \(\text{upper}(e) - \text{lower}(e)\)，跑一个最大流。判断一下最大流是否等于源点的流量即可。每条边的实际流量就是最低流量加残量网络中每条边流出的流量。

Code:

bool _Start;
#include<deque>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
namespace IO
{
	#define TP template<typename T>
	#define TP_ template<typename T,typename ... T_>
	#ifdef DEBUG
	#define gc() (getchar())
	#else
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	#endif
	#ifdef DEBUG
	void pc(const char &c)
	{
		putchar(c);
	}
	#else
	char pbuf[1<<20],*pp=pbuf;
	void pc(const char &c)
	{
		if(pp-pbuf==1<<20)
			fwrite(pbuf,1,1<<20,stdout),pp=pbuf;
		*pp++=c;
	}
	struct IO{~IO(){fwrite(pbuf,1,pp-pbuf,stdout);}}_;
	#endif
	TP void read(T &x)
	{
		x=0;static int f;f=0;static char ch;ch=gc();
		for(;ch<'0'||ch>'9';ch=gc())ch=='-'&&(f=1);
		for(;ch>='0'&&ch<='9';ch=gc())x=(x<<1)+(x<<3)+(ch^48);
		f&&(x=-x);
	}
	TP void write(T x)
	{
		if(x<0)
			pc('-'),x=-x;
		static T sta[35],top;top=0;
		do
			sta[++top]=x%10,x/=10;
		while(x);
		while(top)
			pc(sta[top--]^48);
	}
	TP_ void read(T &x,T_&...y){read(x);read(y...);}
	TP void writeln(const T x){write(x);pc('\n');}
	TP void writesp(const T x){write(x);pc(' ');}
	TP_ void writeln(const T x,const T_ ...y){writesp(x);writeln(y...);}
	TP void debugsp(const T x){fprintf(stderr,"%d ",x);}
	TP void debug(const T x){fprintf(stderr,"%d\n",x);}
	TP_ void debug(const T x,const T_...y){debugsp(x);debug(y...);}
	TP inline T max(const T &a,const T &b){return a>b?a:b;}
	TP_ inline T max(const T &a,const T_&...b){return max(a,max(b...));} 
	TP inline T min(const T &a,const T &b){return a<b?a:b;}
	TP_ inline T min(const T &a,const T_&...b){return min(a,min(b...));}
	TP inline void swap(T &a,T &b){static T t;t=a;a=b;b=t;}
	TP inline T abs(const T &a){return a>0?a:-a;}
	#undef TP
	#undef TP_
}
using namespace IO;
using std::cerr;
using LL=long long;
constexpr int inf=1e9,N=2e2+5,M=1e4+2*N;
struct edge
{
	int y,f,pre;
}a[M<<1];int alen=1,last[N];
void ins(int x,int y,int f)
{
	a[++alen]=edge{y,f,last[x]};
	last[x]=alen;
	a[++alen]=edge{x,0,last[y]};
	last[y]=alen;
}
int n,m,st,ed;
int w[M],in[N];
int h[N],cur[N];
bool pd()
{
	static std::deque<int>q;q.clear();
	q.push_back(st);
	memset(h,0,sizeof(h));h[st]=1;
	while(q.size())
	{
		int x=q.front();q.pop_front();
		for(int k=last[x];k;k=a[k].pre)
		{
			int y=a[k].y;
			if(a[k].f&&!h[y])
			{
				h[y]=h[x]+1;
				q.push_back(y);
			}
		}
	}
	return h[ed];
}
int findflow(int x,int f)
{
	if(x==ed)
		return f;
	int sx=0,sy;
	for(int &k=cur[x];k;k=a[k].pre)
	{
		int y=a[k].y;
		if(a[k].f&&h[y]==h[x]+1)
		{
			sy=findflow(y,min(a[k].f,f-sx));
			a[k].f-=sy;sx+=sy;
			a[k^1].f+=sy;
			if(sx==f)
				return sx;
		}
	}
	if(!sx)
		h[x]=-1;
	return sx;
}
int dinic()
{
	int s=0;
	while(pd())
	{
		memcpy(cur,last,sizeof(cur));
		s+=findflow(st,inf);
	}
	return s;
}
bool _End;
int main()
{
	// fprintf(stderr,"%.2 MBlf\n",(&_End-&_Start)/1048576.0);
	read(n,m);st=n+1;ed=st+1;
	for(int i=1;i<=m;i++)
	{
		int x,y,up,dn;
		read(x,y,dn,up);
		w[i]=dn;ins(x,y,up-dn);
		in[x]-=dn,in[y]+=dn;
	}
	int sum=0;
	for(int i=1;i<=n;i++)
		if(in[i]<0)
			ins(i,ed,-in[i]);
		else if(in[i]>0)
			ins(st,i,in[i]),sum+=in[i];
	if(dinic()==sum)
	{
		puts("YES");
		for(int i=1;i<=m;i++)
			writeln(w[i]+a[i<<1|1].f);
	}
	else
		puts("NO");
	return 0;
}