网络流24题 P2764 最小路径覆盖问题

思路

问题模型：有向无环图最小路径覆盖

转化模型：网络最大流

最小路径覆盖 = 点的总数 - 网络最大流。

思路大多来自课件，采用了拆点思路，如下方式建图:

对于原图中的每个点 \(x\) ，建两个点 \(x\) 和 \(x′\) 。
对于原图中的每一条边 \((i, j)\) ，从 \(i\) 向 \(j′\) 连一条边。
对这个图跑网络流求二分图匹配，求最大流期间记录路径，如果连出去的点不是起点，就当做这一条路的下一个点

来一张比较直观的建图之后的图（感谢洛谷，侵删）：

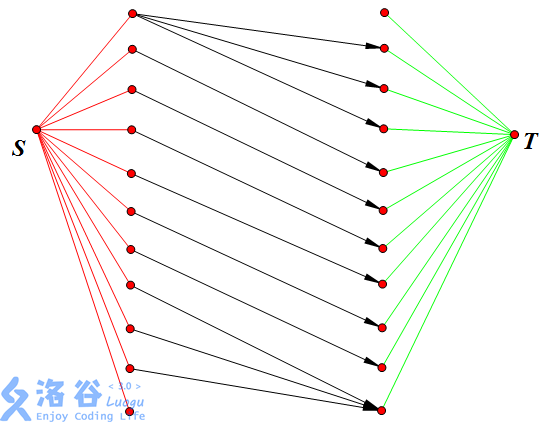
对于每个点 \(i\)：
\(i\) 只会匹配一次，则只会有一条形如 \((i, j)\) 的边被选择；
\(i′\) 只会匹配一次，则只会有一条形如 \((j, i)\) 的边被选择；
故选择的一定是若干条不相交简单路径。
如果一个点 \(i\) 没有匹配，则其必为某条路径的结尾。
所以最后的答案就是 \(n-\) 匹配数。

数据不是很强，\(\text{Dinic}\) 不加优化也能过

代码

#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 1e5 + 11;
const int B = 1e3 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar();
  int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, m, s, t, cnt = 1, ans;
int dep[A], head[A], inq[A], vis[A], net[A];
struct node { int to, nxt, val; } e[A];

inline void add(int from, int to, int val) {
  e[++cnt].to = to;
  e[cnt].val = val;
  e[cnt].nxt = head[from];
  head[from] = cnt;
}

inline bool bfs() {
  queue <int> Q;
  memset(dep, inf, sizeof(dep));
  Q.push(s), dep[s] = 0, inq[s] = 1;
  while (!Q.empty()) {
    int x = Q.front(); 
    Q.pop(), inq[x] = 0;
    for (int i = head[x]; i; i = e[i].nxt) {
      int to = e[i].to;
      if (dep[to] > dep[x] + 1 && e[i].val) {
        dep[to] = dep[x] + 1;
        if (!inq[to]) inq[to] = 1, Q.push(to);
      }
    }
  }
  if (dep[t] != inf) return 1;
  return 0;
}

int dfs(int x, int flow) {
  int tmp = 0;
  if (x == t) return flow;
  for (int i = head[x]; i; i = e[i].nxt) {
    int to = e[i].to;
    if (dep[to] == dep[x] + 1 && e[i].val) {
      if (tmp = dfs(to, min(flow, e[i].val))) {
        e[i].val -= tmp, e[i ^ 1].val += tmp;
        net[x] = to; //记录路径 
        if (x) vis[to - n] = 1; 
        //to一定是右边的点，且被走了，不是出发点 
        return tmp;
      }
    }
  }
  return 0;
}

int main() {
  n = read(), m = read(), s = 2 * n + 1, t = 2 * n + 2;
  for (int i = 1; i <= n; i++) add(s, i, 1), add(i, s, 0);
  for (int i = n + 1; i <= 2 * n; i++) add(i, t, 1), add(t, i, 0);
  for (int i = 1; i <= m; i++) {
    int x = read(), y = read();
    add(x, y + n, 1), add(y + n, x, 0);
  }
  int now = 0, ans = 0;
  while (bfs())
    while (now = dfs(s, inf)) ans += now;
  for (int i = 1; i <= n; i++) {
    if (!vis[i]) { //是一条路的出发点 
      int cur = i; 
      cout << cur << " ";
      while (net[cur] != t && net[cur] != 0) 
        cout << net[cur] - n << ' ', cur = net[cur] - n; 
        //不减 n 会出错，net一定是右方点 
      puts("");
    }
  }
  cout << n - ans << '\n';
  return 0;
}