「笔记」线段树

写在前面

大概是笔记吧
部分内容引用了$\texttt{OI-Wiki}$和【AgOHの数据结构】主席树
部分图片出处：【AgOHの数据结构】主席树
感谢 LuckyBlock 同学提供了例3、例12 和例15 的链接
如果有题目链接或者文章出现了错误，欢迎指出！

基本区间操作

单点修改，区间询问：对于每个线段树上的区间维护一个区间的信息之和

$eg.$单点修改，询问区间和，区间最大值
区间修改，单点询问：每次修改时对区间打上一个修改表及，在询问和修改时，一旦访问到一个区间，就将他的标记下传

$eg.$区间加，求单点的值

例题

线段树与标记下传

区间修改区间询问的线段树实现的重点：

标记之间的合并
区间信息之间的合并
区间信息与标记的合并

只要能快速地进行以上三个操作，理论上标记和区间信息可以是任何东西（划重点！），甚至是平衡树

权值线段树

权值线段树就是对一个值域上值的个数进行维护的线段树

举个例子，对于$1,2,2,3,4,4,5,5,6,7,8,8$，他的权值线段树就是

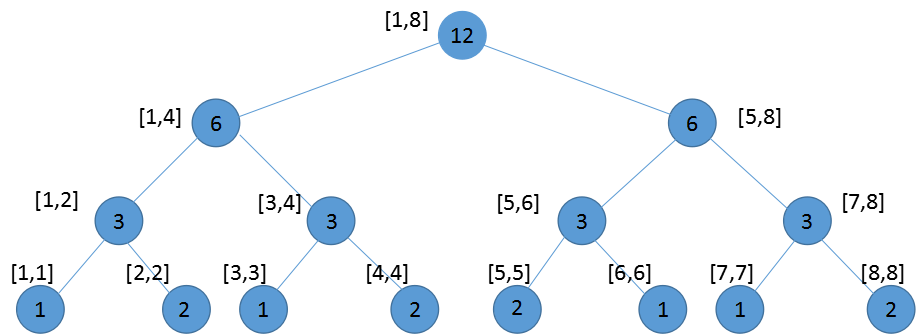
其中中括号内是值域，圆圈内表示的是值在对应值域里的数的个数

线段树合并

线段树合并其实就是动态开点权值线段树合并

动态开点：就是用哪个地方就开哪个地方，每次访问之前看看是否为空，为空就新建一个节点。询问时如果遇到没有开过点的点，就直接返回即可，时间复杂度是$\log n$的

普通的静态线段树左儿子为$rt<<1$，右儿子为$rt<<1|1$，用的空间大概是$4n$，动态开点线段树中左右儿子是不定的，要根据实际情况判断

为什么要用动态开点呢？因为有些时候是不能用静态线段树的，比如说：

值域很大

比如$10^9$，然而真正有效的点其实是很少的

（当然，离散化牛逼
可持久化

有$n$个线段树$T_1,T_2...T_n$，如果静态开空间当然是开不下的，但是如果它和主席树一样，$T_i$是在$T_{i-1}$的基础上进行修改的，就可以用可持久化的方法进行动态开点

两个可重集合合并的方法

假设有两个集合$S,T$，假设为了维护它们的信息，已经建好了两棵线段树$A_S,A_T$，现在要合并这两个区间，应该如何合并呢？

启发式合并

如果$|S|<|T|$，那么就枚举$S$中的元素，将其加到$T$的线段树中

小的合并到大的上，复杂度$O(n\log^2n)$，比较低效
线段树合并

根据线段树 美妙的结构：如果下标相同，那么两棵线段树的结构就会完全相同

设当前合并的节点为$X,Y$，区间为$[L,R]$，用$merge(X,Y,L,R)$实现合并，考虑如何实现
- 如果$X$为空，则返回$Y$
```
if (X == NULL) return Y;
```
- 如果$Y$为空，则返回$X$
```
if (Y == NULL) return X;
```
- 如果$L=R$，即为叶节点，直接将两点$sum$相加
```
if (L == R) {
  int z = newnode();
  sum[z] = sum[X] + sum[Y];
  return z; //合并的结果是z
}
```
- 否则新建节点$z$，分左右子树合并
```
int z = newnode(), mid = L + R >> 1;
lson[z] = merge(lson[X], lson[Y], L, mid);//左子树
rson[z] = merge(rson[X], rson[Y], mid + 1, R);//右子树
update(z);//从子树中获得信息
return z;
```
以上就是线段树合并的实现和伪代码。复杂度为$O(n\log n)$，证明：

以上的执行过程中，其实只有两种情况
- $X,Y$中有一个为$NULL$
  
  直接返回，复杂度$O(1)$
- $X,Y$都不为$NULL$
  
  单次执行过程复杂度为$O(1)$（只是单次）
  
  单次执行的过程中新建了一个节点，去掉了两个节点，总共相当于去掉了一个节点，所以执行总次数就是$O(\text{线段树点个数})$级别的
  
  一开始线段树中的节点数是$O(n\log n)$级别的，所以均摊下来总复杂度就是$O(n\log n)$级别

可持久化线段树

原理

关于可持久化数据结构的介绍，去看OI-Wiki

可持久化线段树是一种可持久化的数据结构，其特点是：在更新时，可持久化线段树尽可能与之前某一个版本共用一部分结点，从而起到节省空间的作用。

如下图，现在有一颗有7个节点的线段树

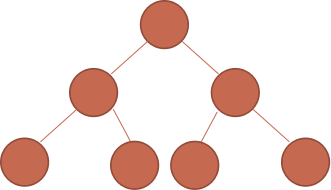
我们想要对图中的红点进行单点修改（其实就是单点修改，红点是包含它的区间）

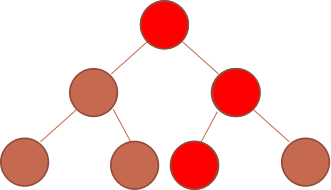
朴素的做法是建一棵新的线段树，但是这样十分浪费空间，因为线段树一次修改只会修改$\log$个节点，为了修改这$\log$个节点而去重新建一棵线段树是非常不可取的。

因此我们可以只去新建这$\log$个节点，并将新建的节点连接到原线段树中要修改的点连接的位置上，如下图

这样就大大节省了空间。

实现

见此题洛谷 P3919 【模板】可持久化线段树 1（可持久化数组）

/*
Author:Loceaner
*/
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define lson t[x].l
#define rson t[x].r
#define lc t[pre].l
#define rc t[pre].r
using namespace std;

const int A = 1e6 + 11;
const int B = 1e6 + 11;
const int mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;

inline int read() {
  char c = getchar(); int x = 0, f = 1;
  for ( ; !isdigit(c); c = getchar()) if (c == '-') f = -1;
  for ( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
  return x * f;
}

int n, m, a[A], cnt, num, rt[A];
struct tree { int l, r, w; } t[A * 20];

void build(int &x, int l, int r) {
  x = ++num;
  if (l == r) { t[x].w = a[l]; return; }
  int mid = (l +r) >> 1;
  build(lson, l, mid), build(rson, mid + 1, r);
}

void update(int &x, int pre, int l, int r, int pos, int val) {
  x = ++num, lson = lc, rson = rc;
  if (l == r) { t[x].w = val; return; }
  int mid = (l + r) >> 1;
  if (pos <= mid) update(lson, lc, l, mid, pos, val);
  else update(rson, rc, mid + 1, r, pos, val); 
}

int query(int x, int l, int r, int k) {
  if (l == r) return t[x].w;
  int mid = (l + r) >> 1;
  if (k <= mid) return query(lson, l, mid, k);
  return query(rson, mid + 1, r, k);
}

int main() {
  n = read(), m = read();
  for (int i = 1; i <= n; i++) a[i] = read();
  build(rt[0], 1, n);
  while (m--) {
    int k = read(), opt = read(), pos, val, x;
    if (opt == 1) pos = read(), val = read(), update(rt[++cnt], rt[k], 1, n, pos, val);
    else if (opt == 2) x = read(), rt[++cnt] = rt[k], cout << query(rt[cnt], 1, n, x) << '\n';
  }
  return 0;
}

例题集合

例题1

给定序列$a[1...n]$，$Q$次询问，要求支持：

区间乘-1

求区间最大字段和

$n,Q\le 10^5$

由上面重点中所说，我们最重要的就是解决以下三个问题

tag+tag
区间+区间
区间+tag

tag+tag

容易想到$tag$标记的就是区间是否乘$-1$
维护一个$bool$值，表示是否乘$-1$，如果乘了偶数次就相当于没乘

区间+区间

要维护区间的最大子段和$ans$，不仅要维护值，还要维护左右端点
合并两个子区间时，假设左子区间为$L$，右子区间为$R$，那么最大子段和的合并有以下三种情况：

$L$的最大子段和
$R$的最大子段和
跨越$L$和$R$的最大子段和

对于这种情况可以分成两部分，一个是$L$的后缀，另一个是$R$的前缀，因此还要维护区间的最大后缀和$suf$和最大前缀和$pre$

答案就是$\max\{L_{ans},R_{ans},L_{suf}+R_{pre}\}$

考虑如何更新最大后缀和和最大前缀和，以最大后缀和为例，两个子区间合并时，最大后缀和有两种情况：

右子区间的最大后缀和$R_{suf}$
右子区间的和$R_{sum}$+左子区间的最大后缀和$L_{suf}$

因此我们还需要维护区间的和$sum$
合并时最大前缀和同理，有 左子区间的最大前缀和$L_{pre}$ 和 左子区间的和$L_{sum}$+右子区间的最大前缀和$R_{pre}$ 两种情况

综上我们要维护$sum,ans,pre,suf$四个值以及端点

区间+tag

当区间乘了$-1$时，$sum$可以直接变为相反数，但是其他三个值并不能直接这么干

考虑区间乘$-1$时，最大字段和的变化

最大子段和会变成负的最小字段和
负的最小字段和会变成最大子段和

因此我们在维护最大字段和、最大前缀、最大后缀时，要维护同一套的最小字段和、最小前缀、最小后缀，在乘$-1$时，直接将两者交换，再乘$-1$即可

还有一些细节的地方，在此不再赘述（因为我也不会写也没有提交的地方（手动滑稽……然后这道题就做完了

SPOJ有几道题和这题挺像，但是忘记叫啥名字了

例题2

给定序列$a[1...n]$，支持单点修改，每次求区间单调栈大小

$n,Q\le 10^5$

区间单调栈是什么呢？对于一个区间，建立一个栈，首先将第一个元素入栈，从左往右扫，如果当前元素大于等于栈顶元素，就将其入栈，由此形成的栈即为单调不减的区间单调栈。

转化一下，其实就是求区间内满足$a[i]=\max\limits_{j=1}^ia[j]$的$a[i]$的个数。

一个自然的想法是维护单调栈的大小$siz$，那么如何去进行区间的合并呢？

合并两个子区间时，假设左子区间为$L$，右子区间为$R$，考虑合并之后的单调栈的组成部分：

第一部分：$L$的单调栈

因为单调栈是从左往右做的，所以$L$的单调栈必然是大区间单调栈的一部分
剩余部分

设出函数$calc(now,pre)$，$now$表示当前节点，$pre$表示当前单调栈的栈顶，$calc$函数计算剩余部分的单调栈的大小

总的单调栈大小$siz$就是$L_{siz}+calc(R,L_{max})$

calc的实现

现在有$calc(now,pre)$，$l$表示$now$的左子树，$r$表示$now$的右子树

如果$pre>l_{max}$，说明整个左子区间都不用考虑了，此时答案就变成了$calc(r,pre)$
如果$pre\le l_{max}$，此时$l$是有贡献的，他对$siz$的贡献就是$calc(l,pre)$，右子树的贡献为$calc(r,l_{max})$，总贡献就是$calc(l,pre)+calc(r,l_{max})$

至此$calc$就推完了，但是我们发现如果仅仅是这样的话，在最坏的情况下，复杂度会爆炸，那么怎么优化呢？

观察$calc(r,l_{max})$，发现它就等于$siz-l_{siz}$，所以第二种情况就可以变成$calc(l,pre)+siz-l_{siz}$，其中$siz$都是可以处理好的

这样我们就可以在$O(\log n)$的时间里完成一次合并

总时间复杂度$O(Q\log^2 n)$

原题：洛谷 P4198 楼房重建

例题3

有一个序列$a[1...n],$每个$a[i]$是$(c,x,y)$，表示颜色和坐标

现在支持单点修改以及区间询问：颜色不同的曼哈顿距离最大的一对点的距离

$n,Q\leq10^5$

这个题其实就是一堆普通的处理的小技巧叠加起来

曼哈顿距离：设坐标系中两点的坐标为$(x_1,y_1)$、$(x_2,y_2)$，则$|x_1-x_2|+|y_1-y_2|$就是两点之间的曼哈顿距离

简单的小技巧就是把它拆成四个部分，如下

\[\max\begin{cases}x_1-x_2 + y_1-y_2\\x_1-x_2 +y_2-y_1\\x_2-x_1+y_1-y_2\\x_2-x_1+y_2-y_1\end{cases} \]

显然这四种的最大值就是曼哈顿距离，所以分情况讨论，讨论每种情况下颜色不同的曼哈顿距离最大的一对点的距离，最后取最大值，就是我们要的答案了

以第一种为例，其实可以写成$(x_1+y_1)-(x_2+y_2)$，这就相当于每个点有了一个权值$w=x+y$，那么现在的问题就相当于找权值最大和权值最小的点，而且他们的颜色要不同

如果不考虑颜色不同，我们就可以用线段树直接维护区间权值的最大值和最小值

那么如果考虑颜色不同该怎么做呢？一种不太显然的做法是：在维护最大值和其颜色的同时，维护一个次大值以及其颜色，保证最大值和次大值的颜色不同，在维护最小值和其颜色的同时，维护一个次小值以及其颜色，保证最小值和次小值的颜色不同

当区间最大值和最小值颜色不同时，答案就是两者之差，当两者颜色相同时，有 最大值-次小值 和 次大值-最小值 两种情况，两者颜色一定不同，所以取$\max$即可

颜色不同的次权值如何维护？

假设现在已经知道了左子区间的最大值、次大值及其颜色，右子区间的最大值、次大值及其颜色，那么新区间的最大值一定为两个子区间种的最大值之一，次大值的话其他三个值都有可能，选出其中最大的且与最大值颜色不同的一个即可

其他三种情况也可以类似的处理

这样的话这个题就做完了，直接开四棵线段树就好

原题链接https://codeforces.com/gym/101955/problem/E

技巧总结

对曼哈顿距离的处理
对颜色不同的处理

例题4

给定$a[1...n]$，要求支持单点修改，以及区间询问$a[l...r]$不能组成的最小的数

$n,Q\le2\times10^5,1\le a[i]\le10^9$

时限$15s$

听老师说十五秒直接三个$log$就能艹过了

首先一定要有一个值为$1$的数，否则最小的不能组成的数就是$1$

小结论

假设现在可以表示$1\sim x$中的所有数，这个时候如果来了一个值为$x+1$的数，那么我们就可以表示出$1\sim 2x+1$

这是比较显然的，因为$1\sim x$都可以表示出来，$x+1$有了，之后的$x+2\sim 2x+1$就可以直接用$x+1$和之前的数拼起来了

推广一下，如果现在已经可以表示出$1\sim x$中的所有数，如果来了一个值为$y$的数，且$y\leq x+1$，那么我们就可以拼出$1\sim x+y$中的数

假设$T$表示能表示出$1\sim T$，那么只要加入一个$\leq T+1$的数，$T$的范围就会大大增加，所以就可以扩展到区间里$\le T+1$的数和

要用有鼠撞树卒的主席树维护对于一个二维区间里$\leq T+1$的数的和

我不会了，爬

例题5

给定$a[1…n]$要求支持：

区间加

区间变成$max(a[i]+v,0)$，$v$可以是正数也可以是负数

求单点当前值

求单点历史最大值

区间覆盖

$n,Q\le10^5$

他跳了

例题6

给定序列列$a[1…n]$，要求支持区间和以及让$a[L…R]$对$x$取$\min$
$n,Q\le10^5$

他跳了

例题7

给定序列$a[1...n]$以及$k,d$，求一个最长的区间，使得最多加入$k$个数之后，排序得到的是一个公差为$d$的等差数列

$n\le2\times10^5$

要素察觉：必须要是一个公差为$d$的等差数列

首先要特判掉$d=0$的情况，这样的情况下就是要寻找最长的一段数字相同的区间

那么再来看别的情况，对于一个区间$[l,r]$：

这个等差数列里的所有数$\bmod d$的结果应该一样
区间内没有重复的数

考虑怎么进行

首先将序列分成若干个$x \bmod d$都一样的子区间

在从左往右扫的过程中，如果遇到了与前面$x\bmod d$的值不同的数，就将左边$x\bmod d$值相同的数作为一个独立的区间来处理，最后就可以分成若干个$x \bmod d$都一样的子区间
对于一个满足$x\bmod d=c$的数列，把所有的$x$变成$\dfrac{x-c}{d}$（因为整形的性质，可以直接除），这样整个序列的公差就为$1$了，问题就转化成了加入$k$个数，使区间$sort$后公差为$1$。(归一化)
对于一个区间$[L,R]$，考虑如何算出最少加几个数
- 首先不能有重复
- 显然最少加的数的个数就是$\max(L,R)-\min(L,R)+1-(R-L+1)$
从小到大枚举$R$,相当于求最小的$L$,使得
- $[L,R]$无重复
  
  从小到大枚举$R$,对于新的$a[R]$很容易知道它前面一个和他相等的数$a[T]$（可以用$map$实现），那么$L$至少要大于$T$
- $\max(L,R)-\min(L,R)+1-(R-L+1)\le k$
  
  即$\max(L,R)-\min(L,R)+L\le k + R$
  
  用线段树维护$w[L]=\max(L,R)-\min(L,R)+L$
  
  假如$L$的下界是$T$，那么我们要在$[T+1,R]$中找最左的位置使得$w\le k + R$

如何维护$w$？用单调栈。维护一个单调递减的栈，因为单调栈递减的性质，所以当一个大于栈顶的元素加入时，会不断地弹出栈顶，直到栈顶元素大于此元素为止，再将此元素入栈。

此处，单调栈可以将$\max(L,R)$分成递减的若干段，考虑如何实现：

如图所示，假设有一个单调递减的单调栈，其中$S1> S2> S3$，$S3$为栈顶元素

ddz1

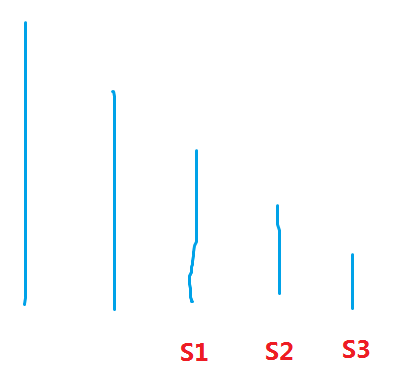
由于单调栈的性质，$S1$和栈中上一个元素之间可能是有别的元素的，所以$S1,S2,S3$其实是代表了三个区间的最大值

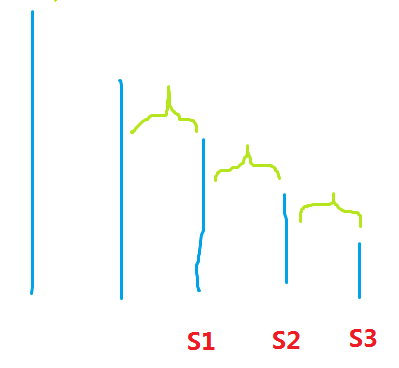
此时，单调栈中来了一个新的元素$a$，显然$a>S1>S2>S3$，所以我们要将$S1,S2,S3$弹栈

ddz2

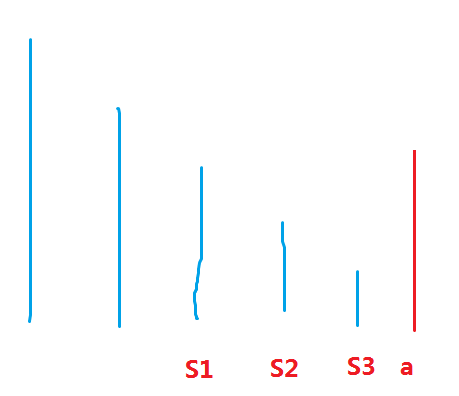
在弹栈时，因为此时这三个元素的值不能代表这三个绿色段的最大值了，所以我们需要将三个段的贡献从线段树中减去

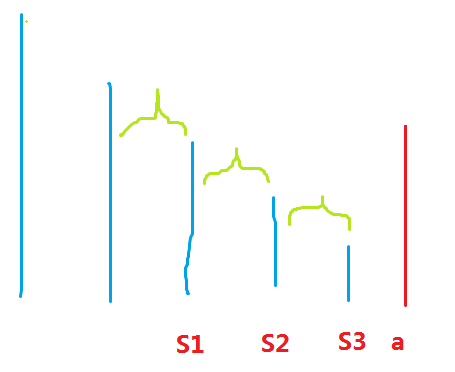
同时，新的元素$a$就加进来了，这个时候就可以发现原来三个段的代表元素被弹出之后，其实就被新元素所接管了，所以再对一整个区间进行区间加操作即可

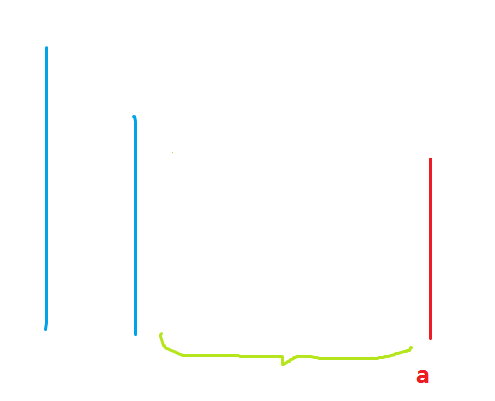
这样单调栈就实现了将$\max(L,R)$分成了递减的若干段，由此就可以不断进行段树的区间加、区间减。

$\min$的维护同理。

最后再调用一下找最左边的$w\le k+R$的算法就好了。

总时间复杂度$O(n\log n)$

原题：CF407E

例题8

给定序列$a[1...n]$，$Q$次询问$a[L...R]$中$L\le i\le R，L\le j\le R$且$i\ne j$时$|a_i-a_j|$ 的最小值

$n,Q\le2\times10^5$

维护区间的一种比较通用的处理方法：

从小到大枚举$R$，维护一颗线段树，$w$的下标$L$表示$L\sim R$的答案，每次$R+1$时做一些修改

好处：每次只需考虑新的数

假设现在有一个$a$序列，枚举右端点从$R-1$转移到了$R$，设寻找的一个数为$x$

那么可以从两个方面考虑：

$x>a[R]$

从$R$开始向左寻找比$a[R]$大的最近的数$a[x]$，由此可以得出$L=1\sim x$有一个新的备选的值：$a[x]-a[R]$，取$\min$即可

但这是不够的，我们需要继续往左寻找新的数，假设为$a[y]$

那么$a[y]$首先必须满足的条件就是$a[R]\le a[y]\le a[x]$，否则一定不会更新答案，此时他就会造成一个$a[y]-a[R]$的影响，同时还有一个影响就是$a[x]-a[y]$，这个影响其实在右端点枚举到$x$时就已经统计过了，所以如果$a[y]-a[R]$已经比$a[x]-a[y]$大的话，就没有更新的必要了，所以$a[y]-a[R]<a[x]-a[y]$

所以$y$满足的条件为$y< x,a[y]\in[a[R],\dfrac{a[R]+a[x]}{2}]$，且$y$最大

这个东西可以用主席树维护：线段树用权值线段树，维护一下在这个权值区间里下标最大的数，查询时查询一下主席树在$x$时的历史信息。

找到$y$之后，就用$a[y]-a[R]$去更新$w[1...y]$

之后再找$z$，同上要满足的条件是：$a[z]-a[R]<a[y]-a[z]$

所以$a[z]\in[a[R],\dfrac{a[R]+a[y]}{2}]$

之后一次次寻找，最多找$\log$次
$x<a[R]$

做法同上。

做……完……了……

原题：CF765F

例题9

给定$n$，定义$work(x,y)$等于$[1,n]$的线段树上对$[x,y]$进行区间询问后访问到的点的个数

给定$L,R$,求$work(i,j)$的和，其中$L\le i\le j\le R$

$n,Q\le 10^5$

考虑$work(x,y)$如何快速求

对于线段树上一个点$[L,R]$，被访问到的条件有：

与$[x,y]$有交
$[x,y]$不包含$[fa_L,fa_R]$（$fa$表示父亲节点）

假设现在的询问是$[X,Y]$，那么要求的就是

\[ans=\sum\limits_{i=X}^{Y}\sum\limits_{j=i}^Ywork(i,j) \]

如果$X,Y$包含了父区间

设$C(len)=\dfrac{len\times(len+1)}{2}$

那么首先要去掉的就是与$L,R$不交的区间：$C(L-X)+C(Y-R)$

第二步取出的是虽然与有交，但是包含了父亲区间即：$(fa_L-X+1)(Y-fa_R+1)$

最后答案是$C(Y-X+1)-[C(L-X)+C(Y-R)]-(fa_L-X+1)(Y-fa_R+1)$
如图所示

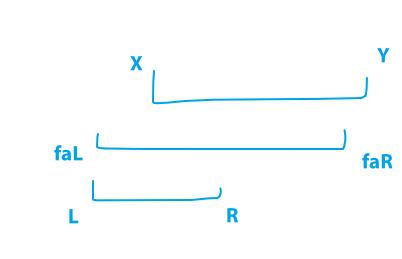
这样的情况就是$C(Y-X+1)-C(Y-R)$
其他同理，分析一下即可

这样的复杂度是$O(nQ)$的，如何优化呢？

$C(Y-X+1)-[C(L-X)+C(Y-R)]-(fa_L-X+1)(Y-fa_R+1)$展开其实就是一个二次函数，是可以预处理的

听不懂了

爬。。有空再补

此题总结

$work(x,y)$
$O(nQ)$
对$O(nQ)$剪枝，卡常数
某些情况整个子树可一起算

例题10

有$Q$次操作，每次给定$L,R,K,B$：对于$L<=i<=R $令$a[i]=\max(a[i],K\times i+B)$，单点询问$a[i]$

$n,Q\le10^5$

显然$K\times i + B$是一条线段，所以每次我们要加一条线段进去，就像下面这样

~~一个想法是把线段视为一个tag，打到线段树上去，但是显然是不能这么做的，因为线段在某些情况下无法合并（或很难合并），如下图~~

其实这题就是李超线段树模板了

$addline(rt,line)$表示往$rt$上插一条线段$line$，分类讨论一下，无论如何进行，最后都会变成$addline(child,line)$的形式，所以给一个区间加一条线段的最坏复杂度为$O(\log n)$，又因为是对线段树的区间加直线，所以会给$\log$个区间进行$addline$操作，所以每次修改的总复杂度就是$O(\log^2 n)$

实现时需要记录线段左端点、右端点和区间$mid$时线段的值，然后根据原来线段这三个点的大小和现在的线段这三个点的大小进行比较。

例题11

定义$\min-\max$树是一颗二叉树，每个叶子节点有一个权值，权值互不相同

现在定义每个非叶子的权值为：有$p$的概率是两个儿子的权值的$max$，有$1-p$的概率是两个儿子的权值的$min$

对于所有可能的$i$，输出根节点权值为$i$的概率

$n\le5\times10^5$

概率不会，跳了

与线段树合并有关

例题12

给定一棵$n$个点的树，点有颜色，每次询问点$x$子树内距离$x $ 不超过$d$的点有多少种不不同的颜色
$n\le10^5$

无内鬼（他忘记出处）（某个群友提供了出处但是找不到记录/kk

问题可以转化为寻找不同颜色的$y$的个数，$y$满足$y\in x$的子树且$dep[y]\le dep[x]+d$

对树上每个点开一个线段树$ans[x]$，用$ans[x][i]$表示在$x$的子树中有几种颜色深度最小是$i$，假如能够求出，那么最后的答案就是$\sum\limits_{i=1}^{dep[x]+d}ans[x][i]$

那么怎么做呢？

假设$x$节点有两个儿子$y,z$，一个简单又粗暴的想法是直接用$ans[x]=merge(ans[y],ans[z])$，但是这样显然是不太合理的，因为可能有些颜色在$y$中出现，同时也在$z$中出现

其实这个东西是可以用的，但是还需要进行一些处理，我们记它为$DA[x]=merge(ans[y],ans[z])$，这个东西也有一个比较好的性质，就是重复的颜色刚好被算了两次（为什么不会是三次，我觉得如果从下往上合并次数多了就会大于两次啊……还是说他说的就只是指这一次合并啊？当然如果在底层处理好的话也没啥问题了，求gyh解答）

我们要想办法把这种影响给消除掉，比如说有一种颜色在$y$中的最小深度是$y_1$，在$z$中的最小深度是$z_1$，因为算重，会导致$DA[x][y_1]++,DA[x][z_1]++$，我们要想办法把$y_1$和$z_1$之中深度比较大的那个减掉（为什么是较大的，较小的不行嘛？求gyh证明），比如说$z_1$比$y_1$大，那么就把$DA[x][z_1]--$，只要能把所有的这样的$z_1$消除影响，最后得出的答案其实就是我们想要的答案了

那我们要知道被多算的颜色是什么，而且要枚举每个被多算的颜色，因为我们对于每个被多算的颜色要在线段树上进行一些修改。

考虑线段树合并，对于$y$和$z$建立以颜色为下标的线段树$c[y],c[z]$，合并的时候将这两棵线段树合并，即$merge(c[y],c[z])$，那么当我们合并到叶子节点$i$时，说明叶子节点上的这种颜色$i$就刚好是在两棵线段树中都出现的颜色（非常巧妙$qwq$）

但是我们该怎么删呢？$c[y][i]$记录$i$在$y$的子树中最小深度是什么，在合并到叶子节点时，这种颜色分别对应$c[y][i]$和$c[z][i]$，其实就是上面我们说的$y_1,z_1$，找出深度较大的，在线段树中进行单点修改把它删掉，就完成了修改。

复杂度$O(n\log n)$，证明：

有两种线段树$ans[x],c[x]$，算法步骤：

合并$ans[x]$
合并$c[x]$

合并时在叶子节点处会进行单点删除，每次是$O(\log n)$的

看起来好像是两个$log$，但其实是叶子节点之后$O(n)$个（可以理解成每个叶子节点都对应着原先树上的某一个节点），每次这样合并会减少一个叶子节点，每次减少时会有$O(\log n)$的复杂度，所以总的复杂度就是$O(n\log n)$

星星星

$ans[x][i]$表示$x$子树内最小深度为$i$的颜色个数

$c[x][i]$表示颜色$i$在$x$子树内的最小深度

这道题运用了线段树比较神奇的性质

一定不会有重复的叶子节点，如果一个颜色在这个子树中有，在另一个子树中没有，那么在动态开点时另一个子树中一定不会开出这个叶子节点

原题链接：七彩树

例题13

给定数组 $a[1…n]$，一开始都为$1$，要求支持以下三种操作：

给定$L,R$，对于$L\le i\le R$，令$a[i]=\varphi(a[i])$

给定$L,R,x$，对于$L\le i\le R$，令$a[i]=x$

求区间和

$n,Q\le 10^5,x\le 10^7$

当没有操作2时，做法还是比较显然的

有引理：

一个奇数$x$的欧拉函数$\varphi(x)$必定是一个偶数

根据欧拉函数的定义有：

\[\varphi(x)=x\prod\dfrac{p_i-1}{p_i} \]
其中$p_i$是$x$质因数分解后得到的的质因子。

因为$x$是奇数，所以质因数分解得到的每一个质因子也一定是奇数，因此$p_i-1$一定是偶数，又因为在分母上的$p_i$相乘的结果一定是$x$的因子，所以答案就是若干个偶数相乘或者一个奇数和若干个偶数相乘，得到的结果一定是偶数。
一个偶数的$x$的欧拉函数$\varphi(x)$一定小于等于这个数的一半

和偶数互质的数一定是奇数，不然就会有共同的因子$2$，因为偶数都是$2$的倍数，而小于$x$的正奇数不超过$\dfrac{x}{2}$个，所以$\varphi(x)\le \dfrac{x}{2}$

所以一个数最多进行$\log$次操作1就会变成$1$，如果一个区间全部是$1$了就可以直接跳过，否则就往下递归，这样的复杂度是$O(n\log^2 n)$的

那么有覆盖时应该怎么做呢？

维护区间内所有数是否相等。

如果相等就可以直接打一个区间覆盖标记，直接 $ return$就好了

例题14

给定$n$个区间，以及每个点的价值$val[1…M]$，对于每个区间可以选择里面的一个点$i$，获得价值$val[i]$，每个点最多只能被选一次，求最大价值

$n,M\le5000$

明显是一个匹配问题，左边是含义为区间的$n$个点，右边是$m$个点，如果一个点在某个区间内，就从这个区间向这个点连边，然后用网络流——最大费用最大流去做，点数是$O(n+m)$，边数是$O(nm)$的，很明显，单单这么做是过不了的。

建一棵$1\sim m$的线段树，用线段树优化连边。

每个点都往自己的儿子连边，叶子节点就是代表右边的$m$个点，什么意思呢？

意思就是如果一个题目中所说的区间可以连接到线段树上的某个区间，那么他就可以连接这个线段树的区间内所有的叶子节点。

如果有一个区间$[L,R]$，就可以分成线段树上的$\log$个区间，之后连边到线段树区间就好了

点数$O(n+m)$，边数$O(n\log n)$

他说应该能过

例题15

有$n$个点，需要支持两种操作：

添加一条边，保证加完后还是森林

给定$(u,v)$，保证$(u,v)$是一条存在的边，求有多少点对$(x,y)$经过了了边$(u,v)$

可以离线

可以把树（森林）建出来，这时候我们的$(u,v)$肯定出在某一个包含它的连通块中，那么我们要求的就是这一条边一边的点数乘上另一边的点数，用并查集是可以很容易知道一个连通块有几个点的，所以只要求这条边在连通块中一边的点数，就可以知道另一边的点数

现在要求的问题是：求对于建完的这棵树，$v$的子树里有几个点现在跟$(u,v)$在一个连通块中

子树这个问题可以用$dfs$序解决，然后把一段连续的$dfs$序变成区间，比如说$v$子树的区间就是$[L(v),R(v)]$，那么问题就是求在$[L(v),R(v)]$种有多少个节点和$(u,v)$在一个连通块中。

用并查集维护连通块，用线段树记一下有几个点（下标就是$dfs$序的下标），合并集合时直接进行线段树合并，在询问的时候进行区间询问。

总复杂度$O(n\log n)$

原题链接：P4219 [BJOI2014]大融合

例题16

给定一个数组$a[1…n]$，首先有$Q$次操作，每次会将一个区间升序排序或者降序排序
求操作后$a[K]$的值

二分$a[k]$，大于$a[k]$标成$1$，小于$a[k]$标成0

然后线段树分裂(不会)

例题17被吃了

posted @ 2020-08-10 15:55 Loceaner 阅读(274) 评论(8) 编辑收藏举报

刷新页面返回顶部

Forever Young

Loceaner's Blog