「笔记」DP没入门就入土
写在前面
记录刷的DP题 以及 打死都不可能想到状态设计DP系列 汇总
线性DP
经典例题
LIS问题
即最长上升子序列问题。给定一个长度为 \(n\) 的数列 \(A\),求数值单调递增的子序列的最长长度是多少。
| 问题名称 | 最长上升子序列 |
|---|---|
| 状态表示 | \(f_i\) 表示以 \(A_i\) 为结尾的“最长上升子序列”的长度。 |
| 阶段划分 | 子序列的结尾位置(数列 \(A\) 的位置,从前到后) |
| 转移方程 | \(f_{i}=\max\limits_{0\le{j}\le{i},A_j<A_i}(f_j+1)\) |
| 边界 | \(f_0=0\) |
| 目标 | \(\max\limits_{i=1}^{n}f_i\) |
LCS问题
即最长公共子序列问题。给定两个长度分别为 \(n\) 和 \(m\) 的数列 \(A\) 和 \(B\)。求两数列的最长公共子序列长度。
| 问题名称 | 最长公共子序列 |
|---|---|
| 状态表示 | \(f_{i,j}\) 表示前缀子串 \(A_{1\sim i}\) 与 \(B_{1\sim j}\) 的最长公共子序列长度。 |
| 阶段划分 | 已经处理的前缀长度(两个数列中的位置,即一个二维坐标) |
| 转移方程 | \(f_{i,j}=\max\begin{cases}f_{i-1,j}\\{f_{i,j-1}}\\f_{i-1,j-1}+1(\text{if }A_{i}=B_{j})\end{cases}\) |
| 边界 | \(f_{i,0}=f_{0,j}=0\) |
| 目标 | \(f_{n,m}\) |
数字三角形问题
给定一个共有 \(n\) 行的三角矩阵,从上到下的第 \(i\) 行有 \(i\) 列。现在从矩阵的左上角出发,每次可以向下方或者向右下方走一步,并获得该位置的数,加入到当前数的总和中,最终到达三角矩阵的底层。求到达底层能获得的最大和。
| 问题名称 | 数字三角形 |
|---|---|
| 状态表示 | \(f_{i,j}\) 从左上角走到第 \(i\) 行第 \(j\) 列所得到的最大的和是多少。 |
| 阶段划分 | 路径的结尾位置(即矩阵中的行和列,一个二维坐标) |
| 转移方程 | \(f_{i,j}=\max\begin{cases}f_{i-1,j}\\{f_{i-1,j-1}}\end{cases}+a_{i,j}\) |
| 边界 | \(f_{1,1}=a_{1,1}\) |
| 目标 | \(\max\limits_{i=1}^n({f_{n,i}})\) |
容易发现,不管表示的状态是一维还是多维,DP算法在这些问题上都体现为作用在线性空间上的递推——DP的阶段沿着各个维度线性增长,从一个或多个边界点开始有方向地向整个状态空间转移、扩展,最终每个状态上都保留了以自身为目标的最优解。
AcWing271 杨老师的照相排列
题目分析
因为在合法方案中,每行每列的身高都是单调的,所以我们可以从高到低依次考虑标记为 \(1,2,\dots, n\) 的学生站的位置,发现 \(k\) 很小,所以可以考虑直接对每一排开一维数组,也就是开一个五维数组。当安排一名新的学生时,只需满足 \(a_i<N_i\) 且 \(i=1\) 或 \(a_{i-1}>a_i\) 即可。
状态
用 \(f_{a_1,a_2,a_3,a_4,a_5}\) 表示各排从左端起点分别站了 \(a_1,a_2,a_3,a_4,a_5\) 个人时,合影方案数量,\(k<5\) 的排用 \(0\) 替代即可。
边界
\(f_{0,0,0,0,0}=1\)。
转移
若 \(a_1< N_1\),那么令 \(f_{a_1+1,a_2,a_3,a_4,a_5}+=f_{a_1,a_2,a_3,a_4,a_5}\)。
若 \(a_2<N_2\),那么令 \(f_{a_1,a_2+1,a_3,a_4,a_5}+=f_{a_1,a_2,a_3,a_4,a_5}\)。
第 \(3\sim5\) 排同理。
目标
\(f_{N_1,N_2,N_3,N_4,N_5}\)。
代码见 DP笔记
AcWing272 LCIS 最长公共上升子序列
题目分析
此题为 LCS 和 LIS 的综合。但是不同的是公共的概念并不同,这点需要注意。将两算法结合,容易想到以下解法:
| 问题名称 | 最长公共上升子序列 |
|---|---|
| 状态表示 | \(f_{i,j}\) 表示 \(A_{1\sim{i}}\)、\(B_{1\sim{j}}\) 可以构成的以 \(B_j\) 为结尾的最长公共上升子序列的长度。 |
| 阶段划分 | 已经处理的前缀长度(两个数列中的位置,即一个二维坐标)。 |
| 转移方程 | \(f_{i,j}=\begin{cases}f_{i-1,j}&A_i\ne{B_j}\\\max\limits_{0\le{k}<j,B_{k}<{A_i}}(f_{i-1,k})+1&{A_i=B_j}\end{cases}\) |
| 边界 | \(f_{0,0}=0\) |
| 目标 | \(\max\limits_{j=1}^m\{f_{n,j}\}\) |
显然以上状态转移可以用三重循环的方式计算。但是这样肯定是过不了这道题的,时间复杂度的 \(O(n^3)\) 无法过掉 \(n,m\le3000\)。
因此考虑优化:在转移过程中,我们把满足 \(0\le{k}<{j},{B_k}<{A_i}\) 的 \(k\) 构成的集合称为 \(f_{i,j}\) 进行状态转移时的决策集合,记为 \(S(i,j)\)。注意到第二层循环时当 \(j\) 从 \(1\) 增加到 \(m\) 时,第一层循环 \(i\) 是一个定值,这使得 \(B_k<A_i\) 是固定的。因此当变量 \(j\) 加 \(1\) 时,\(k\) 的取值范围由 \(0\le{k}<{j}\) 变为 \(0\le{k}<{j+1}\),即整数 \(j\) 可能会进入新的决策集合,所以我们只需要 \(O(1)\) 检查 \(B_j\le{A_i}\) 是否满足,若满足则尝试更新当前取值。
所以上述式子只要 \(O(n^2)\) 时间内就可以解决,最终的目标即为 \(\max\limits_{j=1}^m\{f_n,j\}\)。
ps:AcWing 上的这道题 \(n=m\)。
代码见 DP笔记
此题转移部分的优化告诉我们,在实现状态转移方程时,要注意观察决策集合的范围随着状态的变化情况。对于“决策集合中的元素只增多不减少”的情景,就可以像此题一样维护一个变量来记录决策集合的当前信息,避免重复扫描,把转移的复杂度降低一个量级。
AcWing273 分级
题目分析
一个性质:一定存在一组最优解 \(B\),使得每一个 \(B_i\) 都在 \(A\) 数组中出现过。
证明:
此处以单调不降为例。
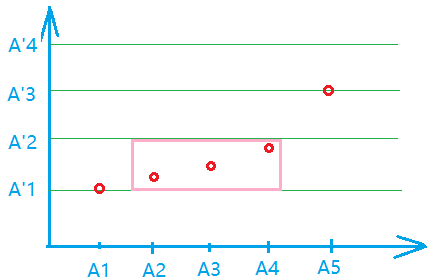
假设某个解如下图所示,其中 \(A\) 是原序列, \(A'\) 是将原序列排序后的序列,红圆圈表示每个 \(B_i\)。
考虑位于 \(A'_i,A'_{i+1}\) 之间的一段 \(B_i\),如上图中粉色框框出的部分。
则在 \(A\) 中粉色框对应的这一段中统计出大于等于 \(A'_{i+1}\) 的数的数量 \(x\),小于 \(A_i\) 的数的数量 \(y\),那么:
- 如果 \(x>y\) 则可以令粉色框中的 \(B_i\) 整体上移直到其中一个 \(B_i\) 碰到上边界使答案更优。
- 如果 \(x<y\) 则可以令粉色框中的 \(B_i\) 整体下移直到其中一个 \(B_i\) 碰到下边界使答案更优。
- 如果 \(x=y\) 则上述两种方式均可。
所以只要存在某个 \(B_i\) 的值不在原序列中,就可以将其挪到与原数列中某个数相同的位置,且答案不会变差。
用 \(f_{i,j}\) 表示已经排好了 \(B_{1\sim{i}}\) 且 \(B_i=A'_j\) 的最小花费。
依据倒数第二个数分配的是哪一个 \(A'_i\) 将 \(f_{i,j}\) 所代表的集合划分成 \(j\) 个不重不漏的子集。
代码见 DP笔记
AcWing274 移动服务
思路
容易发现DP的“阶段”就是“已经完成的请求数量”,通过指派一名服务员,可以从完成 \(i-1\) 个请求转移到完成 \(i\) 个请求。
不妨记录三个服务员的位置,将三个服务员的位置也放到DP的“状态”中,设 \(f_{i,x,y,z}\) 表示:完成了 \(i\) 个请求,三个服务员分别位于 \(x,y,z\) 时的最小花费。
那么容易想到转移方程有:
f[i][p[i+1]][y][z]=min(f[i][p[i+1]][y][z],f[i][x][y][z]+c[x][p[i+1]])f[i][x][p[i+1]][z]=min(f[i][x][p[i+1]][z],f[i][x][y][z]+c[y][p[i+1]])f[i][x][y][p[i+1]]=min(f[i][x][y][p[i+1]],f[i][x][y][z]+c[z][p[i+1]])
注意要特判每个位置不能相同,意义也比较明确,所以就不多说了。
但是这个算法的规模巨大,在 \(1000\times200^3\) 这个量级,肯定是不能承受的。但是我们发现当前一定有一个位置位于 \(p_i\),所以只需要知道阶段 \(i\) 和另外两名员工的位置即可描述一个状态,因此可以直接用 \(f_{i,x,y}\) 表示完成了前 \(i\) 个请求,其中一个员工位于 \(p_i\),其他两个员工分别位于 \(x\) 和 \(y\) 时的最小花费。之后的三种转移分别是让位于 \(p_{i},x,y\) 之一的员工前往 \(p_{i+1}\) 处理请求。
设 \(p_{0}=3\),则可以初始化 \(f_{0,1,2}=0\),最后的答案就是 \(\min\limits_{1\le{i},{j}\le{L}}f_{n,i,j}\)
代码见 DP笔记
启发
- 求解线性DP问题,一般先确定阶段。若阶段不足以表示一个状态,可以把所需的附加信息也作为状态的维度。
- 若转移时总是从一个阶段转移到下一个阶段,则没有必要关心附加信息维度的大小变化情况,因为无后效性已经由“阶段”保证。
- 在确定DP状态时,要选择最小的能够覆盖整个状态空间的“维度集合”。若DP状态由多个维度构成,则可以思考一下能否由几个维度推出另一个维度,从而降低空间复杂度。
AcWing275 传纸条
把路径长度作为DP的“阶段”,同时还要确定两条路径当前的末尾位置。设路径长度为 \(i\),第一条路径末尾位置位于 \(({x_1},{y_1})\),第二条路径末尾位置位于 \(({x_2},{y_2})\)。根据上一道例题的启发,我们要思考一下能否由几个维度推出另一些维度。
\(f_{k, i, j}\) 表示两个人同时走了 \(k\) 步,第一个人在 \((i, k - i)\) 处,第二个人在 \((j, k - j)\) 处的所有走法的最大分值。
转移:按照最后一步两个人的走法分成四种情况进行转移。
代码见 DP笔记
AcWing277 饼干
题目分析
比较巧妙的转化,但是输出方案的时候出了问题,迫使我看了y总的输出方案代码……不知道自己的为啥不行,放坑了
首先一个性质:贪婪度越大的孩子获得的饼干数应该越多。证明也不难证,直接用贪心中的临项交换法就行了,不再赘述。因此我们可以把小朋友按照贪婪值从大到小排序,这样之后他们分配到的饼干数量是单调递减的。
状态设计:设 \(f_{i,j}\) 表示前 \(i\) 个小朋友分了 \(j\) 块饼干所得到的最小怨气值总和。
状态转移:
- 如果第 \(i\) 个小朋友获得的饼干数不为 \(1\) 且 \(j>=i\),那么 \(f_{i,j}\) 的一个可行选择为 \(f_{i,j-i}\),这两个式子是等价的,前 \(i\) 个小朋友分了 \(j\) 块饼干等价于前 \(i\) 个小朋友分了 \(j-i\) 块饼干,原因是这样相当于每个人少拿一块饼干,但是获得的饼干数量的相对顺序是不变的,所以怨气值之和也是不会变的。
- 如果第 \(i\) 个小朋友获得的饼干数为 \(1\),那么就可以枚举前面有多少个小朋友获得的饼干数为 \(1\),从中取最小值,这一步可以用前缀和优化。
由此可得整个DP的转移方程为:
初始条件为 \(f_{0,0}=0\),最终目标为 \(f_{n,m}\)。
输出方案有点迷……
代码见AcWing277 饼干
洛谷 P3558 [POI2013]BAJ-Bytecomputer
思路
挺神的一道线性 \(\text{DP}\) 题。
发现最后的序列也是 \(-1,0,1\) 序列,因为改为别的值花费一定会变得更多。
设 \(f_{i,j}\) 表示前 \(i\) 个数字已经排好,第 \(i\) 个数字变为 \(j\) 的方案数,但是显然不能用负数下标,所以定义可以有一些修改。设 \(f_{i,j}\) 表示前 \(i\) 个数字已经排好,第 \(i\) 个数字变为 \(j-1\) 的方案数,那么能够用的数就是 \(f_{i,0},f_{i,1},f_{i,2}\),分别表示当前数为 \(-1,0,1\) 时的情况。
初始化整个 \(f\) 数组为 \(inf\),并且初始化 \(f_{1,a_1+1}=0\),因为第一个数为 \(a_1\) 的方案数显然为 \(0\)。
然后分情况讨论:
-
当 \(a_i=-1\) 时:
- 变为 \(-1\) 的方案数:因为当前数已经是 \(-1\) 了,所以 \(f_{i,0}=f_{i-1,0}\)。
- 变为 \(0\) 的方案数:如果要让 \(-1\) 变成 \(0\),前一个数必须是 \(1\),如果要 \(a_{i-1}\) 转化为 \(1\),那么当前数也必须是 \(1\),这样的话当前数就不能为 \(0\) 了,也就是说不能有 \(f_{i,1}\) 了,所以\(f_{i,1}=inf\)。
- 变为 \(1\) 的方案数:同上,如果要让 \(-1\) 变成 \(1\),前一个数必须是 \(1\),转移次数为 \(2\),所以此时的方案数为 \(f_{i,2}=f_{i-1,2}+2\)。
-
当 \(a_i=0\) 时:
- 变为 \(-1\) 的方案数:只能从上一个数变为 \(-1\) 的方案转移过来,转移次数为 \(1\),即 \(f_{i,0}=f_{i-1,0}+1\)。
- 变为 \(0\) 的方案数:当前数已经为 \(0\) 了,上一个数是 \(-1,0\) 都行,所以取上一个数两个方案数中的最小值即可,即 \(f_{i,1}=\min(f_{i-1,0},f_{i-1,1})\)。
- 变为 \(1\) 的方案数:同 \(a_i=-1\) 时的情况,之不管转移次数变成了 \(1\), 如果要让 \(0\) 变成 \(1\),那么前一个数需要是 \(1\),所以 \(f_{i,2}=f_{i-1,2}+1\)。
-
当 \(a_i=1\) 时:
- 变为 \(-1\) 的方案数:只能从上一个数变为 \(-1\) 的方案转移过来,转移次数为 \(2\),即 \(f_{i,0}=f_{i-1,0}+2\)。
- 变为 \(0\) 的方案数:前一个数必须是 \(-1\) 才能变成 \(0\),所以 \(f_{i,1}=f_{i-1,0}+1\)。
- 变为 \(1\) 的方案数:当前数已经为 \(1\) 了,上一个数是什么都行,所以直接取上一个数三个方案数中的最小值即可,即 \(f_{i,2}=\min(f_{i-1,0},f_{i-1,1},f_{i-1,2})\)。
综上转移方程汇总:
最后的答案显然就是 \(f_{n,0},f_{n,1},f_{n,2}\) 中的最小值。
注意要判断无解情况。
时间复杂度 \(O(n)\)。
代码见洛谷 P3558 [POI2013]BAJ-Bytecomputer
洛谷 P2679 子串
思路
这个题主要的难度在 \(DP\) 的状态设计上,如果 \(DP\) 状态设计好了,转移也就不难想了。
用 \(f[i][j][k][0/1]\) 表示A串中前 \(i\) 个字符,用了 \(k\) 个子串,匹配了B串前 \(j\) 个字符,用没用当前第 \(i\) 个字符的方案数,那么有
考虑初始条件
- 如果 \(A[i]=B[1]\),那么有 \(f[i][1][1][1]=1\)。
- b不难发现,\(f[i][1][1][0]\) 的值为 \(\sum\limits_{j=1}^{i-1}[A[j]=B[1]]\),表示不选第 \(i\) 个字符,从前 \(i\) 个字符中取出 \(1\) 个子串匹配B串第 \(1\) 个字符的方案数为 \(A[1\sim i-1]\) 中与 \(B[1]\) 相同的字符的个数。
最后的答案就是 \(f[n][m][k][0]+f[n][m][k][1]\)
至此 \(DP\) 就很明了了,但是空间是开不下的,但是发现 \(i\) 的转移只与 \(i-1\) 有关,所以可以用滚动数组去掉一维,这样就能过了。
时间复杂度为 \(O(nmk)\)。
代码见洛谷 P2679 子串
树形DP
AcWing285 没有上司的舞会
树形DP,找到一个不依赖别人的点作为根,然后进行树形DP,设 \(f_{i,1/0}\) 表示以 \(i\) 为根的子树,第 \(i\) 个点选或不选所能获得的最大价值,那么有:
最后取 \(\max(f_{R,0},f_{R,1})\) 就是答案,\(R\) 是选出的根节点,\(Son(x)\) 是 \(x\) 的子节点的集合。
代码见「考前日志」11.14
洛谷 P2014 [CTSC1997]选课
类似树上的分组背包问题。
设 \(f_{x,t}\) 表示在以 \(x\) 为根的子树中选 \(t\) 门课可以获得的最高学分,设 \(x\) 的子节点集合为 \(son_x\),子节点个数为 \(tot\)。修完 \(x\) 这门课之后,对于 \(x\) 的子节点 \(to\),可以在以 \(to\) 为根的子树中选修若干门课 \(c_{to}\),满足 \(\sum{c_{to}=t-1}\) 的基础上获得尽可能多的学分。
当 \(t=0\) 时,\(f_{x,t}=0\)。
当 \(t >0\) 时,有
代码见洛谷
AcWing287 积蓄程度
换根DP,树形DP
挺基础的换根DP了。随便找一个点作为根,记录每个点的度数,设 \(f_x\) 表示以 \(x\) 为根的子树,把 \(x\) 作为源点,从 \(x\) 出发流向子树的最大流量是多少,用 \(du_x\) 表示 \(x\) 的度数,有转移方程:
之后考虑换根求出以每个点为根的答案,设 \(g_x\) 表示以 \(x\) 为整棵树的根所能流过的最大流量,因为每个 \(x\) 的儿子 \(to\) 都已经处理完了自身子树内的最大流量 \(f_{to}\),所以只需要处理 \(x\) 除了以 \(to\) 为根的子树之外的部分对 \(g_{to}\) 的贡献,那么有:
发现是要自顶向下更新的,所以先更新,再进一步遍历。
调了挺久发现是数组开小了= =

代码见「考前日志」11.16
洛谷 P2018 消息传递
题目分析
贪心+树形DP
本来还以为要大费周折地换根,然后发现 \(n\) 很小,可以直接 \(O(n^2\log n)\) 枚举。
枚举每个节点作为根,用 \(f_x\) 表示走完以 \(x\) 为根的子树花费的最小时间。
那么如何更新呢?这个时候就要用到贪心的思想了。假设我们现在已经知道了 \(x\) 的儿子个数 \(tot\) 以及所有儿子 \(to\) 的 \(f\) 值。那么 \(x\) 必定要把信息传给每一个儿子,所以要尽量早地把信息传给 \(f\) 值较大的儿子,因此要把所有儿子的 \(f\) 值从小到大排序,并得出如下 DP 方程:
最后的答案需要加 \(1\),因为最开始要花费 \(1\) 的时间把消息传播到根节点。
计算出以每个点为根的答案之后取最小值,再扫描一遍找可以作为根的点即可。
特别注意
在更新当前节点时,需要记录所有儿子的 \(f\) 值,如果要定义临时数组只能在函数内定义,因为在接下来的 dfs 过程中又用到了此数组,数组中的值会因此发生改变,所以不能在外面定义。
洛谷 P6082 [JSOI2015]salesman
树形\(\texttt{DP}\) + 优先队列
比较容易看出来这是一道树形\(\texttt{DP}\)题
要注意的是最大停留次数为输入次数-1,因为还要从子树返回到这一个节点
然后下面考虑怎么\(\texttt{DP}\)
我们用\(f[i]\)表示以从\(i\)出发,访问以\(i\)为根的子树,并且最后能回到\(i\)的最大收益
显然我们要选较大且非负的数,因为去大点权的节点肯定比去小点权的点权更优,去非负点权的节点肯定比去负点权的节点更优,而且因为一个节点可以去多次且只记一次点权,所以肯定能够用完次数,因此我们每次在小于等于停留次数的前提下取完正儿子即可,这样就可以保证最大,所以\(f[i]\)就等于\(i\)所有正儿子的点权之和(前提是小于等于最大停留次数),最后的答案就是\(f[1]\)
下面来考虑解是否唯一的问题,解不唯一有两种情况:
- \(i\)的子树中有权值为\(0\)的点。因为选不选权值都不变,所以可选可不选,因此解就不唯一了
- 如果\(i\)在遍历过程中当父亲节点剩余的停留次数为\(1\)时,可选的最大值有两个及两个以上儿子节点,则解不唯一
所以在过程中判断一下就好了
代码见洛谷 P6082 [JSOI2015]salesman
状压DP
AcWing291 蒙德里安的梦想
状压DP
以行数以及此行的形态为状态。
设 \(f_{i,j}\) 表示前 \(i\) 行,第 \(i\) 行形态为 \(j\) 时的方案总数。此处 \(j\) 是一个用十进制整数记录的 \(m\) 位二进制数。 如果 \(j\) 二进制下当前位置为 \(1\),说明该位置为某个小长方形的上半部分,下一行的当前位置一定要放下半部分(即为 \(0\))。
如果为 \(0\) 表示其他情况,对下一行的形态无影响,但要保证连续的 \(0\) 的个数为偶数个。
对于当前行 \(i\) 的形态 \(j\),可以由上一行 \(i- 1\) 的形态 \(k\) 转移过来当且仅当:
- 当前行的形态 \(j\) 与上一行的形态 \(k\) 的与运算结果为 \(0\)。
这样保证了上一行形态中为 \(1\) 的位对应的当前位一定为 \(0\),满足上述条件。 - \(j\) 和 \(k\) 的按位或运算的二进制表示中连续 \(0\) 的个数为偶数个。
这样也就说明\(j\) 和 \(k\) 的二进制表示中连续 \(0\) 的个数为偶数个。
预处理合法(即连续 \(0\) 为偶数)的状态,然后 dp 即可。
代码见「考前日志」11.17
AcWing292 炮兵阵地
用 \(f_{i,j,k}\) 表示已经摆完前 \(i\) 行,且所有摆放的炮兵之间不能相互攻击到,每个炮兵都不在山地上,第 \(i\) 行的状态为 \(j\),第 \(i-1\) 行的状态为 \(k\) 的方案数。
因为第 \(i\) 行和第 \(i-1\) 行的状态已经确定了,但是当前阶段还和第 \(i-2\) 行的状态有关,所以要枚举第 \(i-2\) 行的状态,记为 \(u\)。
什么时候状态是合法的呢?
- \(j,k,u\) 三者表示的状态无交集。
- 第 \(i\) 行的炮兵没有摆放到山地上。
- 第 \(i\) 行的炮兵两两之间的距离\(\ge2\)。
显然满足上述条件的状态就是合法的。
转移: \(f_{i,j,k}=f_{i-1,j,u}+sum_i\)
其中 \(sum_i\) 表示第 \(i\) 行可以摆放的炮兵的个数。
代码见「考前日志」11.17
洛谷 P2831 愤怒的小鸟
未优化
状压\(\text{DP}\)
\(n\leq 18\),不是暴搜就是状压,因为我\(jio\)得状压会比较好理解,所以就写一篇状压的题解叭
首先我们要预处理出经过任意两点的抛物线可以击中的小猪有哪些,可以用\(line[i][j]\)来表示经过\(i,j\)的抛物线经过的小猪的集合,集合用二进制数来表示
-
这里有一个小问题就是如何求抛物线\(y=ax^2+bx\)中的\(a,b\)
假设目前的抛物线经过\((x_1,y_1)\)和\((x_2,y_2)\)两点,已知\(x>0\),那么有
\[y_1=ax_1^2+bx_1 \]\[y_2=ax_2^2+bx_2 \]则
\[ax_1+b=\frac{y_1}{x_1} \]\[ax_2+b=\frac{y_2}{x_2} \]两式做差得
\[a(x_1-x_2)=\frac{y_1}{x_1} - \frac{y_2}{x_2} \]所以
\(a=\frac{\frac{y_1}{x_1} - \frac{y_2}{x_2}}{(x_1-x_2)}\)
\(b=\frac{y_1}{x_1}-a*x_1\)
处理完之后就要想一想如何\(\text{DP}\)
我们设\(dp[s]\)表示消灭集合\(s\)内所有小猪所用的最少的小鸟数
显然\(dp[0]=0\),因为没有猪当然用不到鸟
假设当前的状态为\(s\),抛物线为经过\(i,j\)点的抛物线,这条抛物线打掉的小猪的状态为\(line[i][j]\),那么有
其中\(s|line[i][j]\)表示当前状态\(s\)在增加了经过\(i,j\)点的这条抛物线之后能打到的小猪的集合,显然要从\(dp[s|line[i][j]]\)和\(dp[s]+1\)中取最小
时间复杂度\(O(Tn^22^n)\)O(能过才怪),在洛谷上吸氧(\(O2\))可以过
优化
随意选择\(s\)内的一只小猪\(j\),那么\(j\)最后一定会被一只小鸟消灭,所以我们固定住这只小猪\(j\),只枚举\(k\)转移
更详细见AThousandSuns的题解
时间复杂度\(O(Tn2^n)\),稳了
51Nod 1683 最短路
题意
给定一个未知的\(0/1\)矩阵,对每个\(i\)求\((1,1)\sim(n,m)\)最短路为\(i\)的概率,在矩阵中不能向左走,路径长度为路径上权值为\(1\)的格子个数。
\(n\leq6,m\leq100。\)
思路
打死都不可能想到状态设计DP系列
参考了这篇博客的思路【51nod1683】最短路
概率乘了\(2^{n\times m}\)之后其实就是方案数,所以问题转化为了求满足题目条件的方案数
发现\(n\)很小,最大只有\(6\),考虑状压,但是不能直接维护当前格子的最短路,因为在多条并列最短路时会重复计数
考虑现在的\(0/1\)矩阵的特殊性:因为不能向左走,所以对于同一列中相邻两个格子之间的最短路最多相差\(1\)。因此考虑维护一整列最短路的差分数组。
记\(zt\)为一个三进制状态,表示该行从第二行开始,每个格子与上面的格子的差
设\(f[i][j][zt]\)表示第\(i\)列,第一行的最短路为\(j\),第\(2\)行~第\(n\)行的最短路的三进制为\(zt\)的方案数
转移时需要枚举下一列的\(0/1\)状态,线性更新一遍状态就可以了
时间复杂度为\(O(nm2^n3^{n-1})\)
矩阵优化DP
洛谷 P4910 帕秋莉的手环
题意
多组数据,给出一个环,要求不能有连续的\(1\),求出满足条件的方案数
\(1\le T \le 10, 1\le n \le 10^{18}\)
思路
20pts
暴力枚举(不会写
60pts
假设金珠子为\(0\),木珠子为\(1\),则不能有连续的木珠子
线性递推\(DP\),设\(f[i][0/1]\)表示当前填到第\(i\)位,第\(i\)位为金珠子/木珠子的方案数,那么有:
但是要分成两种情况讨论
-
第一个位置是\(0\),则\(f[1][0]=1,f[1][1]=0\),那么最后一个位置可以是\(0\)也可以是\(1\)
所以此时对答案的贡献为\(f[n][0]+f[n][1]\)
-
第一个位置是\(1\),则\(f[1][1]=1,f[1][0]=0\),那么最后一个位置只能是\(0\)
所以此时对答案的贡献为\(f[n][0]\)
时间复杂度\(O(Tn)\),期望得分\(60\)分
不知道为什么,也许是我写假了,只有48分
100pts
考虑用矩阵优化,目前的状态为\([f_{i,0},f_{i,1}]\),目标状态为\([f_{i+1,0},f_{i+1,1}]\),比较容易推出转移矩阵为
按照\(60\)分做法写矩阵快速幂就好了
区间DP
AcWing283 多边形
区间 DP,断环成链降低时间复杂度。
代码见「考前日志」11.14
AcWing284 金字塔
区间DP,用 \(f_{l,r}\) 表示子串 \(s_{l,r}\) 对应着多少种可能的金字塔结构。
为了防止重复,只考虑子串 \(s_{l,r}\) 的第一棵子树是由哪一段构成的,枚举第一棵子树的划分点 \(k\),令子串 \(s_{l+1,k-1}\) 作为第一棵子树,然后令子串 \(s_{k,r}\) 作为剩余部分。因为 \(k\) 不同,所以 \(s_{l+1,r-1}\) 就一定不同,因此就不会产生重复。
由此得到状态转移方程:
用记忆化搜索实现。
代码见「考前日志」11.14
51Nod 1327 棋盘游戏
以行为状态转移无法记录各列的状态,所以以列为状态转移
设\(f[i][j][k]\)为处理到第\(i\)列,前面有\(j\)列没有填棋子,有\(k\)行已经填到了右区间的方案数
记\(l[i],r[i],mid[i]\)分别为左区间右端点为\(i\)的行数、右区间左端点为\(i\)的行数、第\(i\)列没有被左右区间覆盖的行数
每次到达左区间右端点的限制\(l_{i}\)时,再考虑如何满足这些左区间,则有如下三种转移:
-
放在左区间内,就要满足将\(l_{i+1}\)行安排到前面没放棋子的\(j\)列中,因为顺序没有要求,所以直接乘上排列数,转移为
\[f[i+1][j+1-l_{i+1}][k+r_{i+1}]+=f[i][j][k]\times A_{j+1}^{l_{i+1}} \] -
放在右区间内,要乘上左右两侧的方案数
\[f[i+1][j-l_{i+1}][k+r_{i+1}-1]+=f[i][j][k]\times A_{j}^{l_{i+1}}\times (k+r_{i+1}) \] -
放在未被覆盖的中间位置,要乘上左侧和中间的方案数
\[f[i+1][j-l_{i+1}][k+r_{i+1}]+=f[i][j][k]\times mid_{i+1}\times A_{j}^{l_{i+1}} \]
初始状态为\(f[0][0][0]=1\),最后的答案为\(\sum_{i=1}^{m}f[m][i][0]\)
洛谷 P3592 [POI2015]MYJ
题意
给定\(m\)个区间\([a_i,b_i]\)以及\(c_i\),对于一个含有\(n\)个元素的序列\(ans[]\),区间\(i\)对其的贡献为\(\min\{ans_i\}(i\in[a_i,b_i])<=c_i\ ?\ \min\{ans_i\}(i\in[a_i,b_i])\ :\ 0\),要求构造一个序列\(ans[]\),最大化区间的贡献之和。
\(n\leq50,m\leq4000\)
思路
离散化+区间\(\texttt{DP}\)
稍作分析半天就会发现:存在一组答案使得每个\(ans_i\)都是某个\(c_i\)。因为把某个答案替换成第一个大于等于它的\(c_i\)不会更劣,因此\(c_i\)的值并不影响做题,但是大小顺序是有用的所以我们将\(c_i\)离散化。
因为一个区间的代价之和只与最小值有关,而且数据范围的\(n\)也不大,所以考虑区间\(\texttt{DP}\):
设\(f[l][r][k]\)表示区间\([l,r]\)内\(ans[]\)的最小值等于\(k\)的最大收益,\(g[p][j]\)为当前区间穿过\(p\),且\(c\geq j\)的区间数量
枚举最小的位置\(p\),那么包含\(p\)的区间的答案全都是\(k\),之后转移
\(\texttt{DP}\)时顺便记录记录决策点,然后\(dfs\)输出
时间复杂度\(O(n^3m)\)
最短路DP
洛谷 P4042 [AHOI2014/JSOI2014]骑士游戏
题意
有\(n\)个怪物,可以消耗\(k\)的代价消灭一个怪物或者消耗\(s\)的代价将它变成另外一个或多个新的怪物,求消灭怪物\(1\)的最小代价
思路
\(DP\)+最短路
看起来像是个\(\texttt{DP}\),认真思考一会儿也不难想到可以设计如下状态
设\(f[i]\)为消灭\(i\)所需的最小代价,那么有
其中\(to\)表示\(i\)点的后继
因为\(f\)的转移之间相互干涉,所以用最短路处理
先建双向边,方便之后转移,然后用\(\texttt{SPFA}\)(它死了求"多源"最短路就好了
因为不知道一开始应该打哪个怪物,所以干脆全都入队、全部更新就好了
\(ps:\)两年\(\text{OI}\)一场空,不开\(long\ long\)见祖宗
代码见洛谷 P4042 [AHOI2014/JSOI2014]骑士游戏
博弈论DP
洛谷 P5970 [POI2016]Nim z utrudnieniem
题意
\(\texttt{Nim}\)游戏,一共\(m\)颗石子分成了\(n\)堆,每堆石子数为\(a_i\),后手可以在游戏开始前扔掉\(d\)的倍数堆石子,但不能扔掉所有石子,求后手获胜方式有多少种。
\(d\leq10,n\leq5\times10^5,a_i\leq10^6\)\(m\)不直接给出但保证\(m\leq10^7\)
思路
\(\texttt{Nim}\)游戏后手必胜条件:每堆石子的个数异或和为\(0\)
设\(f[i][j][k]\)表示到第\(i\)个数,前\(i\)个数中选出的数的个数\(\text{mod}\ d=j\),异或和为\(k\)的方案数,每次枚举当前堆是否扔掉。
但是时间复杂度是\(O(nmd)\)的,显然不能过……
优化需要注意到异或具有的性质:任意个\(\leq x\)的数的异或和\(\leq2x\)。具体来讲就是说任意长度为\(k\)的数的异或和小于任意长度为\(k+1\)的数
因此可以考虑将所有堆的石子数从小到大排序,每次新加入一个数,数的上界一定不会大于\(2\times a_i\)
所以这样时间复杂度就变成了\(O(\sum\limits_{i=1}^na_id)=O(md)\)
但是空间超了,但是只有\(k\bigoplus a_i\)和\(k\)之间可以相互转移,所以可以开一个小空间\(t\),原地完成转移
还有就是\(n\)是\(d\)的倍数时会算上全选的情况,此时答案需要减\(1\)
常数很大,记得开\(O2\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号