「笔记」二分图

二分图学习笔记

定义

二分图又称二部图，是图论中的一种特殊模型，英文名叫 Bipartite graph。

二分图的节点由两个集合组成，且两个集合内部没有边。

百度的定义：

设\(G=(V,E)\)是一个无向图，如果顶点\(V\)可分割为两个互不相交的子集\((A,B)\)，并且图中的每条边\((i，j)\)所关联的两个顶点\(i\)和\(j\)分别属于这两个不同的顶点集\((i \epsilon A,j\epsilon B)\)，则称图\(G\)为一个二分图。

先来看一个比较正常的二分图

这个二分图还是很正常的，一看就知道左右两边的两个圈分别代表了上面所说的两个集合，两个集合内部的点都没有连边

再来看看下面几个二分图

二分图1

其实这个还算简单，并不难看出来是个二分图，转化一下子就变成了下面这个样子

再看一个：

二分图2

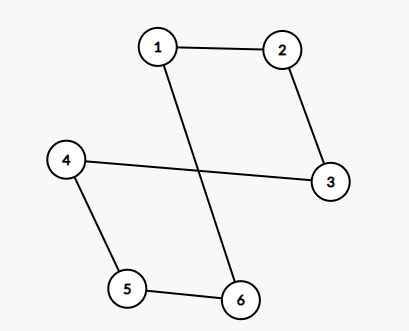
这个长得也不像二分图，然后你拖着拖着他就变成了下面这个样子，没错它也是个二分图

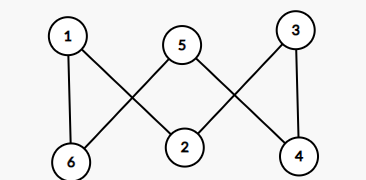
再看一个

二分图3

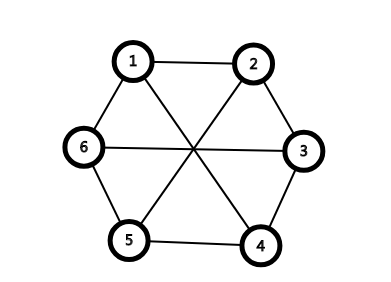
看到这个我的想法是：纳尼？这个是二分图！！

然而真香了，他的确是个二分图

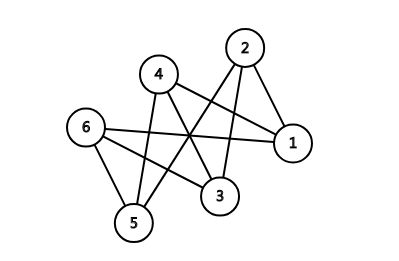
还有很多看起来十分鬼畜的二分图，我就不一一列举了。这上面的几个二分图告诉我们：不要相信你看到的东西

性质

1. 如果两个集合中的点分别染成黑色和白色，可以发现二分图中的每一条边都一定是连接一个黑色点和一个白色点。
2. 二分图不存在长度为奇数的环，如果一个图是二分图，那么它一定没有奇环，如果一个图没有奇环的话，那么它可以是二分图

因为每一条边都是从一个集合走到另一个集合，只有走偶数次才可能回到同一个集合

判定

染色法：假设\(\text{DFS}\)初始点\(A\)涂黑色，与它相邻的节点就涂白色。如果搜到某个点\(u\)的相邻点\(v\)已经涂色并且与\(u\)同色，就不可能是二分图了（找到了一个奇环）

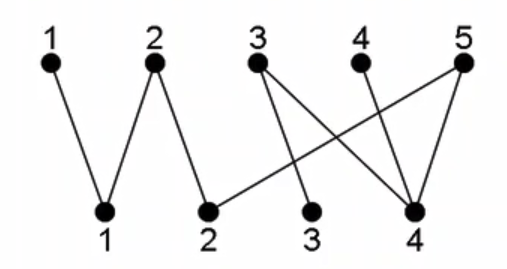
相关概念

匹配

给定一个二分图\(G\)，在\(G\)的一个子图\(M\)中，\(M\)的边集\(\{E\}\)中的任意两条边都不依附于同一个顶点，则称\(M\)是一个匹配

最大匹配

包含的边数最多的匹配

完美匹配

所有的点都在匹配边上的匹配

最佳匹配

如果\(G\)为加权二分图，则权值和最大的完美匹配称为最佳匹配

二分图最大匹配求法

1. 匈牙利算法 \(O(nm)\)
2. \(\text{HK}\)算法\(O(\sqrt{n}*m)\)
3. 网络最大流

二分图多重匹配求法

某些点可以被匹配多次

网络最大流

二分图最佳匹配求法

1. \(\text{KM}\)算法（优化版\(O(n^3)\)）
2. 网络最大流

匈牙利算法-求二分图最大匹配

交替路

从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。

增广路

从一个未匹配点出发，走交替路，如果途径另一个未匹配点 (出发的点不算），则这条交替路称为增广路（\(\text{agumenting path}\))

由增广路的定义可以推出下述三个结论

1. \(P\)的路径长度必定为奇数，第一条边和最后一条边都不属于\(M\)。
2. \(P\)经过取反操作可以得到一个更大的匹配\(M’\)。
3. \(M\)为\(G\)的最大匹配当且仅当不存在相对于\(M\)的增广路径。

算法轮廓：

1. 置\(M\)为空
2. 找出一条增广路径\(P\),通过取反操作获得更大的匹配\(M’\)代替\(M\)
3. 重复\(2\)操作直到找不出增广路径为止

时间复杂度：〇(nm)

/*
Author：loceaner
*/
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int A = 1e5 + 11;
const int B = 1e6 + 11;

inline int read() {
	char c = getchar(); int x = 0, f = 1;
	for( ; !isdigit(c); c = getchar()) if(c == '-') f = -1;
	for( ; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
	return x * f;
}

int n, m, match[A], E, vis[A], ans;
struct node { int to, nxt; } e[B];
int head[A], cnt;

inline void add(int from, int to) {
	e[++cnt].to = to;
	e[cnt].nxt = head[from];
	head[from] = cnt;
}

bool dfs(int now) {
	for(int i = head[now]; i; i = e[i].nxt) {
		int to = e[i].to;
		if(vis[to]) continue;
		vis[to] = 1;
		if(!match[to] || dfs(match[to])) {
			match[to] = now;
			return 1;
		}
	}
	return 0;
}

int main() {
	n = read(), m = read(), E = read();
	for(int i = 1, x, y; i <= E; i++) {
		x = read(), y = read();
		if(x > n || y > m) continue;
		add(x, y);
	}
	for(int i = 1; i <= n; i++) {
		memset(vis, 0, sizeof(vis));
		if(dfs(i)) ans++;
	}
	cout << ans << '\n';
	return 0;
}

其他相关概念

二分图最小顶点覆盖

是指最少的顶点数使得二分图\(G\)中的每条边都至少与其中一个点相连
二分图的最小顶点覆盖数=二分图的最大匹配数

有向无环图最小不相交路径覆盖

也称为最小边覆盖，是指用尽里少的顶点不相交的简单路径覆盖二分图中的所有顶点
路径长度可以为\(0\)
二分图的最小路径覆盖数=$ |V|$-二分图的最大匹配数

二分图最大独立集

最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。
对于一般图来说，最大独立集是一个\(NP\)完全问题，对于二分图来说最大独立集 =\(|V|\)-二分图的最大匹配数。