2019.10.12考试解题报告

总结

期望得分：\(100 + 40+ 0\)
实际得分：\(100 +40 + 0\)

没有挂分\(orz\)
在时间的安排上还是不合理，还是在\(T1\)上花了较长时间，不过幸好过了，做\(T2\)，只会暴力，\(T3\)~~日常神仙~~压轴题
数学不好，不会推式子
语文不好，读不懂题

思路

T1

题意：
给你一个满二叉树，有\(n+1\)层，它的根节点深度为\(0\)，其它节点的深度是它父亲节点的深度\(+1\)。求所有点对的最近公共祖先的深度和。

由于我太菜了，于是一开始手推了0、\(1、2\)的答案，~~发现我推不全~~，然后打了个树剖模板（我真是个智障），还去手动造数据……~~（我真是傻逼）~~

不过……结果是感人的，我推出了式子

T2

题意：
一张\(w*h\)的地图，每个格子都有一个建筑，每个建筑都有一个建筑重要度，现在要你投放一个炸弹，威力为\(p\)，向四周扩散，第\(i\)行第\(j\)列的格子的摧毁度为\(max(0, p - |x - i| - |y - i|)\)，每个格子受到的损失为建筑重要度和摧毁度的乘积，问最大损失和最小损失

我只会暴力，直接暴力枚举\(O(n^4)\)，完美\(40\)分~~

然而正解很懵逼

来自题解：

注意到我们没有必要对于每一个点暴力统计一遍答案。
当炸弹往右移动一格的时候，每个格子的摧毁度是这样变化的

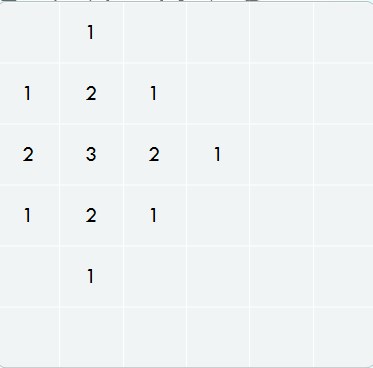
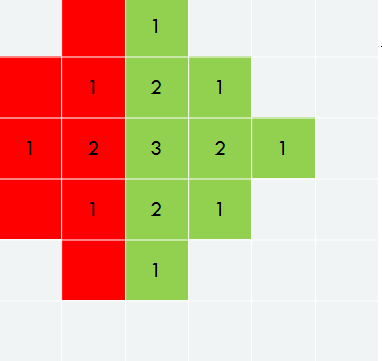
我们只需要维护红色部分与绿色部分的和，在往右移动一格的时候，由于红色部分与绿色部分只有边上会变化，那么总的改变个数为\(O(n)\)级别，于是我们就能\(O(n^2)\)枚举，\(O(n)\)维护，\(O(n^3)\)的时间复杂度解决了。
期望得分：\(100\)分

还可以更优吗？

事实上，我们只要记录对角线方向的前缀和就能做到 \(O(1)\) 维护，总复杂度 \(O(n^2)\)。

T3

沉迷于阅读理解无法自拔

代码

T1

考场代码

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
using namespace std;

inline int read() {
	char c = getchar();
	int x = 0, f = 1;
	for( ; !isdigit(c); c = getchar()) if(c == '-') f = -1;
	for( ; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + (c ^ 48);
	return x * f;
}

const int mod = 1000000007;

int n;

inline int power(int a, int b) {
	int res = 1;
	while(b) {
		if(b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

signed main() {
	freopen("commonants.in", "r", stdin);
	freopen("commonants.out", "w", stdout);
	n = read();
	cout << ((power(2, 2 * n + 2) % mod - (4 * n + 2) % mod * power(2, n)) % mod + mod - 2) % mod << '\n';
	return 0;
}

T2

暴力\(40\)

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define int long long
#define max(a, b) (a > b ? a : b) 
#define min(a, b) (a > b ? b : a)
using namespace std;

inline int read() {
	char c = getchar();
	int x = 0, f = 1;
	for( ; !isdigit(c); c = getchar()) if(c == '-') f = -1;
	for( ; isdigit(c); c = getchar()) x = (x << 3) + (x << 1) + (c ^ 48);
	return x * f;
}

const int N = 411;

int n, m, p, a[N][N], maxn = -1e5, minn = 1e17;

inline int solve(int x, int y) {
	int ax = x - p, ay = y - p, bx = x + p, by = y + p;
	if (ax <= 0) ax = 1;
	if (ay <= 0) ay = 1;
	if (bx > n) bx = n;
	if (by > m) by = m;
	int ans = 0;
	for(int i = ax; i <= bx; i++) {
		for(int j = ay; j <= by; j++) {
			ans += a[i][j] * max(0, p - (abs(x - i) + abs(y - j)));
		}
	}
	return ans;
}

signed main() {
	freopen("rts.in", "r", stdin);
	freopen("rts.out", "w", stdout);
	n = read(), m = read(), p = read();
	if(p == 1) {
		for(int i = 1; i <= n; i++)
			for(int j = 1, x; j <= m; j++)
				x = read(), maxn = max(maxn, x), minn = min(minn, x);
		cout << minn << " " << maxn << '\n';
		return 0;
	}
	for(int i = 1; i <= n; i++)
		for(int j = 1;j <= m; j++)
			a[i][j] = read();
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			int ans = solve(i, j);
			maxn = max(maxn, ans);
			minn = min(minn, ans);
		}
	}
	cout << minn << " " << maxn << '\n';
	return 0;
}

正解

#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
#include <map>
#include <complex>

#define lc k << 1
#define rc k << 1 | 1

#define inf 0x3f3f3f3f
 
using namespace std;
typedef long long ll;

int a[805][805];
int n, m, p;

ll mn = 1e13, mx = 0;

inline int dis(int x1, int y1, int x2, int y2){
	return min(abs(x2 - x1) + abs(y2 - y1), p);
}

void solve(int x){
	int y = 1;
	ll lres = 0, rres = 0;
	ll lsum = 0, rsum = 0;
	for(int i = x - p; i <= x + p; i ++){
		for(int j = y - p; j <= y; j ++){
			if(dis(i, j, x, y) != p) lsum += a[i + 200][j + 200]; lres += a[i + 200][j + 200] * (p - dis(i, j, x, y));
		}
	}
	for(int i = x - p; i <= x + p; i ++){
		for(int j = y + 1; j <= y + p; j ++){
			if(dis(i, j, x, y) != p) rsum += a[i + 200][j + 200]; rres += a[i + 200][j + 200] * (p - dis(i, j, x, y));
		}
	}
	//printf("%d %d %lld %lld %lld %lld\n", x, y, lres, rres, lsum, rsum);
	mn = min(lres + rres, mn);
	mx = max(mx, lres + rres);
	while(y < m){
		lres -= lsum;
		for(int i = y - p + 1; i <= y; i ++){
			lsum -= a[x + (p - 1 - y + i) + 200][i + 200];
			if(p - 1 - y + i != 0) lsum -= a[x - (p - 1 - y + i) + 200][i + 200];
		}
		y ++;
		for(int i = y; i <= y + p - 1; i ++){
			rsum += a[x + (p - 1 - i + y) + 200][i + 200];
			if(p - 1 - i + y != 0) rsum += a[x - (p - 1 - i + y) + 200][i + 200];
		}
		rres += rsum;
		for(int i = x - p + 1; i <= x + p - 1; i ++){
			rsum -= a[i + 200][y + 200]; rres -= a[i + 200][y + 200] * (p - dis(i, y, x, y));
			lsum += a[i + 200][y + 200]; lres += a[i + 200][y + 200] * (p - dis(i, y, x, y));
		}
	//	printf("%d %d %lld %lld %lld %lld\n", x, y, lres, rres, lsum, rsum);
		mn = min(lres + rres, mn);
		mx = max(mx, lres + rres);
	}
}

int main(){
	freopen("rts.in", "r", stdin);
	freopen("rts.out", "w", stdout);
	 
	scanf("%d%d%d", &n, &m, &p);
	memset(a, 0, sizeof(a));
	for(int i = 1; i <= n; i ++){
		for(int j = 1; j <= m; j ++){
			scanf("%d", &a[i + 200][j + 200]);
			//a[i + 200][j + 200] = 1;
		}
	}
	for(int i = 1; i <= n; i ++){
		solve(i);
	}
	printf("%lld %lld\n", mn, mx);
	return 0;
}

T3

~~考场代码没脸放~~

神奇的正解

#include <bits/stdc++.h>
 
using namespace std;
 
typedef long long ll;
const ll mod = 1e9 + 7;
ll C[1005][1005];
 
void pre(){
    C[0][0] = 1;
    for(int i = 1; i <= 1000; i ++){
        C[i][0] = 1;
        for(int j = 1; j <= i; j ++){
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
        }
    }
}
int n, m, c;
int a[105];
ll f[11][31][31];
ll g[11][31][31], h[11][31][31];
int main(){
	freopen("europe.in", "r", stdin);
	freopen("europe.out", "w", stdout);
	
    scanf("%d%d%d", &n, &m, &c);
    for(int i = 1; i <= c; i ++){
        scanf("%d", &a[i]);
    }   
    pre();
    for(int k = 1; k <= c; k ++){
        for(int i = 1; i <= n; i ++){
            for(int j = 1; j <= m; j ++){
                h[k][i][j] = C[i * j][a[k]];
                ll flag = -1;
                for(int jj = j - 1; jj >= 1; jj --){
                    h[k][i][j] = (h[k][i][j] + C[j][jj] * C[i * jj][a[k]] % mod * flag + mod) % mod;
                    flag = -flag;
                }
            }
        }
    }
    for(int k = 1; k <= c; k ++){
        for(int j = 1; j <= m; j ++){
            for(int i = 1; i <= n; i ++){
                g[k][i][j] = h[k][i][j];
            //  printf("%d %d %d %lld\n", k, i, j, g[k][i][j]);
                ll flag = -1;
                for(int ii = i - 1; ii >= 1; ii --){
                    g[k][i][j] = (g[k][i][j] + C[i][ii] * h[k][ii][j] % mod * flag + mod) % mod;
                    flag = -flag;
                }
            //  printf("%d %d %d %lld\n", k, i, j, g[k][i][j]);
            }
        }
    }
    f[0][0][0] = 1;
    for(int k = 1; k <= c; k ++){
        for(int i = 1; i <= n; i ++){
            for(int j = 1; j <= m; j ++){
                for(int ii = 0; ii <= i - 1; ii ++){
                    for(int jj = 0; jj <= j - 1; jj ++){
                        if((i - ii) * (j - jj) < a[k]) continue;
                        f[k][i][j] = (f[k][i][j] + C[i][i - ii] * C[j][j - jj] % mod * f[k - 1][ii][jj] % mod * g[k][i - ii][j - jj]) % mod;
                    }
                }
            }
        }
    }
    ll ans = 0;
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= m; j ++){
            ans = (ans + C[n][i] * C[m][j] % mod * f[c][i][j]) % mod;
        }
    }
    //printf("%d %d %d\n", n, m, c); 
    printf("%lld\n", ans);
    return 0;
}

posted @ 2019-10-12 15:38 Loceaner 阅读(139) 评论(8) 编辑收藏举报

刷新页面返回顶部

Forever Young

Loceaner's Blog

2019.10.12考试解题报告

2019.10.12考试解题报告

总结

思路

T1

T2

T3

代码

T1

T2

T3

公告