「笔记」浅谈逆序对

浅谈逆序对

$$传送门qwq$$

---

题目描述

猫猫\(TOM\)和小老鼠\(JERRY\)最近又较量上了，但是毕竟都是成年人，他们已经不喜欢再玩那种你追我赶的游戏，现在他们喜欢玩统计。

最近，\(TOM\)老猫查阅到一个人类称之为“逆序对”的东西，这东西是这样定义的：

对于给定的一段正整数序列，逆序对就是序列中\(a_i\)>\(a_j\)且\(i\)<\(j\)的有序对。

知道这概念后，他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。

Update:数据已加强。

---

输入输出格式

输入格式：

第一行，一个数\(n\)，表示序列中有\(n\)个数。

第二行\(n\)个数，表示给定的序列。序列中每个数字不超过\(10^9\)

输出格式：

给定序列中逆序对的数目。

---

本蒟蒻今天学习了树状数组，今天来更新啦

思路1

逆序对是什么东西呢，在题目已经给出介绍了

对于给定的一段正整数序列，逆序对就是序列中\(a_i\)>\(a_j\)且\(i\)<\(j\)的有序对。

比如你有一个\(a\)数组，如果在这个数组中中\(a[i]\)>\(a[j]\)并且\(i\)<\(j\)，我们就称它是一个逆序对

这个题就是要求我们求出输入的数中逆序对的数量

求逆序对的方法有很多种，可以用树状数组，也可以用线段树，但由于本蒟蒻没有学过这俩玩意儿，所以只会用归并排序，那么归并排序又是什么呢

归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列;即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

可以来这里理解一下什么是归并排序

那么归并排序有什么优点呢？

* 归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治策略
* 归并排序是稳定排序
* 归并排序的最好，最坏，平均时间复杂度均为O(\(nlogn\))。

如何实现求逆序对？？

假设我们手头有两个已经从小到大排好序的数组，且他们分别是原来的一段大数组的前半段和后半段，现在我们的比较到了X,Y位置

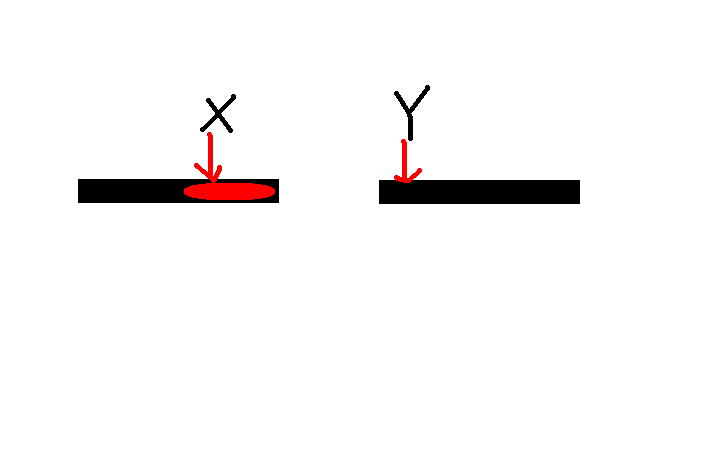
假使X>Y则其必然构成一对逆序对，与此同时我所画出的红色的这一段的的数均大于Y，所以逆序对的数量就要加上这一段的长度

而对整个数组都归并排序完毕后最终就可以得到逆序对的和

代码

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;

int n;
long long ans;
int a[5000007],b[5000007];

void sort(int l,int r) {
	if(l==r)return;
	int m=(l+r)>>1;
	sort(l,m);
	sort(m+1,r);
	int i=l,j=m+1,k=l;
	while(i<=m&&j<=r) {
		if(a[i]<=a[j])b[k++]=a[i++];
		else ans+=m-i+1,b[k++]=a[j++];
	}
	while(i<=m)b[k++]=a[i++];
	while(j<=r)b[k++]=a[j++];
	for(i=l; i<=r; ++i)a[i]=b[i];
}

inline int read() {
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		s=s*10+(ch-'0');
		ch=getchar();
	}
	return s*w;
}

int main() {
	scanf("%d",&n);
	for(int i=1; i<=n; i++) {
		a[i]=read();
	}
	sort(1,n);
	printf("%lld",ans);
	return 0;
}

思路2

我们可以用树状数组实现

离散化一下，直接将输入的数变为负数，在之后按价值从小到大排序，排完序之后再用树状数组维护，并每次把这个数的位置加入到树状数组中

因为是排完序之后，所以之前加入的一定比后加入的大，然后在查询当前这个数前面位置的数（是前面位置的数，要当前这个数减1），就是逆序对的个数了

代码

#include<bits/stdc++.h>
#define N 500110
#define lowbit(i)  i&-i
using namespace std;

int n,a[N],b[N],t[N];
long long ans=0;

inline int read(){
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar())if(c=='-')f=-1;
    for(;isdigit(c);c=getchar())x=x*10+c-48;
    return x*f;
}

inline void insert(int x){
    for(int i=x;i<=n;i+=lowbit(i)){
        t[i]++;
    }
}

inline int find(int x){
    int ans=0;
    for(int i=x;i;i-=lowbit(i)){
        ans+=t[i];
    }
    return ans;
}

int main(){
    n=read();
    for(int i=1;i<=n;i++)a[i]=b[i]=-read();
    sort(b+1,b+1+n);
    for(int i=1;i<=n;i++){
        a[i]=lower_bound(b+1,b+n+1,a[i])-b;
    }
    for(int i=1;i<=n;i++){
        ans+=find(a[i]-1);
        insert(a[i]);
    }
    cout<<ans<<'\n';
    return 0;
}