洛谷P1983 车站分级

题目链接

https://www.luogu.org/problemnew/show/P1983

---

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n的 n 个火车站。每个火车站都有一个级别，最低为 1级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2 级）却未停靠途经的 66号火车站（亦为 2 级）而不满足要求。

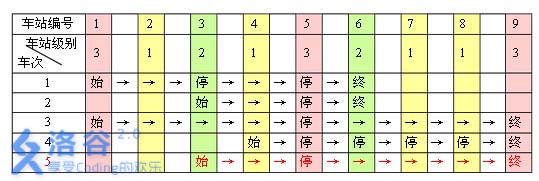
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

---

输入输出格式

输入格式：

第一行包含 2 个正整数 n, m，用一个空格隔开。
第 i + 1 行(1≤i≤m)中，首先是一个正整数s (2≤s≤n)，表示第 i 趟车次有 s 个停靠站；接下来有 s 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

一个正整数，即 nn 个火车站最少划分的级别数。

---

代码

#include<iostream>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<cstdio>
using namespace std;

const int maxn=1010;
int n,m;
int f[maxn];//flag标记
int top,first,ans=0;//ans答案
int vis[maxn],s,a[maxn],e[maxn][maxn];//邻接矩阵存储
int ru[maxn];//存入度的数组
int s_tack[maxn];//手打栈

//快读qaq
inline int read() {
	char c=getchar();
	int x=0,f=1;
	while(c<'0'||c>'9') {
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-48,c=getchar();
	}
	return x*f;
}

//输入、初始化和初步处理
void init() {
	n=read();
	m=read();
	for(int i=1; i<=m; i++) {
		memset(f,0,sizeof(f));
		s=read();
		for(int j=1; j<=s; j++) {
			a[j]=read();
			f[a[j]]=1;//已标记过
		}
		for(int j=a[1]; j<=a[s]; j++)
			if(!f[j]) //如果没有标记过，将其标记
				for(int k=1; k<=s; k++)
					if(!e[j][a[k]]) { //如果没有值
						e[j][a[k]]=1;//将其值定为1
						ru[a[k]]++;//a[k]这个点的入度加一
					}
	}
}

void topsort() { //拓扑排序
	first=1;
	while(top!=0 || first!=0) {
		first=0,top=0;
		for(int i=1; i<=n; i++) {
			if(!ru[i] && !vis[i]) {
				s_tack[++top]=i;
				//如果这个点的入度为零并且没有访问过就将其入栈并标记为访问过
				vis[i]=1;
				//标记已访问过
			}
		}
		for(int i=1; i<=top; i++) {
			for(int j=1; j<=n; j++) {
				if(e[s_tack[i]][j]!=0) {
					e[s_tack[i]][j]=0;
					ru[j]--;
				}
			}
		}
		ans++;
	}
	ans--;
	//因为当top为零的时候累加器还在累加，所以最后要减去1
	printf("%d",ans);//愉快输出
}

int main() {
	init();
	topsort();
	return 0;
}