语言及其文法

基本概念

字母表

• 字母表\(\Sigma\)：有穷符号集合

字母表上的运算

• 乘积

  \(\Sigma\)₁\(\Sigma\)₂ = { ab|a\(\in\)\(\Sigma\)₁, b\(\in\)\(\Sigma\)₂ }

• n次幂

  字母表的n次幂：长度为n的符号串构成的集合

  • \(\Sigma\)⁰ = { \(\varepsilon\) }
  • \(\Sigma\)ⁿ = \(\Sigma\)^n-1\(\Sigma\) , n$\geq$1

• 正闭包

  字母表的正闭包：长度正数的符号串构成的集合

  \(\Sigma\)⁺ = \(\Sigma\) U \(\Sigma\)² U \(\Sigma\)³ U ...

• 克林闭包

  字母表的克林闭包：任意符号串（长度可以为零）构成的集合

  \(\Sigma\)^* = \(\Sigma\)⁰ U \(\Sigma\)⁺ = \(\Sigma\)⁰ U \(\Sigma\) U \(\Sigma\)² U \(\Sigma\)³ U ...

串

• \(\forall\) x \(\in\) \(\Sigma\)^*，x称为\(\Sigma\)上的一个串
• 串是字母表中符号的一个有穷序列
• 串s的长度|s|：s中符号的个数
• 空串 \(\varepsilon\) ：长度为0的串

串上的运算

• 连接

  • 如果 x 和 y 是串，那么 x 和 y 的连接是把 y 附加到 x 后面而形成的串，记作 xy

  • 空串是连接运算的单位元，即对于任何串s 都有：\(\varepsilon\)s = s\(\varepsilon\) = s

  • 设x,y,z 是三个字符串，如果 x= yz则称 y 是 x 的前缀，z 是 x 的后缀

• 幂

  串s的n次幂：将n个s连接起来

  • s⁰ = \(\varepsilon\)
  • sⁿ = s^n-1s , n$\geq$1

文法定义

形式化定义

G = ( V_T , V_N , P , S )

• V_T：终结符集合

  终结符(token)：文法定义的基本符号

• V_N：非终结符集合

  非终结符(nonterminal)：表示语法成分的符号，又称语法变量

  V_T \(\cap\) V_N = \(\phi\)

  V_T \(\cup\) V_N ：文法符号集

• P：产生式集合

  产生式：描述终结符和非终结符组合成串的方法

  产生式一般形式：\(\alpha\) \(\rightarrow\) \(\beta\) \(\alpha\)定义为\(\beta\)

  产生式头部/左部：\(\alpha\) \(\in\) ( V_T  \(\cup\) V_N )⁺

  产生式体/右部：\(\beta\) \(\in\) ( V_T \(\cup\) V_N )^*

• S：开始符号

  开始符号表示该文法中最大的语法成分

  S \(\in\) V_N

符号约定

终结符

• 字母表中排在前面的小写字母

• 运算符

• 标点符号

• 数字

• 粗体字符串

非终结符

• 字母表中排在前面的大写字母
• 字母S：通常表示开始符号
• 小写、斜体的名字
• 代表程序构造的大写字母：E(表达式)、T(项)、F(因子)

文法符号

• 字母表中排在后面的大写字母（即终结符或非终结符）

终结符号串

• 字母表中排在后面的小写字母（包括空串）

文法符号串

• 小写希腊字母（包括空串）

开始符号

• 除非特别声明，第一个产生式的左部是开始符号

产生式简写

• 一组有相同左部的\(\alpha\)产生式：\(\alpha\)\(\rightarrow\)\(\beta\)₁, \(\alpha\)\(\rightarrow\)\(\beta\)₂, ... , \(\alpha\)\(\rightarrow\)\(\beta\)_n，可简记为：\(\alpha\)\(\rightarrow\)\(\beta\)₁|\(\beta\)₂|...|\(\beta\)_n

  \(\beta\)₁，\(\beta\)₂，\(\beta\)_n 称为\(\alpha\)的候选式

语言定义

推导和归约

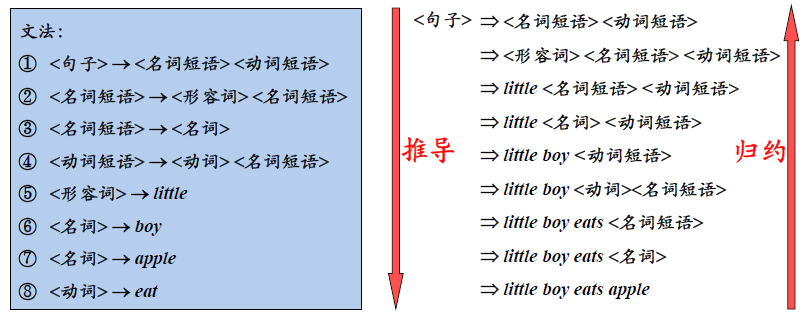
• 推导：用产生式的右部替换左部

  

• 归约：用产生式左部替换右部

句型和句子

语言的形式化定义

语言上的运算

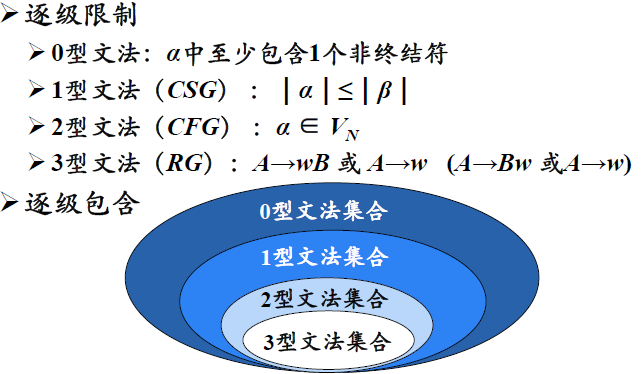
文法分类

0型文法(PSG)

产生式左边至少有一个非终结符

1型文法(CSG)

产生式右边比左边长

• 非终结符A上下文均为 \(\alpha\)₁ \(\alpha\)₂ 时，才可以替换为\(\beta\)

2型文法(CFG)

产生式左边只由非终结符

3型文法(RG)

产生式左边是一个非终结符，右边是0/1个非终结符和终结符号串

w：终结符号串

右边非终结符在左即左线性，在右即右线性

四种文法间的联系

CFG分析树

基本概念

图形化表示

分析树是推导的图形化表示

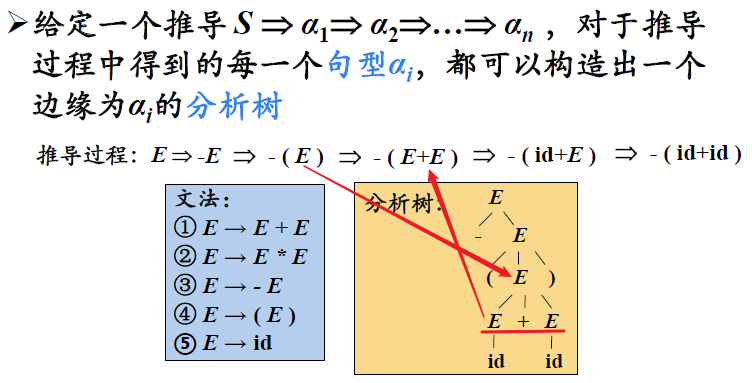
句型的短语

二义性文法

• 如果一个文法可以为某个句子生成多棵分析树，则该文法是二义性的
• 对于任意一个上下文无关文法，不存在一个算法，判定它是无二义性的；但能给出一组充分条件，满足这组充分条件的文法是无二义性的