总结
一、常见错误
代码细节
- 当两个特别大的数相乘后取模时,要使用快速乘。
- 注意:使用long long时,要检查传参是否传int。
- 注意:不要3数连乘 不要int×int 不要忘记负数 不要忘模 (long long范围)。
- 数组大小,乘2,乘4等问题。
- 数组类型,连续定义有时会错(如把int定义成bool)。
- 不要忘记初始化。
- 多测清空问题:每定义一个变量,数组,就要添加对应的清空代码。
- 除法,逆元可能被卡(虽然模数是质数,但除数模完后,可能是0)。要尽量避免求逆元。对于上述情况,可以定义一个结构体维护,额外记录下0的个数。
- 不能直接把字符串(char*)作为stl容器的类型,可以转换为string或手写比较函数,否则会错。
其它
-
2-SAT:a->b即!b->!a 两条边都要连。
-
splay,lct注意事项:
-
旋转时fa的连接。
-
旋转时新根的fa。
-
旋转时旧根的fa的儿子要赋值为新根。
-
维护标记:
旋转后,2次上传
splay前,下放标记
access更换重儿子时,上传
cut后,上传(也许)
-
-
行列式,高斯消元等的乘法值要预处理出来,否则会错,就是
int t=1ll*sz[j][i]*ksm(sz[i][i],md-2)%md; -
线段树合并,主席树的空间要略大于。
-
线段树合并要特判叶子节点。
-
a/b 向上取整 (a+b-1)/b 要特判负数。
-
注意输出-0.00的问题。
-
使用标记永久化,上传时要注意考虑标记。
-
主席树在新建节点时要把原来的复制全。
-
点在多边形内部判定,需要考虑点在边界上的情况。
-
在树dfs时,如果需要的临时变量是公用的,那么需要先进行所有子树的dfs,防止正在使用的这个变量被子树破坏(通常是树形背包)。
-
如果题目中要求无解输出-1,那么需要特判这种情况,以免会输出-inf。
-
读题时要认真仔细,把题目条件和要求看全。
-
&&和||是短路运算符,即前半部分满足要求就不会执行后半部分。而这有时可能会造成问题。
-
对于multiset,erase(x)会删除所有元素x。如果只想删去一个,可以使用erase(find(x)),用迭代器删除。
-
在程序调试或卡常时,尽量不要开O2优化。比如在使用除0进行断点调试时,O2可能无法收到浮点数例外。
-
注意自环重边。
-
用double尽量要注意值域问题,避免丢精。可以考虑一些代换以缩小值域。
-
double意义下的组合数用杨辉三角比阶乘精度高。
二、一些技巧
一、动态规划
DP设计
-
互质数的选择,当质因数较大时采用分组背包,较小时状压记录,以平方根为界(luogu寿司晚宴)。
-
对于状态转移有环的动态规划,使用如下方式求解:
-
若转移里没有max/min,只有加减乘除运算,可以建立方程组,通过高斯消元在O(n^3)得出解。
-
若转移只是对一些元素取max/min(或第k大/小值),再加/减一个值,可以建图,使用dij或spfa求解。
-
若u依赖v,且若v能更新u,则dp[u]>=dp[v],且求的是min(例如dp(u)=min(S(u)+∑dp[v],K(u)))。
每次:
1:把值最小的点标记
2:if 一个点u依赖的所有v都被标记
计算dp(u),并标记u,
3:回到1
直到所有点被标记。
就结束。 -
若2,3都不满足,可以使用如下方法:
先把每个点都入队,每次从队首取出u,并计算dp(u),若dp(u)发生更新,则把依赖u的v都加入队列(前提是v不在队列中)。
这个方法很像spfa,但时间复杂度最坏为O(nm)。
例题:模拟赛tiger,luogu 骑士游戏
-
-
每次找一段删除,删除后自动合并的DP的一种解决方法:
先设dp(i,j)表示考虑i~j的结果
然后,考虑i这个点的情况:i一定是和之后的几段一起合并后删除
例如:i j
-----*****--@@-&&&&&--------
而中间的几段一定不能一起删除因此,像
------####------#####-------这种情况是不可能的
所以,中间的段就是单独的子问题了。
还要加一组状态k,表示之前的连续段的信息。 -
对于树形背包,通常,我们有两种方法:
基于dfs合并,可以知道每个点的确切情况(比如子树中选了多少),但是,复杂度较高(因为合并背包很慢)。
在dfs序上DP,复杂度较低,但是,不能 知道每个点的确切情况(因为是在序列上)。 -
有字典序限制的DP(以大于为例):
通常,我们有两种方法:
1、记录下当前是“放什么都大于(之前已经大于)”,还是“放大于的才大于”。
这个通常用于数位dp
但是,这个会使数有本质区别,难以处理。
2、确定一个前缀一模一样,下一位大于,之后随意。
这样我们可以根据前缀算出当前状态,并且之后的dp不受影响。
但是,有时这样复杂度较高,并且,如果有多个有字典序限制,这个方法就不适用了。 -
若在树上进行类似“随机游走的”DP,可以不用高斯消元:
1、设=。
2、由于u的计算仅依赖u的父亲和儿子,把儿子用“1”的方法表示,儿子的父亲是本身,这样u就只依赖u和父亲。
3、通过移项,使u仅依赖父亲,进而表示为“1”中的形式。
4、最后,根节点的b就是答案。 -
有些容斥原理可以DP,在奇偶性改变时,取相反数即可。
-
关于连通图计数的DP,可以设表示个点连通的方案数,转移时先算出方案总数,再减去不连通的。不连通的可以枚举编号最小的点所在连通块的点数,用减去,其中是剩余的个点的方案总数。当图相对复杂(比如完全二分图)时,可以增加一维状态,同时也要多一层枚举。
-
树形的有依赖dp也可以分两次dp,分别考虑向上和向下传递(即换根dp)。
-
dp套dp:通过外层dp,算出使某个问题的解为给定值的方案数等,其中这个问题需要用内层dp解决。
按照内层dp所需要的输入顺序进行外层dp,将内层dp转移所需要的依赖(可以观察填表的过程)通过状压记录成状态(可以预处理出这些状态的转移自动机),进行dp。 -
数位DP可以统计L到R之间的之和。要求f只和x的数位有关。若f本身就是递推式,可以按照f的递推顺序进行数位DP,并设F表示在限制下f之和,并把f的转移式子改成F的。
-
数位DP若需要记录进位信息,可以从低位到高位进行dp。例题
-
有时,可以用两种方式表达计数DP,根据这两种表示法相等的,来列方程求解。
-
秩为x的矩阵计数可以DP,只要记录当前的秩,转移时考虑是否增加秩即可。
-
麻将题(横三竖三的),可以dp,因为三个横的就能变成三个竖的,因此横的不会超过2个,可以压进dp状态。具体细节
-
区间DP通常有两种转移形式:从两端删除,或从中间分裂。
-
涉及到矩形计数,最大矩形等问题时,可以考虑悬线法,配合单调栈,枚举一个数作为区间的最小值。
-
网格图中的放置可以考虑插头DP,就是记录当前考虑的行上面每一列的信息。
-
记录几个变量的相等关系,可以使用最小表示法。
-
类似双人猜数游戏的问题,可以使用DP:设f(i,...)表示答案为...,在第i步能否猜出。则f(i,...)=f(i-2,...),同时如果与...产生混淆xxx的都满足f(i-1,xxx)=1,且f(i-1,...)=0,则f(i,...)=1。
DP优化
-
对于有些DP,可以先设计出比较简单的状态后,去掉一些无用状态,等价状态,进行优化。(可以使用记忆化搜索)
-
带权二分:若选择dp等满足凸性,可以用直线切割凸包,将选的代价修改,通过二分找到合适的位置。
-
在对DP进行卡常优化时,可以试试改成记忆化搜索,有时能快很多。
-
如果转移时需要枚举相交的区间,可以使用容斥,转化为枚举不相交的区间,这样l和r就没有联系了,可以分开计算,从而减少一维。
-
对于一般的01背包,复杂度为,但如果物品体积的范围C不算大,可以按照C去依次计算,当考虑到体积为x的物品时,对于模x意义下相等的数,从小到大满足决策单调性,使用分治,可以把复杂度降低至。
void dfs(int l,int r,int l2,int r2,int x,int s) { if(l>r)return; int m=(l+r)>>1,wz=0; for(int y=l2;y<=r2&&y<=m;y++) { if(m-y>=su[x].size()) continue; ll t=dp[x*y+s]+su[x][m-y]; if(t>jh[x*m+s]) jh[x*m+s]=t,wz=y; } dfs(l,m-1,l2,wz,x,s);dfs(m+1,r,wz,r2,x,s); } for(int i=1;i<=300;i++) { for(int s=0;s<i;s++) { int t=(k-s)/i; dfs(0,t,0,t,i,s); } for(int x=1;x<=k;x++) { dp[x]=jh[x]; jh[x]=0; } } -
在dp转移时如果需要卷积,但是和他卷积的数组差分后容易维护(比如),可以不用NTT,直接用前缀和维护。
-
解决LIS问题,如果序列很长,但序列具有相似性,且值域不大,也可以设表示以x结尾,长度为y的LIS,然后按顺序枚举x,滚动数组进行更新。
-
对于递推,如果需要区间询问(比如询问区间内不同子序列数目),可以把转移写成矩阵,然后算出前缀积和逆矩阵的前缀积。注意乘法的顺序
-
每次把子节点的其中一维DP状态取最大/最小的DP可以使用线段树合并优化。(NOID1T2)
-
枚举子集可以使用复杂度为的做法,如果不需要使用所有子集的补集的信息(比如向所有子集连边),也可以每次去掉一个元素,复杂度。
-
计数DP如果转移时有多重循环,并且他们之间存在一定的不相关性,可以拆成多步进行DP,或者使用乘法分配律进行优化。这个技巧非常常见,但有时不容易发现(AT5620,USACO_PT_T2)。
-
对于一些树形DP,有可能满足是关于的分段函数。由于分段函数相加,求前后缀最值都不会改变总段数,因此可以证明段数和子树大小相关。用线段树合并或者可并堆维护折线可以优化算法。(APIO烟火,树上保序回归等等)
-
数位DP如果有多组询问,可以先在不考虑字典序的情况下设表示后n位数,前面的数位造成的影响为的答案。
询问时枚举lcp长度和第一个不同的数字并算出对应的,然后直接利用算好的数组更新答案即可。这样就不需要每次都DP
了。
-
计算方案数的背包问题中,如果要删除物品,可以使用多项式除法O(m)计算,没必要重来一遍。用这种思想来优化多组询问的背包很常见。(抽奖机,假面)
二、字符串
- AC自动机算法在匹配时,在fail树上的链将都被匹配,所以经常与树上算法联合使用(luogu P3796,luogu P2336喵星球上的点名)。
- 后缀自动机跳fail的注意事项 (压缩字符串)。
- 处理类似重复子串的问题,可以考虑枚举长度L,然后每隔L放一个关键点,并计算相邻的关键点的lcp,lcs等信息。
- 扩展后缀数组:在trie树上构建,使用倍增,类似普通SA。
- 处理回文的问题时,可以枚举回文中心。为了减少细节,有时可以在每个字符后面加入#等特殊字符。
- 回文自动机(PAM)
- 前后添加的哈希,可以从中间开始,维护左边的后缀,右面的前缀的(从左到右的)哈希值。询问子串时拼接即可。或者维护懒标记。
- 某定理:本原平方串为所有形如的串。其中不是整周期循环串。所有本原平方串的个数是的。本质不同的本原平方串的个数是的。详见循环串。
- Border:一个字符串的可以拆分为个等差数列,这个性质常常用于优化。回文的回文后缀就是border。
- 判断双回文串只要检查最长回文前后缀即可。
三、数学
数论等
-
快速乘代码:
ll ksc(ll a,ll b) { return (a*b-(ll)((long double)a/md*b)*md+md)%md; } -
中国剩余定理,可以在计算时之算出前缀积(变算边乘),复杂度可以从降到,在计算时调整下余数即可。如果需要高精维护,此法可以起到优化。
-
1到n中所有数的约数的约数个数和大概是的。
-
带变量x的组合数,可以把组合数拆开变成下降幂,用斯特林数+二项式定理表示出系数,从而转化为关于x的多项式。
-
如果对实数的精度要求非常高,且运算不复杂,可以定义分数类解决。
-
BSGS算法在有多组询问时,可以适当增加步长。
-
使用对数可以把幂变乘,把乘变加,把除变减。例如:,可以变为。
-
在一个数列中,从某个位置开始的所有前缀的gcd,只有种,可以维护。
-
有时,可以对矩阵乘法进行改造,并且,通常改造后会满足结合律。
-
同余不等式可以使用递归求解。
-
有时,可以利用第二类斯特林数把幂变为若干组合数的和。
-
把一个数x拆分成k个数的方案数,可以把x质因数分解,然后对于每种质因数,用组合数插板法计算,再乘到一起。
-
对于异或的随机游走或类似的满足卷积性质的,可以用设FWT结果的方法,把特殊值(起点和终点)与其实际的差设为未知数x。设H为用来调整的差值,每项都是。这样若答案为F,转移为G, 则。那么可以求出,为定值。然后可以用已知值把求出。
可以代替高斯消元。
同时,这类问题也可以转化为集合幂级数。
-
当n足够大时, ≈。
-
转移规律,比较特殊的随机游走(比如树上,网格内)可以不用高斯消元,直接把每个用了相邻的一些来表达,多次递推即可。
-
高斯消元时,如果矩阵有一定规律且非常稀疏,可以优化消元过程。常用于转移依赖有环的DP。
-
对于上述问题,如果能找到较少的变量作为主元,使得其他变量都能用主元表示,就可以只对主元进行高斯消元,优化算法。
-
模意义下的根号采用类似复数的维护,乘法时暴力展开,除法时分母有理化即可。
-
几个积性函数的卷积也是积性函数。因此反演后若答案满足这种形式,可以把n质因数分解,然后把的答案算出来,乘到一起即可。
-
(底数一定时)设表示模p意义下的阶,那么若a,b互质,则。
-
解方程时,若,那么我们可以递推求解,每次把p乘上一个质数并考虑x的变化。复杂度约为
计数
-
遇到用若干个数相加组合成一个数的问题,可以考虑同余最短路(NOIP2017 小凯的疑惑,墨墨的等式)。
-
平方和问题:考虑平方的实际意义 (二维枚举,二维dp)。带组合数的,也可以用类似做法。
-
倍增合并(有时可以使用fft加速合并),有时能比矩阵快速幂少一个m。
-
矩阵乘法两种形式:
- 数列递推,每次生成一个。
- 高维递推优化,每次推进一层。
-
枚举,算贡献(相当于交换求和符号)。
-
两种容斥原理:交集,并集。(都要考虑到)
-
关于匹配的容斥:若有被多次匹配的,就有没被匹配的,按照没被匹配的进行容斥。
-
有些计数类的递推(如:),可以画出转移的图后,(通过扭转等)转移为网格图路径计数问题。
-
网格图有限制的路径计数:
- 只有一个限制(如三角形,j<=i),可以容斥,不合法的可以将起点或终点进行对称。
- 有两个限制(如平行四边形中),还是容斥,但要考虑反复经过分界线的情况。如:A,ABA,B,BAB等应减去。AB,BA,ABAB,BABA以及不进行对称等应加上。
int ans=F(n,n+m); int a=0,b=0;A(a,b);B(a,b); ans=(ans+jisuan1(a,b))%md; a=0;b=0;B(a,b);A(a,b); ans=(ans+jisuan2(a,b))%md; a=0;b=0;B(a,b); ans=(ans-jisuan1(a,b)+md)%md; a=0;b=0;A(a,b); ans=(ans-jisuan2(a,b)+md)%md; -
网格图中两条不相交路径计数,可以用总数减去相交的,相交的就是把交点后面的路径交换。
-
多项式可以放进矩阵中,进行矩阵快速幂。
-
如果多项式的次数始终不是很多,也可以直接用点值法维护,在开始和结束时进行NTT即可。
-
FFT为了防止炸精,可以预处理出单位根,而不是直接乘。
for(int i=0;i<(h>>1);i++) ww[i]=cp(cos(2*pi*lx*i/h),sin(2*pi*lx*i/h)); -
在FFT时若有之类的项,可以转化为,便于FFT。
-
若要求的最值,可以对于每一个x,只看关于它的项,发现是一个二次函数,那么让这个x等于对称轴即可。这样会得出n条方程,高消即可。相当于求偏导。
-
求不相交的路径数目,可以使用LGV引理。注意需要满足把终点交换后路径一定相交。看到类似逆序对奇偶性的问题也可以考虑行列式。
四、博弈
- 只要两个子游戏没有关联了,就可以用sg异或了。
- 翻硬币游戏,只要选的硬币是反转的硬币中编号最大的即可。计算时可以把直接翻转理解为添加。
- 阶梯nim:每次取走若干个放到上一堆中。只要记录奇数位置的异或即可。这个游戏也可以放到树上进行,方法相同。
五、树上问题
-
在一棵树上统计子树信息,如果子树信息不能快速合并,可以采用dsu on tree算法(luogu 雨天的尾巴,回文路径计数)。
-
树链合并(深度和减去相邻lca深度),暴力树链合并,access是均摊的。
-
基环树方法:将环提出,变为森林,对每棵树计算,然后合并。
-
树统计(效率):线段树合并>启发式合并=dsu on tree
-
m个节点的所有lca在O(m)级别,可以用虚树。
-
给定树上若干的点,求最小生成树大小,可以按照dfs序排序后,用总深度减去相邻的lca的深度,再减去所有的lca的深度。
-
建虚树的步骤
int build(vector<int> &sz) { //1. 将点按照dfs序为关键字排序(此处已省略)。 for(int i=0;i<cs;i++) ve[cl[i]].clear(); cl[0]=st[0]=sz[0];cs=tp=1;//2. 清空数组,将第1个点压到栈中。 for(int i=1;i<sz.size();i++) { int u=sz[i],lc=getlca(u,st[tp-1]);//3. 枚举到下一个点u,计算u与栈顶点的最近公共祖先lca while(tp>=2&&de[lc]<=de[st[tp-2]])//4. 假设栈中栈顶下方的点为w(若栈中只有1个点就直跳过这一步),若w点的深度大于等于lca就把v向w连一条边,并且弹掉v,重复此步,否则就到下一步。 { ve[st[tp-2]].push_back(st[tp-1]); tp-=1;lc=getlca(u,st[tp-1]); } if(lc!=st[tp-1])//5. 若lca不是当前的栈顶点,那么就把lca和栈顶点连边 { ve[lc].push_back(st[tp-1]); st[tp-1]=cl[cs++]=lc;//并把栈顶变为lca } st[tp++]=cl[cs++]=u;//6. 最后把u压入栈中 } for(int i=0;i+1<tp;i++)//7. 把栈顶v与栈顶下方的点为w连边,并且把v弹掉,这么做直到栈里只有一个点 ve[st[i]].push_back(st[i+1]); return st[0];//这个点就是虚树的根了 //为了方便,有时把1也加进去。 } -
长链剖分优化dp时,对于轻儿子直接爆算,重儿子继承后将指针移位,进行+1或-1的调整。比如:
int& F(int u,int i) { if(i>=dep[u]) return z0; return f[lf[u]+i]; } if(son[u]!=-1) { dfs2(son[u],u); lg[u]=lg[son[u]]+1;//指针移动 lf[u]=lf[son[u]]-1;//指针移动 } F(u,0)=1; if(son[u]==-1)return; for(int i=fr[u];i!=-1;i=ne[i]) { if(v[i]==fu||v[i]==son[u]) continue; //进行转移 } -
若要求一段路径上的颜色数,可以考虑每种颜色的贡献:若删除所有这种颜色后,起点和终点不在一个连通块中,则有贡献。
-
树的重心,也是树上到其他点距离之和最小的点,满足其子树大小的最大值最小(不超过一半)。如果有两个重心,则这两个重心连着,且最大子树正好为一半。
-
距离树上某一个点的最远点一定是(任意)直径的一个端点。
-
合并两棵树的直径时,新树的直径端点一定是这两棵树的直径端点(共四个)中的两个。可以分6种情况讨论。
-
换根DP:先进行一次DFS,第二次DFS时维护父树的信息。需要考虑如何快速计算一棵子树挖去它的一个儿子后的DP值。
-
求树上两条路径的交:两条路径(a,b)与(c,d),四个点两两求LCA,得到。再从这四个点中取出深度最大的两个点p1,p2
若p1≠p2,则交为p1到p2;若p1=p2,且p1的深度小于 ca(a,b)或小于lca(c,d)的深度,则无交点,否则只有一个交点p1。 -
要求出树上所有路径/连通块的信息,可以使用点分治,这样,每个路径/连通块都会考虑到,且只需。
-
条路径一定可以覆盖有个叶子的树。
-
如果要对最小生成树进行合并,但合并涉及的节点不多,可以每次以合并可能涉及到的点为关键点建立虚树,边权为链上的最大值,换句话说就是求出首次使关键点联通的边,把他们放到一起求MST。(SDOI2019世界地图)
-
边权值数目较少但数量很多的MST,可以每次加入权值相等的一组边,考虑快速求出联通块个数的变化即可。
-
对于LCT,如果要支持加/删点,维护联通块操作,可以把每个点的父亲也加进去。从而保证复杂度。计算答案时,每个联通块删去最上面的那个点即可。
-
LCT维护子树:就是每个点维护下虚边信息,再维护下splay子树中的虚边信息之和。pushup时修改后者,access和link时修改前者。
-
LCT可以维护带修改的树剖(比如动态DP,zjoi历史),在access时修改即可。但一定要注意细节。
-
对于树上询问涉及的点比较少的问题,可以建立虚树。对于虚树的一条边在原树上对应的链的答案,可以使用倍增等算法求出。
-
一个点到一条路径距离的问题,可以树链剖分,每个节点轻儿子的size之和不会超过nlogn。暴力维护这些点。这样一条重链的答案可以查询它们所有节点的轻儿子,最下面的节点就是单点询问,用线段树维护区间信息即可。但注意空间复杂度为。
六、图论
-
最小生成树更新:只需判断环的最值即可
-
图上的所有MST,满足:
1、对于任意权值的边,所有最小生成树中这个权值的边的数量是一定的(根据克鲁斯卡尔算法即可得出)
2、对于任意正确加边方案,加完小于某权值的所有边后图的连通性是一样的
3、对于相同权值的边,任意顺序都是可以的。 -
边权只有0,1的图的最短路可以用bfs求解。
-
在涉及到连通性,以及最长路等问题要考虑缩点(受欢迎的牛)。
-
欧拉回路构造:出栈时输出+“当前弧优化”
-
三元环枚举:按度数将边定向,大->小,之后暴力枚举即可。
-
2-SAT:若a能推出b,连a->b,连!b->!a。
之后,找scc,若一个变量的两种取值位于同一scc,则无解。
若要构造解,则取两种取值中scc编号较小的。 -
奇环的判断使用黑白染色。
-
给一个图,删边,问连通性,可以把非树边随机一个权值,树边的权值为覆盖它的非树边的权值的异或和。查询时求出是否有异或和为0的子集即可。
-
点权图的最短路,每个点只会被更新一次,这个性质可以用于某些优化。比如。
-
点权都为正数的最小(非零)权闭合子图,可以tarjan,然后考虑出度为0的SCC。
-
边权不超过w的带权图,可以拆边变成不带权的图,方法是把每个点拆成长度为w的链,从链上向其他点连边。总共点数为。(NOI2020D1T1)
-
图中不存在负环,可以等价转化为能构造满足最短路性质的点权。有时在dp中可以使用。(AT5147 [AGC036D] Negative Cycle)
-
维护区间联通性可以使用点减边的方法。加入新边时先全都-1,然后把它的端点作为首次出现对应的区间+1。那么对于树来说,最小值等于1的位置就是连通的。
七、网络流
-
平面图的最小割就是对偶图的最短路(每个面看做一个点,相邻的面看做边)(luogu P2046海拔,luogu 狼抓兔子)。
-
网络流的最小割模型:
- “文理分科”
- “选择+2个具有贡献”
-
在题目涉及到所有点对的最大流/最小割时,可以通过最小割树,将其转化为树链上的最小值。
-
对于二分图完美匹配的判定,可以考虑Hall定理。
-
问题:有n个点,选择每个点有代价,m条关系(x,y,z)表示同时选择x,y有z的收益。使收益-代价最小。
可以使用最小割求解。
首先,假设可以得到所有收益,不付出代价。并用最小割割掉不合法的。
S向每个点连边,边权为代价。每个点向T连边,边权为包括它的收益和的一半。
对于每条关系,到连边权为的双向边。
可以把边权先扩大到2倍。 -
最小割的数学定义,令为一个01变量,我们假设若最后在集合,则,否则
则边对答案的贡献为
则边对答案的贡献为
则边对答案的贡献为
同理,如果我们能把贡献写为以上的形式,则可以用最小割求最优解
比如:有若干个01变量,每个变量取0/1有代价,还有若干关系(x,y,z)表示如果x取1,y取0,有z的代价。要求总代价最小。可以使用最小割。 -
有些网络流问题,可以先建出一个比较简单的图,然后把点,边合并。(猪圈)
-
费用随流量增长速度单调,可以将流量差分,把这条边拆开,每条边的流量为差分后的流量。
-
序列的区间覆盖,树上的祖孙链覆盖,可以考虑网络流。建模方法类似k可重区间集。
-
费用流如果要求某条边必须流满,可以把这条边的费用设为无穷大,之后减去即可。
-
网络流dinic的复杂度可以是的,其中W为边权和。
-
费用流可以消去负环,见此处。
八、数据结构
-
有时,权值线段树可以代替treap,能减小常数和代码量(luogu 郁闷的出纳员)。
-
有时,线段树可以代替splay,方法时记录每个位置是否有元素,查询第k个值时线段树上二分(NOIP2017 列队)。
-
处理区间内出现过的数时,可以求出每个数的后继,然后就变成了区间内大于某数的数(luogu HH的项链)。如果在树上可以使用这种方法
-
某种在线-->离线:建立线段树/树状数组,当某个区间都被加入时,离线处理,要求询问区间分裂后能合并结果(其实这个叫做二进制分组)。
-
很多树形数据结构都可以打标记(线段树,splay,左偏树)。
-
通常的树持久化方法:每次新建一个根。避免持久化的技巧:版本树(离线)。
-
在处理覆盖问题时,可以用并查集维护每个点向后第一个未被覆盖的位置(包括自身),比线段树快,树上覆盖也可以。
-
笛卡尔树:将RMQ变为lca,可以动态维护单调栈,解决RMQ之和等问题。
-
计算最大矩形时,除了单调栈,还可以递归,就是每次找到最小值,并递归它两边的区域。
-
处理异或的问题有一种常用技巧:就是把每个二进制位拆开单独处理,这样只有不同的才会有贡献。可以将异或问题转换为了是否为不同的数。
-
有时,我们的可持久化并查集只需要查询历史版本,不需要在历史版本上修改(例如添加边后,询问之前的连通性)。
这时,我们有一个log的做法。
维护一个只按秩合并,不路径压缩的并查集。
对于每条边,记录它出现的时间,判断连通性找根时,如果它到它的父节点的边出现了,就找父节点的根,否则它就是根。
这样,不路径压缩,边的状态只有两种,存在/不存在,若存在就是唯一的。 -
线段树合并,通常用在树上。常常用于树形DP转移时对于某一位取或的优化。
需要满足的条件:在合并时,对于一棵空树,可以直接return或在另一棵树上打标记。 -
看到RMQ之和的问题,可以考虑单调栈,或者每次找RMQ并分治两边。
-
只进行加的高精,有时可以使用线段树维护:加法时,在线段树上二分进行进位。比较时,使用哈希找lcp进行比较(要注意从高位到低位)。并且,可以可持久化。
-
二维线段树通常使用动态开点,x树的每个节点都保存它的y树的根。
-
主席树,二维线段树等数据结构如果要区间修改,通常使用标记永久化(要求标记之间没有顺序要求)。
-
trie字典树支持删除,只要额外维护子树大小即可。
-
标记永久化可以解决一些其它问题,比如:有一棵树,单点修改,查询一个点到根的路径上与x异或的最大值。这个可以做到时间,空间。
-
启发式合并,启发式分裂,有时可以做到log。
-
序列中最大的按位与,只需要取前个数,两两暴力判断即可。扩展一下,取个数的最大and,只需要考虑前大的数即可。
-
主席树可以卡空间:如果每次版本之间有多次修改(比如树剖),可以用全局变量记录哪个点之后都是目前新建的点。这样遇到这类点就不用再次新建节点了。可以省大量空间。
-
主元素:维护一个当前值,以及次数,每次读入一个数,若相同次数加一,否则减一。若次数小于0就把维护的数变为这个数。
这个方法可以拓展,即维护多个出现次数最多的数。也可以放到线段树上。 -
动态维护标号(即支持插入删除并维护相对排名,要求O(1)查询)可以使用替罪羊树:每个节点维护一个区间,那么这个节点的标号为,左子节点区间为,右子节点区间为。不平衡时重构在保证复杂度的同时,也能保证深度不会太大,从而避免精度问题。
-
一切涉及到区间答案,区间转移,区间连边等问题都可以考虑线段树。
-
如果涉及到求一段前缀的答案并且不方便快速合并,可以求出个前缀的答案,每次再暴力加入剩下的的个点即可。
九、几何
-
平面分治,可以用于平面上的最近距离等问题(最近点对,最小周长三角形)。只要先把x排序,分治时把y排序,用双指针扫描即可。
-
叉积好像是满足分配率的。可以拆开预处理。例题
-
叉积实现极角排序:
int xix(SVe a) { if(a.y<0||(a.y==0&&a.x<0)) return 0; return 1; } int cmpj(SVe a,SVe b) { int xa=xix(a),xb=xix(b); if(xa!=xb)return xa-xb; return cross(a,b); } -
一堆线段求x坐标最小的交点,可以按照x坐标扫描线。用维护线段对应一坐标的大小关系,最近的交点一定是中相邻的两条。
十、其它
算法设计
-
生成匹配的括号序列,只需模拟一个栈,记录栈中的括号数即可(CF1015F,CF508E)。
-
求第k小值(k不大),可以采用A*算法,要保证每种状态都能被扩展出,且扩展出的状态非递减(luogu 超级钢琴,K短路,OVOO)。
-
离线处理以及强制在线:
- 离线处理可以把询问排序,并按照顺序求解。强制在线可以全部处理后可持久化(NOI2018 归程)。
- 离线处理可以倒推。
- 离线处理可以得出每种操作的时间序(loj121 动态图的连通性)。
-
当处理一个要求整体满足的问题时,可以只考虑局部,当所有的局部都满足时,整体就满足了(luogu 双栈排序,NOI2018 冒泡排序)。
-
第k小问题的计数可以用容斥 (秘密袭击),就是说:
x成为第k小需要满足两个条件:的数目小于k,的数目大于等于k。
可以用满足1的减去满足1且不满足2的。
显然,不满足2,就一定满足1。
因此,用“的数目小于k”减去“的数目小于k”即可。 -
meet-in-the-middle 算法
应用:BSGS优化,分别以1,平方根为步长,进行预处理,这样,任意一个数都能用处理好的两个数之和来表示。
-
易忘的:
线段树合并
分块,分类
差分约束
预处理
线段树分治,线段树建图,线段树扫描线
2-SAT
bitset优化 -
看到方差可以考虑推式子,转化为平方和-平均数×总和。
-
排列的三维偏序数,可以容斥。答案为。F为二位偏序。
-
判断两种状态能否到达时,若状态的转移有单方向性,可以求出两个状态按照方向转以后到达的最终状态,判断是否相等。(其实就是状态的转移是树形的)。
-
正难则反,可以把问题反过来(比如:让求字符串中是否有不相等的距离为k的两个位置,由于字符串算法大多是求匹配的,所以可以反过来,看是否都相等)。
-
坐标转化:曼哈顿距离是∆ x与∆ y之和,切比雪夫距离是∆ x与∆ y的最大值。
-
考虑一个问题时,可以考虑特殊情况的解法(比如树上问题,可以先考虑链,菊花的情况;基环树,可以先考虑树上的情况)。
-
如果网络流的建图比较简单,可以考虑模拟网络流优化(数据结构实现增广),或堆模拟反悔操作
-
分类考虑:一部分满足种类数小(预处理),一部分计算快,可以分类求(通常平方根为界,但实际上有偏差)。
-
如果题目中要求最后一个,即max,可以使用min-max容斥变为求max,即第一个。
-
树形结构上可以打各种各样的标记。( [BJOI2016]IP地址 )。
-
若对于题目,可以把答案转化为每个点的出(或入)边仅有一条,就可以变为基环树。例:给每条边定向,使得所有边的入点不重复。
-
巧妙使用DFS,可以优化算法。例如在有向图中,判断一条边(a,b)能否从a不经过这条边到达b,可以枚举a,然后把a的出边顺序,逆序分别dfs一次,并记录每个点第一次被dfs时走的是哪条出边,若b点满足有一次dfs中b的标记不是这条边,那么存在。
-
看到把集合分为两组的问题,可以考虑最小割(S,T集合),也可以考虑2-SAT。
-
时光倒流是较为常用的一种技巧。可以把删除变为添加。
-
绝对值小于某数这样的式子可以把绝对值拆开变成两个式子。CTSC2017 网络
-
欧拉定理:。在算联通块个数的问题上可以只算出点,边,面三个即可。
算法优化
-
传有数组的结构体要尽量用引用。
-
模数要用define或const!!!!会快些
-
在枚举子集时,若要遍历其中的元素,可以采用如下方法,会快些:
for(int i=0,j=1;i<n;i++,j=(j<<1)) lg[j]=i; //…… for(int i=0;i<(1<<n);i++) { for(int t=i;t>0;t^=t&(-t)) { int k=lg[t&(-t)]; //…… } } -
FWT的一个小技巧:此处
-
Hash挂链通常比map快,快很多,但要注意hash的方法。
-
在使用枚举+二分时,可以把枚举的顺序打乱,并在二分前先判断当前的最优解是否可行,这样可以把二分的次数降到期望。
-
在优化算法时,可以考虑把若干次相似的操作合并成一次进行。
-
在图中路径计数使用矩阵快速幂时,如果这个图时DAG,可以按照拓扑序之进行三角的枚举,从而把常数变为。
-
若矩阵快速幂复杂度太高,可以考虑使用BM求出前几项递推式,进行快速递推。
-
带修改的二维偏序的枚举,可以做到,方法是按照第一维建立线段树,维护第二维的最值。在枚举时dfs线段树,根据这个最值判断。例题
-
若,则,有时可以利用这个性质优化算法。
-
sort通常比qsort快。尤其是在对较小数组多次排序时。
-
取模优化有时候是有用的。可以用这个:
x+=(x>>31)&md;//x为负数则加上md
三、一些公式
组合数

二项式反演

min/max容斥扩展
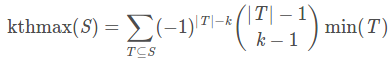
单位根反演
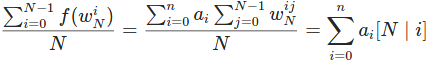




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现