模拟赛 斯特林数计数 题解（拉格朗日插值）

题目大意：
求

答案对\(10^9 + 7\)取模。

首先，我们发现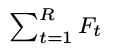这个东西出现了很多次。
设R=。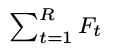

R可以矩阵乘法求。
根据斯特林数的

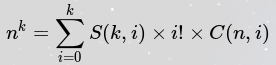
原式可化为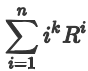
设所求为\(f_k(N)\)。

对于\(R=1\)的情况,自然数幂求和即可。\(O(k+logn)\)。

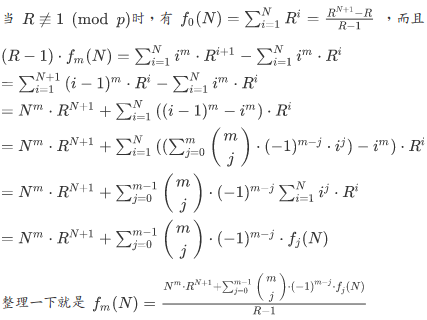
所以，

由上述暴力展开的情况可以发现，存在一个关于\(N\)的\(m\)次多项式\(F_m(N)\)，
使得\(f_m(N)=F_m(N)R^{N+1}-F_m(0)R\)，利用上述的展开方式也可归纳证明这个结论。

所以，求出\(F_m(N)\)即可，由于它是\(m\)次多项式，所以，求出\(F_m(0)到F_m(m)\)即可插值求出\(F_m(N)\)。
因为\(f_m(N)-f_m(N-1)=F_m(N)R^{N+1}-F_m(N-1)R^N=N^m R^N\)，所以\(F_m(N)R-F_m(N-1)=N^m\)，
即\(F_m(N)=\frac{N^m+F_m(N-1)}{R}\)。
设\(F_m(0)=x\)，那么\(F_m(i)\)就能表示为\(k_ix+b_i\)的形式。
那么，我们只要再找一条\(F_m\)的等量关系即可求出。

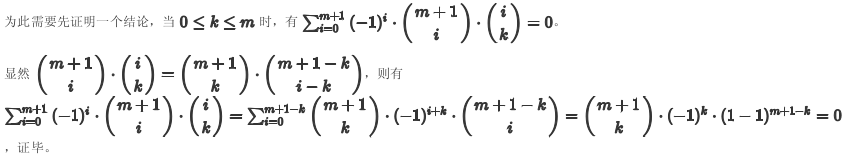
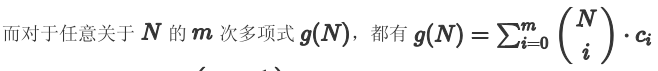
代入到上一条式子，即可得出

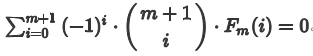
（其实就是说m次多项式的m+1次差分等于0，这条式子可以保证\(F_m\)形成一个m次多项式）。
也可以这样理解：我们用\(m+1\)个点(0~m)就能确定一个多项式，但要保证确定的多项式代入\(m+1\)的值是正确的。
通过拉格朗日插值也能得出这条式子。

这样，我们就能求出\(F_m(0)到F_m(m)\)，再通过插值，即可求出\(F_m(N)\)，进而求出答案。

通过线性筛,可以在计算质数\(p\)的\(p^m\)后线性地算出所有正整数\(x\)的\(x^m\)。
时间复杂度为\(O(\frac{m}{ln(m)}*log_2(m))=O(m)\)。

总时间复杂度\(O(k+logn)\)。

代码：

#include <stdio.h>
#define md 1000000007
#define ll long long
int ny[200010],jc[200010],jn[200010];
int C(int n,int m)
{
	return 1ll*jc[n]*jn[m]%md*jn[n-m]%md;
}
int ksm(int a,int b)
{
	int jg=1;
	while(b>0)
	{
		if(b&1)
			jg=1ll*jg*a%md;
		a=1ll*a*a%md;
		b=(b>>1);
	}
	return jg;
}
int getfib(ll x)
{
	int a=1,b=0,c=0,d=1,w[70],s=0;
	while(x>0)
	{
		w[s++]=x%2;
		x/=2;
	}
	for(int i=s-1;i>=0;i--)
	{
		int bc=1ll*b*c%md,ad=(a+d)%md;
		b=1ll*b*ad%md;c=1ll*c*ad%md;
		a=(1ll*a*a+bc)%md;
		d=(1ll*d*d+bc)%md;
		if(w[i])
		{
			int ta=a,tc=c;
			a=(a+b)%md;
			c=(c+d)%md;
			b=ta;d=tc;
		}
	}
	return c;
}
int qz[200010],hz[200010];
int jisuan(int sz[200010],int n,ll x)
{
	for(int i=0;i<=n;i++)
	{
		if(i==0)qz[i]=1;
		else qz[i]=qz[i-1];
		qz[i]=1ll*qz[i]*(x%md-i+md)%md;
	}
	for(int i=n;i>=0;i--)
	{
		if(i==n)hz[i]=1;
		else hz[i]=hz[i+1];
		hz[i]=1ll*hz[i]*(x%md-i+md)%md;
	}
	int ans=0;
	for(int i=0;i<=n;i++)
	{
		int l=1ll*jn[i]*jn[n-i]%md;
		if(i>0)l=1ll*l*qz[i-1]%md;
		if(i<n)l=1ll*l*hz[i+1]%md;
		if((n-i)%2==1)
			l=1ll*l*(md-1)%md;
		ans=(ans+1ll*l*sz[i])%md;
	}
	return ans;
}
int mi[200010],k[200010],b[200010],S[200010],F[200010];
int sa[200010],ss[200010],sl=0;
void yucl(int x,int m)
{
	mi[1]=1;
	for(int i=2;i<=x;i++)
	{
		if(!sa[i])
		{
			ss[sl++]=i;
			mi[i]=ksm(i,m);
		}
		for(int j=0;j<sl;j++)
		{
			if(1ll*i*ss[j]>x)
				break;
			sa[i*ss[j]]=true;
			mi[i*ss[j]]=1ll*mi[i]*mi[ss[j]]%md;
			if(i%ss[j]==0)break;
		}
	}
}
int main()
{
	freopen("c.in","r",stdin);
	freopen("c.out","w",stdout);
	ll n,r;int K;
	scanf("%lld%lld%d",&n,&r,&K);
	ny[1]=jc[0]=jn[0]=1;
	for(int i=2;i<=K+1;i++)
		ny[i]=1ll*(md-md/i)*ny[md%i]%md;
	for(int i=1;i<=K+1;i++)
	{
		jc[i]=1ll*jc[i-1]*i%md;
		jn[i]=1ll*jn[i-1]*ny[i]%md;
	}
	yucl(K+1,K);
	int R=(getfib(r+2)-1+md)%md;
	if(R==1)
	{
		for(int i=1;i<=K+1;i++)
			mi[i]=(mi[i]+mi[i-1])%md;
		printf("%d",jisuan(mi,K+1,n));
	}
	else
	{
		int rn=ksm(R,md-2);
		k[0]=1;b[0]=0;
		for(int i=1;i<=K+1;i++)
		{
			k[i]=1ll*k[i-1]*rn%md;
			b[i]=1ll*(b[i-1]+mi[i])*rn%md;
		}
		int hk=0,hb=0;
		for(int i=0;i<=K+1;i++)
		{
			int t=C(K+1,i);
			if(i%2==1)
				t=1ll*t*(md-1)%md;
			hk=(hk+1ll*t*k[i])%md;
			hb=(hb+1ll*t*b[i])%md;
		}
		F[0]=1ll*(md-hb)*ksm(hk,md-2)%md;
		for(int i=1;i<=K;i++)
			F[i]=(1ll*k[i]*F[0]+b[i])%md;
		int fn=jisuan(F,K,n);
		int ans=1ll*fn*ksm(R,(n+1)%(md-1))%md;
		ans=(ans-1ll*F[0]*R%md+md)%md;
		printf("%d\n",ans);
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}