[CQOI2017]老C的方块
题意:
老C是个程序员。
游戏被限定在一个由小方格排成的R行C列网格上,有些相邻的小方格之间的公共边比较特殊。
特殊的公共边排列得有很强的规律,下图所示是一个R=C=8的网格,蓝色标注的边是特殊边。
如果网格的规模更大,我们可以用同样的方法找出所有的特殊边。
网格的每个小方格刚好可以放入一个小方块,在游戏的一开始,有些小方格已经放上了小方块,另外的小方格没有放。
有一些小方块排列成了它讨厌的形状(特殊边的位置也要如图中所示),即使是经过任意次旋转、翻转。
为了防止弃疗,老C决定移除一些格子里小方块,使得剩下的小方块不能构成它讨厌的形状。
但是游戏里每移除一个方块都是要花费一些金币的,老C当然希望尽可能少的使用游戏里的金币。
题解:
网络流。
首先,观察题目中的图
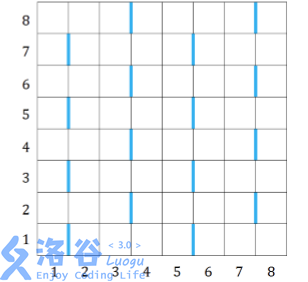
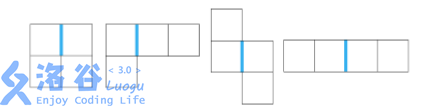
可以发现,蓝边周围的两个点,要么破坏一个,要么破坏周围的。而周围的都满足距离为奇数。
看到这个条件,又是网格图,可以黑白染色。
这样,周围的点的颜色一定不同,可以建二分图,使用最小割。
然而,有一个“要么破坏一个,要么破坏周围的。”的要求,即“或”的限制。
在最小割中,“或”就是串联,这个割掉一个就破坏了路径。
而周围的破坏所有才行,即“与”,就是并联。
把中间两个点连min的边,周围的点并联,再串联到中间的点上。
如图
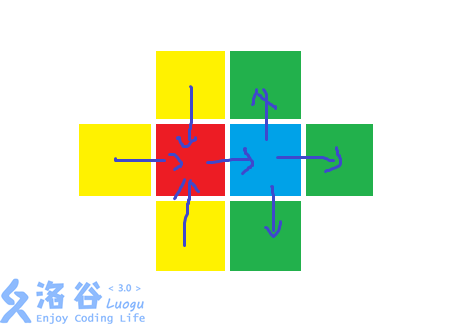
最小割即可,跑不满,所以能过。
注意建图细节。
代码:
#include <stdio.h>
#include <map>
using namespace std;
#define N 200010
#define M 1000010
#define min(a, b) a < b ? a: b
#define ll long long
int fr[N],ne[M],v[M],w[M],bs = 0;
void add(int a, int b, int c) {
v[bs] = b;
w[bs] = c;
ne[bs] = fr[a];
fr[a] = bs++;
}
int dl[N],jl[N],dy[N],S,T,n,inf = 2000000000;
bool bk[N];
bool bfs() {
for (int i = 1; i <= n; i++) {
bk[i] = false;
jl[i] = inf;
}
int he = 0, ta = 1;
dl[he] = S;
bk[S] = true;
jl[S] = 0;
while (he < ta) {
int u = dl[he];
for (int i = fr[u]; i != -1; i = ne[i]) {
if (w[i] > 0 && !bk[v[i]]) {
bk[v[i]] = true;
jl[v[i]] = jl[u] + 1;
dl[ta++] = v[i];
}
}
he += 1;
}
return jl[T] < inf;
}
int dfs(int u, int z) {
if (u == T) return z;
for (int & i = dy[u]; i != -1; i = ne[i]) {
if (w[i] > 0 && jl[v[i]] == jl[u] + 1) {
int rt = dfs(v[i], min(w[i], z));
if (rt != -1) {
w[i] -= rt;
w[i ^ 1] += rt;
return rt;
}
}
}
return - 1;
}
int dinic() {
int jg = 0;
while (bfs()) {
for (int i = 1; i <= n; i++) dy[i] = fr[i];
while (1) {
int rt = dfs(S, inf);
if (rt == -1) break;
jg += rt;
}
}
return jg;
}
void addb(int a, int b, int c) {
add(a, b, c);
add(b, a, 0);
}
int x[100010],y[100010],z[100010],fx[6][2] = {-1,0,1,0,0,-1,-1,1,1,1,0,2},r,c;
map < ll,int > mp;
bool check(int x, int y) {
if (x % 2 == 1) return y % 4 == 1;
else return y % 4 == 3;
}
int getwz(int x, int y) {
if (x <= 0 || x > r || y <= 0 || y > c) return - 1;
ll t = 1ll * x * c + y;
if (mp.count(t) == 0) return - 1;
return mp[t];
}
void link(int z1, int z2, int a, int b) {
addb(a, b, min(z[z1], z[z2]));
for (int s = 0; s < 6; s++) {
int tx = x[z1] + fx[s][0],
ty = y[z1] + fx[s][1];
int wz = getwz(tx, ty);
if (wz == -1) continue;
if ((tx + ty) % 2 == 0) addb(wz + 3, a, inf);
else addb(b, wz + 3, inf);
}
}
int main() {
int m;
scanf("%d%d%d", &c, &r, &m);
for (int i = 0; i < m; i++) scanf("%d%d%d", &y[i], &x[i], &z[i]);
S = 1; T = 2; n = m + 2;
for (int i = 1; i <= n; i++) fr[i] = -1;
for (int i = 0; i < m; i++) {
if ((x[i] + y[i]) % 2 == 0) addb(S, i + 3, z[i]);
else addb(i + 3, T, z[i]);
mp[1ll * x[i] * c + y[i]] = i;
}
for (int i = 0; i < m; i++) {
int t;
if (check(x[i], y[i]) && (t = getwz(x[i], y[i] + 1)) != -1) {
fr[n + 1] = fr[n + 2] = -1;
link(i, t, n + 1, n + 2);
n += 2;
}
}
printf("%d", dinic());
return 0;
}



